二分查找知识（二）

3. 二分查找细节

从上篇文章的例子中我们了解了二分查找的思路和具体代码。但是真正在解决二分查找题目的时候还需要考虑更多细节。比如说以下几个问题：

1. 区间的开闭问题：区间应该是左闭右闭区间 $[left, right]$，还是左闭右开区间 $[left, right)$？
2. $mid$ 的取值问题：$mid = \lfloor \frac{left + right}{2} \rfloor$，还是 $mid = \lfloor \frac{left + right + 1}{2} \rfloor$？
3. 出界条件的判断：$left \le right$，还是 $left < right$？
4. 搜索区间范围的选择：$left = mid + 1$、$right = mid - 1$、 $left = mid$、$right = mid$ 应该怎么写？

下面依次进行讲解。

3.1 区间的开闭问题

左闭右闭区间、左闭右开区间指的是初始待查找区间的范围。

• 左闭右闭区间：初始化时，$left = 0$，$right = len(nums) - 1$。

  • $left$ 为数组第一个元素位置，$right$ 为数组最后一个元素位置。
  • 区间 $[left, right]$ 左右边界上的点都能取到。

• 左闭右开区间：初始化时，$left = 0$，$right = len(nums)$。

  • $left$ 为数组第一个元素位置，$right$ 为数组最后一个元素的下一个位置。
  • 区间 $[left, right)$ 左边界点能取到，而右边界上的点不能取到。

关于二分查找算法的左闭右闭区间、左闭右开区间，其实在网上都有对应的代码。但是相对来说，左闭右开区间这种写法在解决问题的过程中，会使得问题变得复杂，需要考虑的情况更多，所以不建议使用左闭右开区间这种写法，而是建议：全部使用「左闭右闭区间」这种写法。

3.2 $mid$ 的取值问题

在二分查找的实际问题中，最常见的 $mid$ 取值公式有两个：

1. mid = (left + right) // 2。
2. mid = (left + right + 1) // 2 。

式子中 // 所代表的含义是「中间数向下取整」。当待查找区间中的元素个数为奇数个，使用这两种取值公式都能取到中间元素的下标位置。

而当待查找区间中的元素个数为偶数时，使用 mid = (left + right) // 2 式子我们能取到中间靠左边元素的下标位置，使用 mid = (left + right + 1) // 2 式子我们能取到中间靠右边元素的下标位置。

mid 取值问题 1

mid 取值问题 2

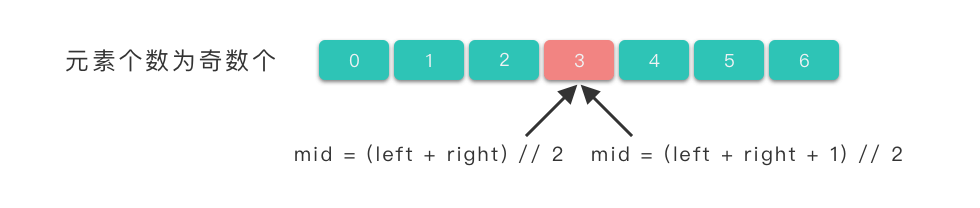
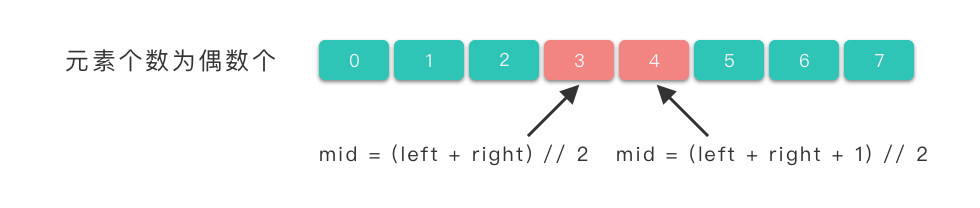
把这两个公式分别代入到 704. 二分查找 的代码中试一试，发现都能通过题目评测。这是为什么呢？

因为二分查找算法的思路是：根据每次选择中间位置上的数值来决定下一次在哪个区间查找元素。每一次选择的元素位置可以是中间位置，但并不是一定非得是区间中间位置元素，靠左一些、靠右一些、甚至区间三分之一、五分之一处等等，都是可以的。比如说 mid = (left + right) * 1 // 5 也是可以的。

但一般来说，取区间中间位置在平均意义下所达到的效果最好。同时这样写最简单。而对于这两个取值公式，大多数时候是选择第一个公式。不过，有些情况下，是需要考虑第二个公式的，我们会在「4.2 排除法」中进行讲解。

除了上面提到的这两种写法，我们还经常能看到下面两个公式：

1. mid = left + (right - left) // 2。
2. mid = left + (right - left + 1) // 2。

这两个公式其实分别等同于之前两个公式，可以看做是之前两个公式的另一种写法。这种写法能够防止整型溢出问题（Python 语言中整型不会溢出，其他语言可能会有整型溢出问题）。

在 $left + right$ 的数据量不会超过整型变量最大值时，这两种写法都没有问题。在 $left + right$ 的数据量可能会超过整型变量最大值时，最好使用第二种写法。所以，为了统一和简化二分查找算法的写法，建议统一写成第二种写法：

1. mid = left + (right - left) // 2。
2. mid = left + (right - left + 1) // 2。

3.3 出界条件的判断

二分查找算法的写法中，while 语句出界判断条件通常有两种：

1. left <= right。
2. left < right。

我们究竟应该使用哪一种写法呢？

我们先来判断一下导致 while 语句出界的条件是什么。

1. 如果判断语句为 left <= right，并且查找的元素不在有序数组中，则 while 语句的出界条件是 left > right，也就是 left == right + 1，写成区间形式就是 $[right + 1, right]$，此时待查找区间为空，待查找区间中没有元素存在，此时终止循环时，可以直接返回 $-1$。
   • 比如说区间 $[3, 2]$， 此时左边界大于右边界，直接终止循环，返回 $-1$ 即可。
2. 如果判断语句为left < right，并且查找的元素不在有序数组中，则 while 语句出界条件是 left == right，写成区间形式就是 $[right, right]$。此时区间不为空，待查找区间还有一个元素存在，我们并不能确定查找的元素不在这个区间中，此时终止循环时，如果直接返回 $-1$ 就是错误的。
   • 比如说区间 $[2, 2]$，如果元素 $nums[2]$ 刚好就是目标元素 $target$，此时终止循环，返回 $-1$ 就漏掉了这个元素。

但是如果我们还是想要使用 left < right 的话，怎么办？

可以在出界之后增加一层判断，判断 $left$ 所指向位置是否等于目标元素，如果是的话就返回 $left$，如果不是的话返回 $-1$。即：

# ...
    while left < right:
        # ...
    return left if nums[left] == target else -1

此外，while 判断语句用 left < right 有一个好处，就是在跳出循环的时候，一定是 left == right，我们就不用判断此时应该返回 $left$ 还是 $right$ 了。

3.4 搜索区间范围的选择

在进行区间范围选择的时候，通常有三种写法：

1. left = mid + 1，right = mid - 1。
2. left = mid + 1 ，right = mid。
3. left = mid，right = mid - 1。

我们到底应该如何确定搜索区间范围呢？

这是二分查找的一个难点，写错了很容易造成死循环，或者得不到正确结果。

这其实跟二分查找算法的两种不同思路和三种写法有关。

• 思路 1：「直接法」—— 在循环体中找到元素后直接返回结果。
• 思路 2：「排除法」—— 在循环体中排除目标元素一定不存在区间。

接下来我们具体讲解下这两种思路。

4. 二分查找两种思路

4.1 直接法

直接法思想：一旦我们在循环体中找到元素就直接返回结果。

这种思路比较简单，其实我们在上篇 「2. 简单二分查找 - 704. 二分查找」 中就已经用过了。这里再看一下思路和代码：

思路 1：直接法

1. 设定左右边界为数组两端，即 $left = 0$，$right = len(nums) - 1$，代表待查找区间为 $[left, right]$（左闭右闭区间）。
2. 取两个节点中心位置 $mid$，先比较中心位置值 $nums[mid]$ 与目标值 $target$ 的大小。
   1. 如果 $target == nums[mid]$，则返回中心位置。
   2. 如果 $target > nums[mid]$，则将左节点设置为 $mid + 1$，然后继续在右区间 $[mid + 1, right]$ 搜索。
   3. 如果 $target < nums[mid]$，则将右节点设置为 $mid - 1$，然后继续在左区间 $[left, mid - 1]$ 搜索。
3. 如果左边界大于右边界，查找范围缩小为空，说明目标元素不存在，此时返回 $-1$。

思路 1：代码

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        # 在区间 [left, right] 内查找 target
        while left <= right:
            # 取区间中间节点
            mid = left + (right - left) // 2
            # 如果找到目标值，则直接范围中心位置
            if nums[mid] == target:
                return mid
            # 如果 nums[mid] 小于目标值，则在 [mid + 1, right] 中继续搜索
            elif nums[mid] < target:
                left = mid + 1
            # 如果 nums[mid] 大于目标值，则在 [left, mid - 1] 中继续搜索
            else:
                right = mid - 1
        # 未搜索到元素，返回 -1
        return -1

思路 1：细节

• 这种思路是在一旦循环体中找到元素就直接返回。
• 循环可以继续的条件是 left <= right。
• 如果一旦退出循环，则说明这个区间内一定不存在目标元素。

4.2 排除法

排除法思想：在循环体中排除目标元素一定不存在区间。

思路 2：排除法

1. 设定左右边界为数组两端，即 $left = 0$，$right = len(nums) - 1$，代表待查找区间为 $[left, right]$（左闭右闭区间）。
2. 取两个节点中心位置 $mid$，比较目标元素和中间元素的大小，先将目标元素一定不存在的区间排除。
3. 然后在剩余区间继续查找元素，继续根据条件排除目标元素一定不存在的区间。
4. 直到区间中只剩下最后一个元素，然后再判断这个元素是否是目标元素。

根据排除法的思路，我们可以写出来两种代码。

思路 2：代码 1

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        # 在区间 [left, right] 内查找 target
        while left < right:
            # 取区间中间节点
            mid = left + (right - left) // 2
            # nums[mid] 小于目标值，排除掉不可能区间 [left, mid]，在 [mid + 1, right] 中继续搜索
            if nums[mid] < target:
                left = mid + 1 
            # nums[mid] 大于等于目标值，目标元素可能在 [left, mid] 中，在 [left, mid] 中继续搜索
            else:
                right = mid
        # 判断区间剩余元素是否为目标元素，不是则返回 -1
        return left if nums[left] == target else -1

思路 2：代码 2

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        # 在区间 [left, right] 内查找 target
        while left < right:
            # 取区间中间节点
            mid = left + (right - left + 1) // 2
            # nums[mid] 大于目标值，排除掉不可能区间 [mid, right]，在 [left, mid - 1] 中继续搜索
            if nums[mid] > target:
                right = mid - 1 
            # nums[mid] 小于等于目标值，目标元素可能在 [mid, right] 中，在 [mid, right] 中继续搜索
            else:
                left = mid
        # 判断区间剩余元素是否为目标元素，不是则返回 -1
        return left if nums[left] == target else -1

思路 2：细节

• 判断语句是 left < right。这样在退出循环时，一定有left == right 成立，就不用判断应该返回 $left$ 还是 $right$ 了。此时只需要判断 $nums[left]$ 是否为目标元素即可。

• 在循环体中，比较目标元素和中间元素的大小之后，优先将目标元素一定不存在的区间排除，然后再从剩余区间中确定下一次查找区间的范围。

• 在将目标元素一定不存在的区间排除之后，它的对立面（即 else 部分）一般就不需要再考虑区间范围了，直接取上一个区间的相反区间。如果上一个区间是 $[mid + 1, right]$，那么相反区间就是 $[left, mid]$。如果上一个区间是 $[left, mid - 1]$，那么相反区间就是 $[mid, right]$。

• 为了避免陷入死循环，当区分被划分为 $[left, mid - 1]$ 与 $[mid, right]$ 两部分时，$mid$ 取值要向上取整。即 mid = left + (right - left + 1) // 2。因为如果当区间中只剩下两个元素时（此时 right = left + 1），一旦进入 left = mid 分支，区间就不会再缩小了，下一次循环的查找区间还是 $[left, right]$，就陷入了死循环。

  • 比如左边界 $left = 5$，右边界 $right = 6$，此时查找区间为 $[5, 6]$，$mid = 5 + (6 - 5) // 2 = 5$，如果进入 $left = mid$ 分支，那么下次查找区间仍为 $[5, 6]$，区间不再缩小，陷入死循环。
  • 这种情况下，$mid$ 应该向上取整，$mid = 5 + (6 - 5 + 1) // 2 = 6$，如果进入 $left = mid$ 分支，则下次查找区间为 $[6, 6]$。

• 关于边界设置可以记忆为：只要看到 left = mid 就向上取整。或者记为：

  • left = mid + 1、right = mid 和 mid = left + (right - left) // 2 一定是配对出现的。
  • right = mid - 1、left = mid 和 mid = left + (right - left + 1) // 2 一定是配对出现的。

4.3 两种思路适用范围

• 直接法：因为判断语句是 left <= right，有时候要考虑返回是 $left$ 还是 $right$。循环体内有 3 个分支，并且一定有一个分支用于退出循环或者直接返回。这种思路适合解决简单题目。即要查找的元素性质简单，数组中都是非重复元素，且 ==、>、< 的情况非常好写的时候。
• 排除法：更加符合二分查找算法的减治思想。每次排除目标元素一定不存在的区间，达到减少问题规模的效果。然后在可能存在的区间内继续查找目标元素。这种思路适合解决复杂题目。比如查找一个数组里可能不存在的元素，找边界问题，可以使用这种思路。

参考资料

• 【博文】Learning-Algorithms-with-Leetcode - 第 3.1 节 二分查找算法
• 【博文】二分法的细节加细节 你真的应该搞懂！！！_小马的博客
• 【课程】零起步学算法 - LeetBook - 二分查找的基本思想：减而治之
• 【题解】二分查找算法细节详解，顺便写了首诗 - LeetCode