图的最小生成树

1. 最小生成树的定义

在了解「最小生成树」之前，我们需要要先理解 「生成树」的概念。

生成树（Spanning Tree）：如果无向连通图 G 的一个子图是一棵包含图 G 所有顶点的树，则称该子图为 G 的生成树。生成树是连通图的包含图中的所有顶点的极小连通子图。图的生成树不惟一。从不同的顶点出发进行遍历，可以得到不同的生成树。

换句话说，生成树是原图 G 的一个子图，它包含了原图 G 的所有顶点，并且通过选择图中一部分边连接这些顶点，使得子图中没有环。

生成树有以下特点：

1. 包含所有顶点：生成树中包含了原图的所有顶点。
2. 连通性：生成树是原图的一个连通子图，意味着任意两个顶点之间都存在一条路径。
3. 无环图：生成树一个无环图。
4. 边数最少：在包含所有顶点的情况下，生成树的边数最少，其边数为顶点数减 $1$。

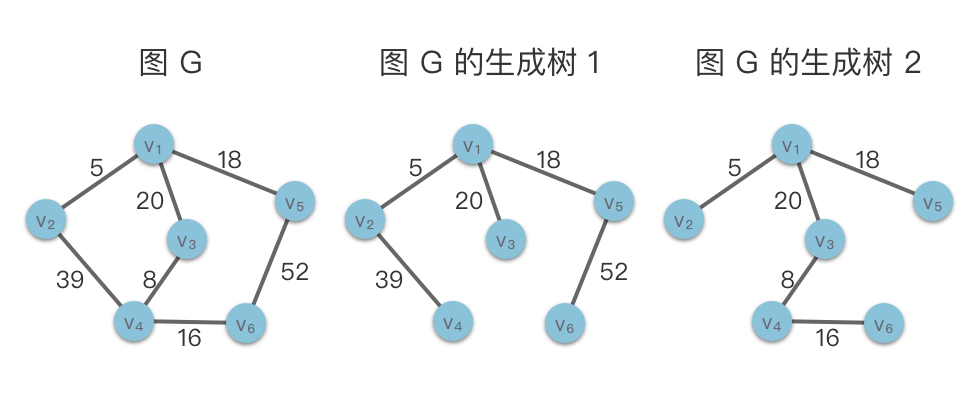
如上图所示，左侧图 $G$ 是包含 $v_1…v_6$ 共 $6$ 个顶点 $7$ 条边在内的有权图。右侧是图 $G$ 的两个生成树，两者都包含了 $6$ 个顶点 $5$ 条边。

最小生成树（Minimum Spanning Tree）：无向连通图 G 的所有生成树中，边的权值之和最小的生成树，被称为最小生成树。

最小生成树除了包含生成树的特点之外，还具有一个特点。

1. 边的权值之和最小：在包含所有顶点的情况下，最小生成树的边的权重之和是所有可能的生成树中最小的。

如上图所示，左侧图 $G$ 是包含 $v_1…v_6$ 共 $6$ 个顶点 $7$ 条边在内的有权图。右侧是图 $G$ 的最小生成树，包含了 $6$ 个顶点 $5$ 条边，并且所有边的权值和最小。

为了找到无向图的最小生成树，常用的算法有「Prim 算法」和「Kruskal 算法」。

• Prim 算法：从一个起始顶点出发，逐步选择与已经构建的树连接的最短边，直到包含所有顶点为止。
• Kruskal 算法：基于边的排序和并查集数据结构，逐步添加边，并保证所选边不会构成环路，直到构建出最小生成树。

这两个算法都可以帮助我们找到图中的最小生成树，以满足连接所有顶点的要求同时使得总权重最小。

2. Prim 算法

2.1 Prim 算法的算法思想

Prim 算法的算法思想：每次选择最短边来扩展最小生成树，从而保证生成树的总权重最小。算法通过不断扩展小生成树的顶点集合 $MST$，逐步构建出最小生成树。

2.2 Prim 算法的实现步骤

1. 将图 $G$ 中所有的顶点 $V$ 分为两个顶点集合 $V_A$ 和 $V_B$。其中 $V_A$ 为已经加入到最小生成树的顶点集合，$V_B$ 是还未加入生成树的顶点集合。
2. 选择起始顶点 $start$，将其加入到最小生成树的顶点集合 $V_A$ 中。
3. 从 $V_A$ 的顶点集合中选择一个顶点 $u$，然后找到连接顶点 $u$ 与 $V_B$ 之间的边中权重最小的边。
4. 让上一步中找到的顶点和边加入到 $MST$ 中，更新 $MST$ 的顶点集合和边集合。
5. 重复第 $3 \sim 4$ 步，直到 $MST$ 的顶点集合中包含了图中的所有顶点为止。

2.3 Prim 算法的实现代码

class Solution:
    # graph 为图的邻接矩阵，start 为起始顶点
    def Prim(self, graph, start):
        size = len(graph)
        vis = set()
        dist = [float('inf') for _ in range(size)]
    
        ans = 0                             # 最小生成树的边权和
        dist[start] = 0                     # 初始化起始顶点到起始顶点的边权值为 0
    
        for i in range(1, size):            # 初始化起始顶点到其他顶点的边权值
            dist[i] = graph[start][i]
        vis.add(start)                      # 将 start 顶点标记为已访问
    
        for _ in range(size - 1):
            min_dis = float('inf')
            min_dis_pos = -1
            for i in range(size):
                if i not in vis and dist[i] < min_dis:
                    min_dis = dist[i]
                    min_dis_pos = i
            if min_dis_pos == -1:           # 没有顶点可以加入 MST，图 G 不连通
                return -1
            ans += min_dis                  # 将顶点加入 MST，并将边权值加入到答案中
            vis.add(min_dis_pos)
            for i in range(size):
                if i not in vis and dist[i] > graph[min_dis_pos][i]:
                    dist[i] = graph[min_dis_pos][i]
        return ans

points = [[0,0]]
graph = dict()
size = len(points)
for i in range(size):
    x1, y1 = points[i]
    for j in range(size):
        x2, y2 = points[j]
        dist = abs(x2 - x1) + abs(y2 - y1)
        if i not in graph:
            graph[i] = dict()
        if j not in graph:
            graph[j] = dict()
        graph[i][j] = dist
        graph[j][i] = dist
        

print(Solution().Prim(graph))

2.4 Prim 算法复杂度分析

Prim 算法的时间复杂度主要取决于以下几个因素：

1. 初始化阶段：

   • 初始化距离数组和访问数组的时间复杂度为 $O(V)$，其中 $V$ 是图中的顶点数。

2. 主循环阶段：

   • 外层循环需要执行 $V-1$ 次，用于选择 $V-1$ 条边。
   • 每次循环中需要：
     • 找到未访问顶点中距离最小的顶点，时间复杂度为 $O(V)$。
     • 更新相邻顶点的距离，时间复杂度为 $O(V)$。

因此，Prim 算法的总体复杂度为：

• 时间复杂度：$O(V^2)$，其中 $V$ 是图中的顶点数。
• 空间复杂度：$O(V)$，主要用于存储距离数组和访问数组。

3. Kruskal 算法

3.1 Kruskal 算法的算法思想

Kruskal 算法的算法思想：通过依次选择权重最小的边并判断其两个端点是否连接在同一集合中，从而逐步构建最小生成树。这个过程保证了最终生成的树是无环的，并且总权重最小。

在实际实现中，我们通常使用并查集数据结构来管理顶点的集合信息，以便高效地判断两个顶点是否在同一个集合中，以及合并集合。

3.2 Kruskal 算法的实现步骤

1. 将图中所有边按照权重从小到大进行排序。
2. 将每个顶点看做是一个单独集合，即初始时每个顶点自成一个集合。
3. 按照排好序的边顺序，按照权重从小到大，依次遍历每一条边。
4. 对于每条边，检查其连接的两个顶点所属的集合：
   1. 如果两个顶点属于同一个集合，则跳过这条边，以免形成环路。
   2. 如果两个顶点不属于同一个集合，则将这条边加入到最小生成树中，同时合并这两个顶点所属的集合。
5. 重复第 $3 \sim 4$ 步，直到最小生成树中的变数等于所有节点数减 $1$ 为止。

3.3 Kruskal 算法的实现代码

class UnionFind:

    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.count = n

    def find(self, x):
        while x != self.parent[x]:
            self.parent[x] = self.parent[self.parent[x]]
            x = self.parent[x]
        return x

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return

        self.parent[root_x] = root_y
        self.count -= 1

    def is_connected(self, x, y):
        return self.find(x) == self.find(y)
    

class Solution:
    def Kruskal(self, edges, size):
        union_find = UnionFind(size)
        
        edges.sort(key=lambda x: x[2])
        
        res, cnt = 0, 1
        for x, y, dist in edges:
            if union_find.is_connected(x, y):
                continue
            ans += dist
            cnt += 1
            union_find.union(x, y)
            if cnt == size - 1:
                return ans
        return ans
    
    def minCostConnectPoints(self, points: List[List[int]]) -> int:
        size = len(points)
        edges = []
        for i in range(size):
            xi, yi = points[i]
            for j in range(i + 1, size):
                xj, yj = points[j]
                dist = abs(xi - xj) + abs(yi - yj)
                edges.append([i, j, dist])
                
        ans = Solution().Kruskal(edges, size)
        return ans

3.4 Kruskal 算法复杂度分析

Kruskal 算法的时间复杂度主要取决于以下几个因素：

1. 边的排序：对 $E$ 条边进行排序的时间复杂度为 $O(E \log E)$。

2. 并查集操作：

   • 查找操作（find）的时间复杂度为 $O(\alpha(n))$，其中 $\alpha(n)$ 是阿克曼函数的反函数，增长极其缓慢，可以近似认为是常数时间。
   • 合并操作（union）的时间复杂度也是 $O(\alpha(n))$。

3. 遍历边的过程：需要遍历所有边，时间复杂度为 $O(E)$。

因此，Kruskal 算法的总体时间复杂度为：

• 时间复杂度：$O(E \log E)$，其中 $E$ 是图中的边数。
• 空间复杂度：$O(V)$，其中 $V$ 是图中的顶点数，主要用于存储并查集数据结构。