0133. 克隆图

ITCharge大约 4 分钟

0133. 克隆图

标签：深度优先搜索、广度优先搜索、图、哈希表
难度：中等

题目链接

0133. 克隆图 - 力扣

题目大意

描述：以每个节点的邻接列表形式（二维列表）给定一个无向连通图，其中 $adjList[i]$ 表示值为 $i + 1$ 的节点的邻接列表， $adjList[i][j]$ 表示值为 $i + 1$ 的节点与值为 $adjList[i][j]$ 的节点有一条边。

要求：返回该图的深拷贝。

说明：

节点数不超过 $100$ 。
每个节点值 $Node.val$ 都是唯一的， $1 \le Node.val \le 100$ 。
无向图是一个简单图，这意味着图中没有重复的边，也没有自环。
由于图是无向的，如果节点 $p$ 是节点 $q$ 的邻居，那么节点 $q$ 也必须是节点 $p$ 的邻居。
图是连通图，你可以从给定节点访问到所有节点。

示例：

示例 1：

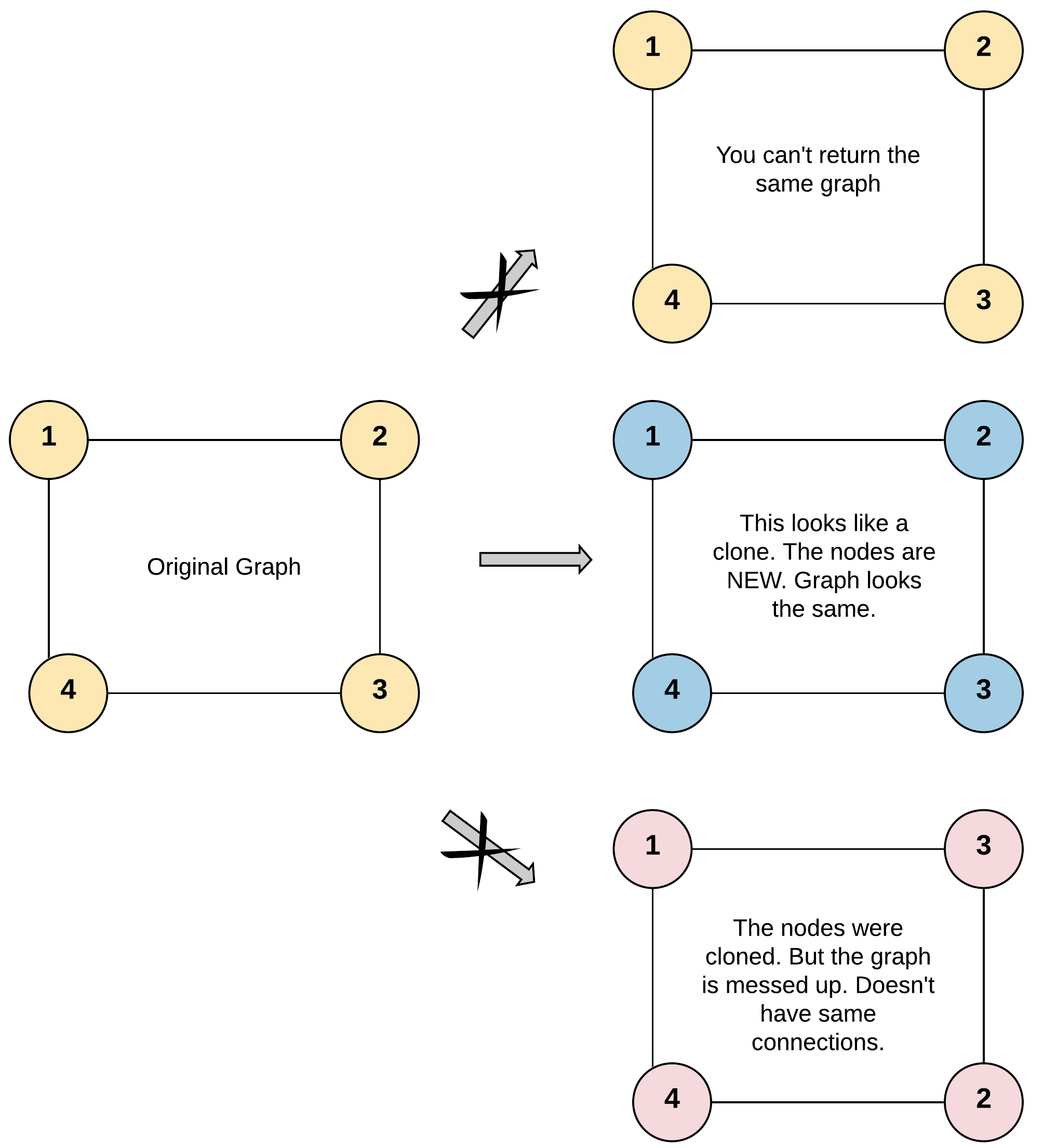
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

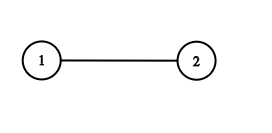
输入：adjList = [[2],[1]]
输出：[[2],[1]]

解题思路

所谓深拷贝，就是构建一张与原图结构、值均一样的图，但是所用的节点不再是原图节点的引用，即每个节点都要新建。

可以用深度优先搜索或者广度优先搜索来做。

思路 1：深度优先搜索

使用哈希表 $visitedDict$ 来存储原图中被访问过的节点和克隆图中对应节点，键值对为「原图被访问过的节点：克隆图中对应节点」。
从给定节点开始，以深度优先搜索的方式遍历原图。
1. 如果当前节点被访问过，则返回隆图中对应节点。
2. 如果当前节点没有被访问过，则创建一个新的节点，并保存在哈希表中。
3. 遍历当前节点的邻接节点列表，递归调用当前节点的邻接节点，并将其放入克隆图中对应节点。
递归结束，返回克隆节点。

思路 1：代码

class Solution:
    def cloneGraph(self, node: 'Node') -> 'Node':
        if not node:
            return node
        visited = dict()

        def dfs(node: 'Node') -> 'Node':
            if node in visited:
                return visited[node]

            clone_node = Node(node.val, [])
            visited[node] = clone_node
            for neighbor in node.neighbors:
                clone_node.neighbors.append(dfs(neighbor))
            return clone_node

        return dfs(node)

思路 1：复杂度分析

时间复杂度： $O(n)$ 。其中 $n$ 为图中节点数量。
空间复杂度： $O(n)$ 。

思路 2：广度优先搜索

使用哈希表 $visited$ 来存储原图中被访问过的节点和克隆图中对应节点，键值对为「原图被访问过的节点：克隆图中对应节点」。使用队列 $queue$ 存放节点。
根据起始节点 $node$ ，创建一个新的节点，并将其添加到哈希表 $visited$ 中，即 visited[node] = Node(node.val, [])。然后将起始节点放入队列中，即 queue.append(node)。
从队列中取出第一个节点 $node\underline{\hspace{0.5em}}u$ 。访问节点 $node\underline{\hspace{0.5em}}u$ 。
遍历节点 $node\underline{\hspace{0.5em}}u$ 的所有未访问邻接节点 $node\underline{\hspace{0.5em}}v$ （节点 $node\underline{\hspace{0.5em}}v$ 不在 $visited$ 中）。
根据节点 $node\underline{\hspace{0.5em}}v$ 创建一个新的节点，并将其添加到哈希表 $visited$ 中，即 visited[node_v] = Node(node_v.val, [])。
然后将节点 $node\underline{\hspace{0.5em}}v$ 放入队列 $queue$ 中，即 queue.append(node_v)。
重复步骤 $3 \sim 6$ ，直到队列 $queue$ 为空。
广度优先搜索结束，返回起始节点的克隆节点（即 $visited[node]$ ）。

思路 2：代码

class Solution:
    def cloneGraph(self, node: 'Node') -> 'Node':
        if not node:
            return node
        
        visited = dict()
        queue = collections.deque()

        visited[node] = Node(node.val, [])
        queue.append(node)

        while queue:
            node_u = queue.popleft()
            for node_v in node_u.neighbors:
                if node_v not in visited:
                    visited[node_v] = Node(node_v.val, [])
                    queue.append(node_v)
                visited[node_u].neighbors.append(visited[node_v])
        
        return visited[node]

思路 2：复杂度分析

时间复杂度： $O(n)$ 。其中 $n$ 为图中节点数量。
空间复杂度： $O(n)$ 。