0240. 搜索二维矩阵 II

ITCharge大约 2 分钟

0240. 搜索二维矩阵 II

标签：二分查找、分治算法
难度：中等

题目链接

0240. 搜索二维矩阵 II - 力扣

题目大意

描述：给定一个 $m \times n$ 大小的有序整数矩阵 $matrix$ 。 $matrix$ 中的每行元素从左到右升序排列，每列元素从上到下升序排列。再给定一个目标值 $target$ 。

要求：判断矩阵中是否可以找到 $target$ ，如果可以找到 $target$ ，返回 True，否则返回 False。

说明：

$m == matrix.length$ 。
$n == matrix[i].length$ 。
$1 \le n, m \le 300$ 。
$-10^9 \le matrix[i][j] \le 10^9$ 。
每行的所有元素从左到右升序排列。
每列的所有元素从上到下升序排列。
$-10^9 \le target \le 10^9$ 。

示例：

示例 1：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：True

示例 2：

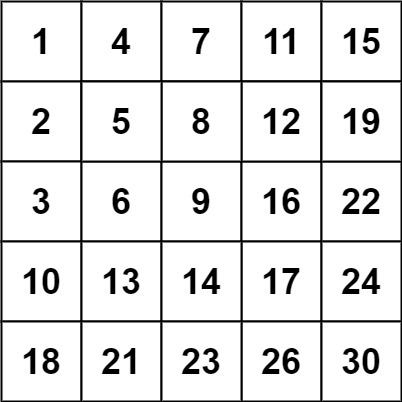
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：False

解题思路

思路 1：二分查找

矩阵是有序的，可以考虑使用二分查找来做。

迭代对角线元素，假设对角线元素的坐标为 $(row, col)$ 。把数组元素按对角线分为右上角部分和左下角部分。
对于当前对角线元素右侧第 $row$ $ro w$ 行、对角线元素下侧第 $col$ $co l$ 列分别进行二分查找。
1. 如果找到目标，直接返回 True。
2. 如果找不到目标，则缩小范围，继续查找。
3. 直到所有对角线元素都遍历完，依旧没找到，则返回 False。

思路 1：代码

class Solution:
    def diagonalBinarySearch(self, matrix, diagonal, target):
        left = 0
        right = diagonal
        while left < right:
            mid = left + (right - left) // 2
            if matrix[mid][mid] < target:
                left = mid + 1
            else:
                right = mid
        return left

    def rowBinarySearch(self, matrix, begin, cols, target):
        left = begin
        right = cols
        while left < right:
            mid = left + (right - left) // 2
            if matrix[begin][mid] < target:
                left = mid + 1
            elif matrix[begin][mid] > target:
                right = mid - 1
            else:
                left = mid
                break
        return begin <= left <= cols and matrix[begin][left] == target

    def colBinarySearch(self, matrix, begin, rows, target):
        left = begin + 1
        right = rows
        while left < right:
            mid = left + (right - left) // 2
            if matrix[mid][begin] < target:
                left = mid + 1
            elif matrix[mid][begin] > target:
                right = mid - 1
            else:
                left = mid
                break
        return begin <= left <= rows and matrix[left][begin] == target

    def searchMatrix(self, matrix, target: int) -> bool:
        rows = len(matrix)
        if rows == 0:
            return False
        cols = len(matrix[0])
        if cols == 0:
            return False

        min_val = min(rows, cols)
        index = self.diagonalBinarySearch(matrix, min_val - 1, target)
        if matrix[index][index] == target:
            return True
        for i in range(index + 1):
            row_search = self.rowBinarySearch(matrix, i, cols - 1, target)
            col_search = self.colBinarySearch(matrix, i, rows - 1, target)
            if row_search or col_search:
                return True
        return False

思路 1：复杂度分析

时间复杂度： $O(min(m, n) \times (\log_2 m + \log_2 n))$ ，其中 $m$ 是矩阵的行数， $n$ 是矩阵的列数。
空间复杂度： $O(1)$ 。