0218. 天际线问题
大约 3 分钟
0218. 天际线问题
- 标签:树状数组、线段树、数组、分治、有序集合、扫描线、堆(优先队列)
- 难度:困难
题目链接
题目大意
城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。
给定所有建筑物的位置和高度所组成的数组 buildings。其中三元素 buildings[i] = [left_i, right_i, height_i] 表示 left_i 是第 i 座建筑物左边界的 x 坐标。right_i 是第 i 座建筑物右边界的 x 坐标,height_i 是第 i 做建筑物的高度。
要求:返回由这些建筑物形成的天际线 。
- 天际线:由 “关键点” 组成的列表,格式
[[x1, y1], [x2, y2], [x3, y3], ...],并按x坐标进行排序。 - 关键点:水平线段的左端点。列表中最后一个点是最右侧建筑物的终点,
y坐标始终为0,仅用于标记天际线的终点。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
注意:输出天际线中不得有连续的相同高度的水平线。
- 例如
[..., [2 3], [4 5], [7 5], [11 5], [12 7], ...]是不正确的答案;三条高度为5的线应该在最终输出中合并为一个:[..., [2 3], [4 5], [12 7], ...]。
示例:
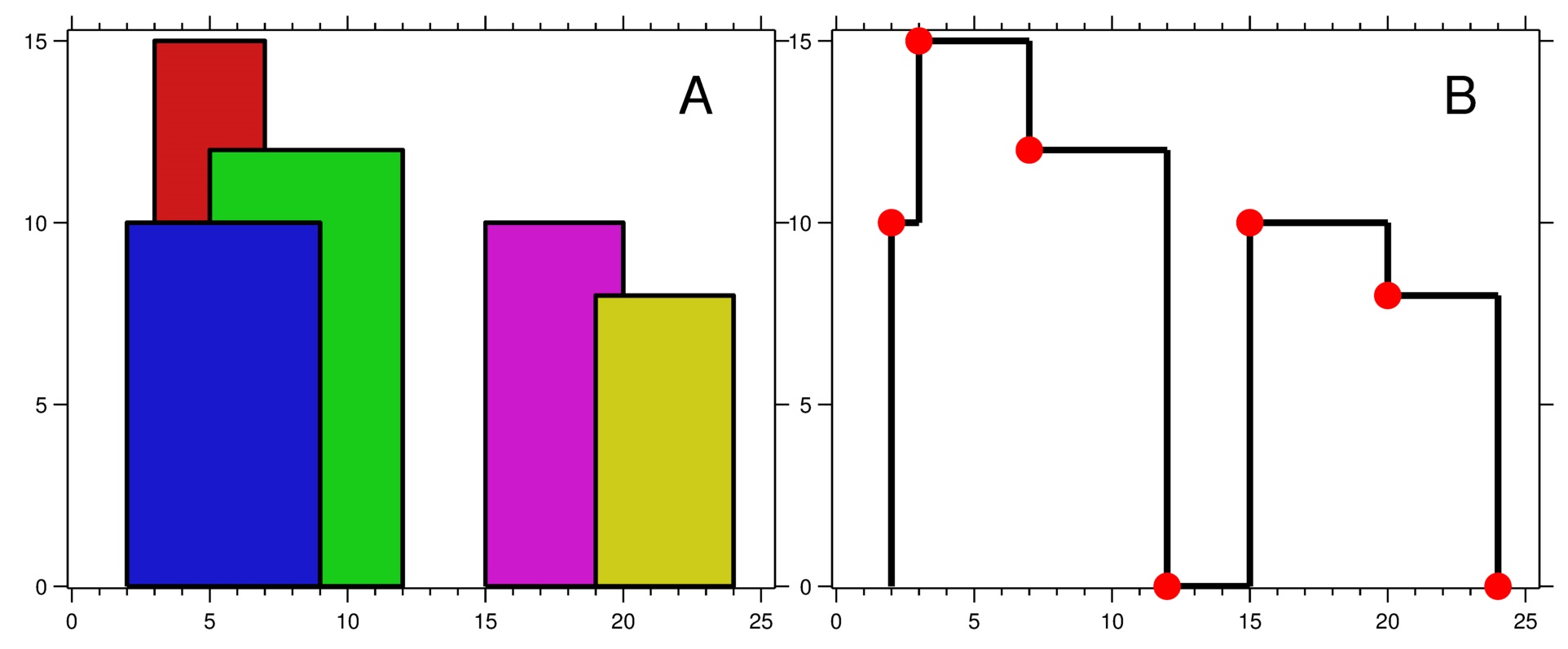
- 图 A 显示输入的所有建筑物的位置和高度。
- 图 B 显示由这些建筑物形成的天际线。图 B 中的红点表示输出列表中的关键点。
解题思路
可以看出来:关键点的横坐标都在建筑物的左右边界上。
我们可以将左右边界最高处的坐标存入 points 数组中,然后按照建筑物左边界、右边界的高度进行排序。
然后用一条条「垂直于 x 轴的扫描线」,从所有建筑物的最左侧依次扫描到最右侧。从而将建筑物分割成规则的矩形。
不难看出:相邻的两个坐标的横坐标与矩形所能达到的最大高度构成了一个矩形。相邻两个坐标的横坐标可以从排序过的 points 数组中依次获取,矩形所能达到的最大高度可以用一个优先队列(堆)max_heap 来维护。使用数组 ans 来作为答案答案。
在依次从左到右扫描坐标时:
- 当扫描到建筑物的左边界时,说明必然存在一条向右延伸的边。此时将高度加入到优先队列中。
- 当扫描到建筑物的右边界时,说明从之前的左边界延伸的边结束了,此时将高度从优先队列中移除。
因为三条高度相同的线应该合并为一个,所以我们用 prev 来记录之前上一个矩形高度。
- 如果当前矩形高度
curr与之前矩形高度prev相同,则跳过。 - 如果当前矩形高度
curr与之前矩形高度prev不相同,则将其加入到答案数组中,并更新上一矩形高度prev的值。
最后,输出答案 ans。
代码
from sortedcontainers import SortedList
class Solution:
def getSkyline(self, buildings: List[List[int]]) -> List[List[int]]:
ans = []
points = []
for building in buildings:
left, right, hight = building[0], building[1], building[2]
points.append([left, -hight])
points.append([right, hight])
points.sort(key=lambda x:(x[0], x[1]))
prev = 0
max_heap = SortedList([prev])
for point in points:
x, height = point[0], point[1]
if height < 0:
max_heap.add(-height)
else:
max_heap.remove(height)
curr = max_heap[-1]
if curr != prev:
ans.append([x, curr])
prev = curr
return ans