0351. 安卓系统手势解锁
大约 4 分钟
0351. 安卓系统手势解锁
- 标签:动态规划、回溯
- 难度:中等
题目链接
题目大意
描述:安卓系统手势解锁的界面是一个编号为 、大小为 的网格。用户可以设定一个「解锁模式」,按照一定顺序经过 个点,构成一个「解锁手势」。现在给定两个整数,分别为 和 。
要求:计算出有多少种不同且有效的解锁模式数量,其中每种解锁模式至少需要经过 个点,但是不超过 个点。
说明:
有效的解锁模式:
- 解锁模式中所有点不能重复。
- 如果解锁模式中两个点是按顺序经过的,那么这两个点之间的手势轨迹不能跨过其他任何未被经过的点。
一些有效和无效解锁模式示例:
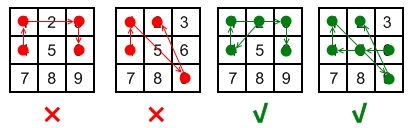
- 无效手势:,连接点 和点 时经过了未被连接过的 号点。
- 无效手势:,连接点 和点 时经过了未被连接过的 号点。
- 有效手势:,连接点 和点 是有效的,因为虽然它经过了点 ,但是点 在该手势中之前已经被连过了。
- 有效手势:,连接点 和点 是有效的,因为虽然它经过了按键 ,但是点 在该手势中之前已经被连过了。
。
如果经过的点不同或者经过点的顺序不同,表示为不同的解锁模式。
示例:
- 示例 1:
输入:m = 1, n = 1
输出:9
- 示例 2:
输入:m = 1, n = 2
输出:65
解题思路
思路 1:状态压缩 + 记忆化搜索
因为手势解锁的界面是一个编号为 、大小为 的网格,所以我们可以用一个 位长度的二进制数 来表示当前解锁模式中按键的选取情况。
因为解锁模式中两个点之间的手势轨迹不能跨过其他任何未被经过的点,所以我们可以预先使用一个哈希表 将手势轨迹跨过其他点的情况存储下来,便于判断当前手势轨迹是否有效。
接下来我们使用深度优先搜索方法,将所有有效的解锁模式统计出来,具体做法如下:
- 定义一个全局变量 用于统计所有有效的解锁模式的方案数。
- 定义一个深度优先搜索方法为
def dfs(state, cur, step):,表示当前键位选择情况为 ,从当前键位 出发,已经走了 的有效解锁模式。- 当 在区间 中时,统计有效解锁模式方案数,即:令 加 。
- 当 到达步数上限 时,直接返回。
- 遍历下一步(第 步)可选择的键位 ,判断键位 是否有效。
- 如果到达 没有跨过其他键( 不在 中),或者到达 跨过的键位是已经经过的键 (),则继续调用
dfs(state | (1 << k), k, step + 1),其中stete | (1 << k)表示下一步选择 的状态。
- 遍历开始位置 ,从 1 ~ 9 每个数字开始出发,调用
dfs(1 << i, i, 1),进行所有有效的解锁模式的统计。 - 最后输出 。
思路 1:代码
class Solution:
def numberOfPatterns(self, m: int, n: int) -> int:
# 将手势轨迹跨过点的情况存入哈希表中
graph = {
1: {3: 2, 7: 4, 9: 5},
2: {8: 5},
3: {1: 2, 7: 5, 9: 6},
4: {6: 5},
5: {},
6: {4: 5},
7: {1: 4, 3: 5, 9: 8},
8: {2: 5},
9: {1: 5, 3: 6, 7: 8},
}
ans = 0
def dfs(state, cur, step):
nonlocal ans
if m <= step <= n:
ans += 1
if step == n:
return
for k in range(1, 10):
if state >> k & 1 != 0:
continue
if k not in graph[cur] or state >> graph[cur][k] & 1:
dfs(state | (1 << k), k, step + 1)
for i in range(1, 10):
dfs(1 << i, i, 1) # 从 1 ~ 9 每个数字开始出发
return ans
思路 1:复杂度分析
- 时间复杂度:。
- 空间复杂度:。