0310. 最小高度树

ITCharge大约 6 分钟

0310. 最小高度树

标签：深度优先搜索、广度优先搜索、图、拓扑排序
难度：中等

题目链接

0310. 最小高度树 - 力扣

题目大意

描述：有一棵包含 $n$ 个节点的树，节点编号为 $0 \sim n - 1$ 。给定一个数字 $n$ 和一个有 $n - 1$ 条无向边的 $edges$ 列表来表示这棵树。其中 $edges[i] = [ai, bi]$ 表示树中节点 $ai$ 和 $bi$ 之间存在一条无向边。

可以选择树中的任何一个节点作为根，当选择节点 $x$ 作为根节点时，设结果树的高度为 $h$ 。在所有可能的树种，具有最小高度的树（即 $min(h)$ ）被成为最小高度树。

要求：找到所有的最小高度树并按照任意顺序返回他们的根节点编号列表。

说明：

树的高度：指根节点和叶子节点之间最长向下路径上边的数量。
$1 \le n \le 2 * 10^4$ 。
$edges.length == n - 1$ 。
$0 \le ai, bi < n$ 。
$ai \ne bi$ 。
所有 $(ai, bi)$ 互不相同。
给定的输入保证是一棵树，并且不会有重复的边。

示例：

示例 1：

输入：n = 4, edges = [[1,0],[1,2],[1,3]]
输出：[1]
解释：如图所示，当根是标签为 1 的节点时，树的高度是 1 ，这是唯一的最小高度树。

示例 2：

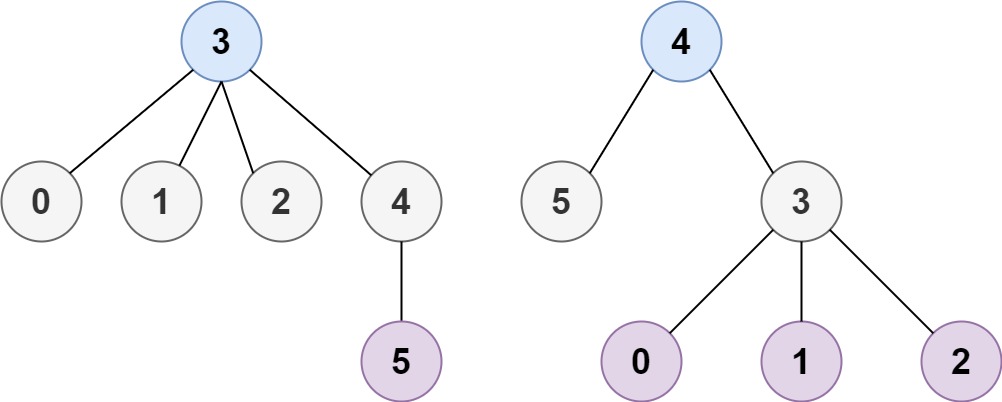
输入：n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
输出：[3,4]

解题思路

思路 1：树形 DP + 二次遍历换根法

最容易想到的做法是：枚举 $n$ 个节点，以每个节点为根节点，然后进行深度优先搜索，求出每棵树的高度。最后求出所有树中的最小高度即为答案。但这种做法的时间复杂度为 $O(n^2)$ ，而 $n$ 的范围为 $[1, 2 * 10^4]$ ，这样做会导致超时，因此需要进行优化。

在上面的算法中，在一轮深度优先搜索中，除了可以得到整棵树的高度之外，在搜索过程中，其实还能得到以每个子节点为根节点的树的高度。如果我们能够利用这些子树的高度信息，快速得到以其他节点为根节点的树的高度，那么我们就能改进算法，以更小的时间复杂度解决这道题。这就是二次遍历与换根法的思想。

第一次遍历：自底向上的计算出每个节点 $u$ 向下走（即由父节点 $u$ 向子节点 $v$ 走）的最长路径 $down1[u]$ 、次长路径 $down2[i]$ ，并记录向下走最长路径所经过的子节点 $p[u]$ ，方便第二次遍历时计算。
第二次遍历：自顶向下的计算出每个节点 $v$ $v$ 向上走（即由子节点 $v$ $v$ 向父节点 $u$ $u$ 走）的最长路径 $up[v]$ $u p [v]$ 。需要注意判断 $u$ $u$ 向下走的最长路径是否经过了节点 $v$ $v$ 。
1. 如果经过了节点 $v$ ，则向上走的最长路径，取决于「父节点 $u$ 向上走的最长路径」与「父节点 $u$ 向下走的次长路径」的较大值，再加上 $1$ 。
2. 如果没有经过节点 $v$ ，则向上走的最长路径，取决于「父节点 $u$ 向上走的最长路径」与「父节点 $u$ 向下走的最长路径」的较大值，再加上 $1$ 。
接下来，我们通过枚举 $n$ 个节点向上走的最长路径与向下走的最长路径，从而找出所有树中的最小高度，并将所有最小高度树的根节点放入答案数组中并返回。

整个算法具体步骤如下：

使用邻接表的形式存储树。
定义第一个递归函数 dfs(u, fa) 用于计算每个节点向下走的最长路径 $down1[u]$ $d o w n 1 [u]$ 、次长路径 $down2[u]$ $d o w n 2 [u]$ ，并记录向下走的最长路径所经过的子节点 $p[u]$ $p [u]$ 。
1. 对当前节点的相邻节点进行遍历。
2. 如果相邻节点是父节点，则跳过。
3. 递归调用 dfs(v, u) 函数计算邻居节点的信息。
4. 根据邻居节点的信息计算当前节点的高度，并更新当前节点向下走的最长路径 $down1[u]$ 、当前节点向下走的次长路径 $down2$ 、取得最长路径的子节点 $p[u]$ 。
定义第二个递归函数 reroot(u, fa) 用于计算每个节点作为新的根节点时向上走的最长路径 $up[v]$ $u p [v]$ 。
1. 对当前节点的相邻节点进行遍历。
2. 如果相邻节点是父节点，则跳过。
3. 根据当前节点 $u$ $u$ 的高度和相邻节点 $v$ $v$ 的信息更新 $up[v]$ $u p [v]$ 。同时需要判断节点 $u$ $u$ 向下走的最长路径是否经过了节点 $v$ $v$ 。
  1. 如果经过了节点 $v$ ，则向上走的最长路径，取决于「父节点 $u$ 向上走的最长路径」与「父节点 $u$ 向下走的次长路径」的较大值，再加上 $1$ ，即： $up[v] = max(up[u], down2[u]) + 1$ 。
  2. 如果没有经过节点 $v$ ，则向上走的最长路径，取决于「父节点 $u$ 向上走的最长路径」与「父节点 $u$ 向下走的最长路径」的较大值，再加上 $1$ ，即： $up[v] = max(up[u], down1[u]) + 1$ 。
4. 递归调用 reroot(v, u) 函数计算邻居节点的信息。
调用 dfs(0, -1) 函数计算每个节点的最长路径。
调用 reroot(0, -1) 函数计算每个节点作为新的根节点时的最长路径。
找到所有树中的最小高度。
将所有最小高度的节点放入答案数组中并返回。

思路 1：代码

class Solution:
    def findMinHeightTrees(self, n: int, edges: List[List[int]]) -> List[int]:
        graph = [[] for _ in range(n)]
        for u, v in edges:
            graph[u].append(v)
            graph[v].append(u)
		
        # down1 用于记录向下走的最长路径 
        down1 = [0 for _ in range(n)]
        # down2 用于记录向下走的最长路径
        down2 = [0 for _ in range(n)]
        p = [0 for _ in range(n)]
        # 自底向上记录最长路径、次长路径
        def dfs(u, fa):
            for v in graph[u]:
                if v == fa:
                    continue
                # 自底向上统计信息
                dfs(v, u)                   
                height = down1[v] + 1
                if height >= down1[u]:
                    down2[u] = down1[u]
                    down1[u] = height
                    p[u] = v
                elif height > down2[u]:
                    down2[u] = height

        # 进行换根动态规划，自顶向下统计向上走的最长路径
        up = [0 for _ in range(n)]
        def reroot(u, fa):
            for v in graph[u]:
                if v == fa:
                    continue
                if p[u] == v:
                    up[v] = max(up[u], down2[u]) + 1
                else:
                    up[v] = max(up[u], down1[u]) + 1
                # 自顶向下统计信息
                reroot(v, u)                            

        dfs(0, -1)
        reroot(0, -1)

        # 找到所有树中的最小高度
        min_h = 1e9
        for i in range(n):
            min_h = min(min_h, max(down1[i], up[i]))

        # 将所有最小高度的节点放入答案数组中并返回
        res = []
        for i in range(n):
            if max(down1[i], up[i]) == min_h:
                res.append(i)

        return res

思路 1：复杂度分析

时间复杂度： $O(n)$ 。
空间复杂度： $O(n)$ 。