0391. 完美矩形

• 标签：数组、扫描线
• 难度：困难

题目链接

• 0391. 完美矩形 - 力扣

题目大意

描述：给定一个数组 rectangles，其中 rectangles[i] = [xi, yi, ai, bi] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi)，右上顶点是 (ai, bi)。

要求：如果所有矩形一起精确覆盖了某个矩形区域，则返回 True；否则，返回 False。

说明：

• $1 \le rectangles.length \le 2 * 10^4$。
• $rectangles[i].length == 4$。
• $-10^5 \le xi, yi, ai, bi \le 10^5$。

示例：

• 示例 1：

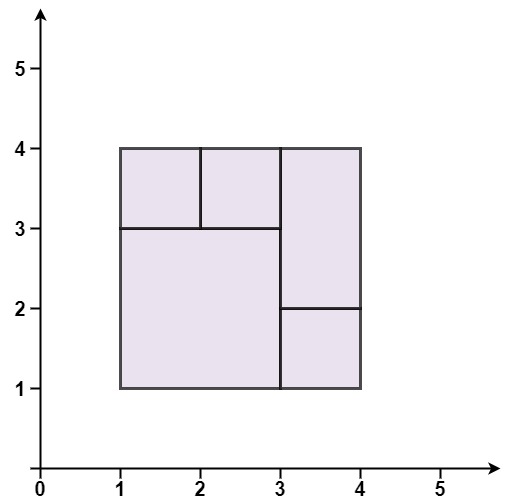
输入：rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出：True
解释：5 个矩形一起可以精确地覆盖一个矩形区域。 

• 示例 2：

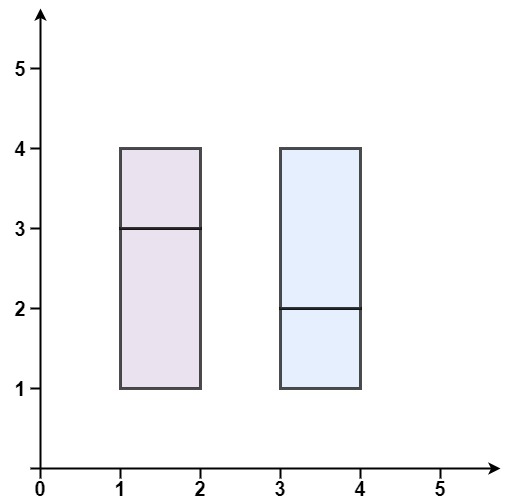
输入：rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出：false
解释：两个矩形之间有间隔，无法覆盖成一个矩形。

• 示例 3：

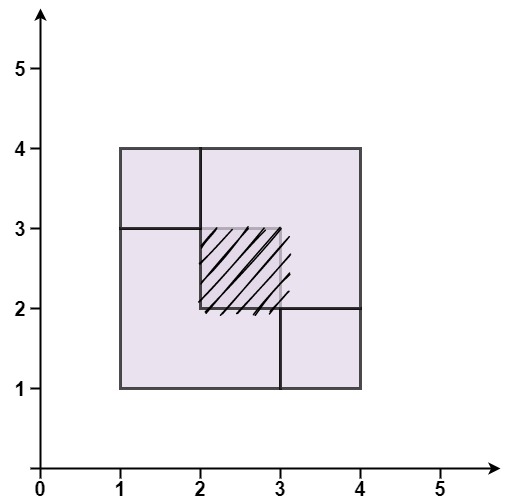
输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
输出：False
解释：因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

解题思路

思路 1：线段树

首先我们要先判断所有小矩形的面积和是否等于外接矩形区域的面积。如果不相等，则说明出现了重叠或者空缺，明显不符合题意。

在两者面积相等的情况下，还可能会发生重叠的情况。接下来我们要思考如何判断重叠。

• 第一种思路：暴力枚举所有矩形对，两两进行比较，判断是否出现了重叠。这样的时间复杂度是 $O(n^2)$，容易超时。
• 第二种思路：
  • 如果所有小矩形可以精确覆盖某个矩形区域，那这些小矩形一定是相互挨着的，也就是说相邻两个矩形的边会重合在一起。比如说 矩形 A 下边刚好是 B 的上边，或者是 B 的上边的一部分。
  • 我们可以固定一个坐标轴，比如说固定 y 轴，然后只看水平方向上所有矩形的边。然后我们就会发现，满足题意要求的矩形区域中，纵坐标为 y 的平行线上，「所有上边纵坐标为 y 的矩形上边区间」与「所有下边纵坐标为 y 的矩形下边区间」是完全一样，或者说重合在一起的（除了矩形矩形最上边和最下边只有一条，不会重合之外）。
  • 这样我们就可以用扫描线的思路，建立一个线段树。然后先固定纵坐标 y，将「所有上边纵坐标为 y 的矩形上边区间」对应的区间值减 1，再将「所有下边纵坐标为 y 的矩形下边区间」对应的区间值加 1。然后查询整个线代树区间值，如果区间值超过 1，则说明发生了重叠，不符合题目要求。如果扫描完所有的纵坐标，没有发生重叠，则说明符合题意要求。
  • 因为横坐标的范围为 $[-10^5,10^5]$，但是最多只有 $2 * 10^4$ 个横坐标，所以我们可以先对所有坐标做一下离散化处理，再根据离散化之后的横坐标建立线段树。

具体步骤如下：

1. 通过遍历所有小矩形，计算出所有小矩形的面积和为 area。同时计算出矩形区域四个顶点位置，并根据四个顶点计算出矩形区域的面积为 total_area。如果所有小矩形面积不等于矩形区域的面积，则直接返回 False。
2. 再次遍历所有小矩形，将所有坐标点进行离散化处理，将其编号存入两个哈希表 x_dict、y_dict。
3. 使用哈希表 top_dict、bottom_dict 分别存储每个矩阵的上下两条边。将上下两条边的横坐标 x1、x2。分别存入到 top_dict[y_dict[y2]]、top_dict[y_dict[y2]] 中。
4. 建立区间长度为横坐标个数的线段树 STree。
5. 遍历所有的纵坐标，对于纵坐标 i：
   1. 先遍历当前纵坐标下矩阵的上边数组，即 top_dict[i]，取出边的横坐标 x1、x2。令区间 [x1, x2 - 1] 上的值减 1。
   2. 再遍历当前纵坐标下矩阵的下边数组，即 bottom_dict[i]，取出边的横坐标 x1、x2。令区间 [x1, x2 - 1] 上的值加 1。
   3. 如果上下边覆盖完之后，被覆盖次数超过了 1，则说明出现了重叠，直接返回 Fasle。
6. 如果遍历完所有的纵坐标，没有发现重叠，则返回 True。

思路 1：线段树代码

# 线段树的节点类
class SegTreeNode:
    def __init__(self, val=0):
        self.left = -1                              # 区间左边界
        self.right = -1                             # 区间右边界
        self.val = val                              # 节点值（区间值）
        self.lazy_tag = None                        # 区间和问题的延迟更新标记
        
        
# 线段树类
class SegmentTree:
    # 初始化线段树接口
    def __init__(self, nums, function):
        self.size = len(nums)
        self.tree = [SegTreeNode() for _ in range(4 * self.size)]  # 维护 SegTreeNode 数组
        self.nums = nums                            # 原始数据
        self.function = function                    # function 是一个函数，左右区间的聚合方法
        if self.size > 0:
            self.__build(0, 0, self.size - 1)
            
    # 单点更新接口：将 nums[i] 更改为 val
    def update_point(self, i, val):
        self.nums[i] = val
        self.__update_point(i, val, 0)
        
    # 区间更新接口：将区间为 [q_left, q_right] 上的所有元素值加上 val
    def update_interval(self, q_left, q_right, val):
        self.__update_interval(q_left, q_right, val, 0)
        
    # 区间查询接口：查询区间为 [q_left, q_right] 的区间值
    def query_interval(self, q_left, q_right):
        return self.__query_interval(q_left, q_right, 0)
    
    # 获取 nums 数组接口：返回 nums 数组
    def get_nums(self):
        for i in range(self.size):
            self.nums[i] = self.query_interval(i, i)
        return self.nums
    
    
    # 以下为内部实现方法
    
    # 构建线段树实现方法：节点的存储下标为 index，节点的区间为 [left, right]
    def __build(self, index, left, right):
        self.tree[index].left = left
        self.tree[index].right = right
        if left == right:                           # 叶子节点，节点值为对应位置的元素值
            self.tree[index].val = self.nums[left]
            return
    
        mid = left + (right - left) // 2            # 左右节点划分点
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        self.__build(left_index, left, mid)         # 递归创建左子树
        self.__build(right_index, mid + 1, right)   # 递归创建右子树
        self.__pushup(index)                        # 向上更新节点的区间值
    
    # 区间更新实现方法
    def __update_interval(self, q_left, q_right, val, index):
        left = self.tree[index].left
        right = self.tree[index].right
        
        if left >= q_left and right <= q_right:     # 节点所在区间被 [q_left, q_right] 所覆盖        
            if self.tree[index].lazy_tag is not None:
                self.tree[index].lazy_tag += val    # 将当前节点的延迟标记增加 val
            else:
                self.tree[index].lazy_tag = val     # 将当前节点的延迟标记增加 val
            self.tree[index].val += val             # 当前节点所在区间每个元素值增加 val
            return
    
        if right < q_left or left > q_right:        # 节点所在区间与 [q_left, q_right] 无关
            return
    
        self.__pushdown(index)                      # 向下更新节点的区间值
    
        mid = left + (right - left) // 2            # 左右节点划分点
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        if q_left <= mid:                           # 在左子树中更新区间值
            self.__update_interval(q_left, q_right, val, left_index)
        if q_right > mid:                           # 在右子树中更新区间值
            self.__update_interval(q_left, q_right, val, right_index)
    
        self.__pushup(index)                        # 向上更新节点的区间值
    
    # 区间查询实现方法：在线段树中搜索区间为 [q_left, q_right] 的区间值
    def __query_interval(self, q_left, q_right, index):
        left = self.tree[index].left
        right = self.tree[index].right
        
        if left >= q_left and right <= q_right:     # 节点所在区间被 [q_left, q_right] 所覆盖
            return self.tree[index].val             # 直接返回节点值
        if right < q_left or left > q_right:        # 节点所在区间与 [q_left, q_right] 无关
            return 0
    
        self.__pushdown(index)
    
        mid = left + (right - left) // 2            # 左右节点划分点
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        res_left = 0                                # 左子树查询结果
        res_right = 0                               # 右子树查询结果
        if q_left <= mid:                           # 在左子树中查询
            res_left = self.__query_interval(q_left, q_right, left_index)
        if q_right > mid:                           # 在右子树中查询
            res_right = self.__query_interval(q_left, q_right, right_index)
    
        return self.function(res_left, res_right)   # 返回左右子树元素值的聚合计算结果
    
    # 向上更新实现方法：更新下标为 index 的节点区间值 等于 该节点左右子节点元素值的聚合计算结果
    def __pushup(self, index):
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        self.tree[index].val = self.function(self.tree[left_index].val, self.tree[right_index].val)
        
    # 向下更新实现方法：更新下标为 index 的节点所在区间的左右子节点的值和懒惰标记
    def __pushdown(self, index):
        lazy_tag = self.tree[index].lazy_tag
        if lazy_tag is None: 
            return
        
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        
        if self.tree[left_index].lazy_tag is not None:
            self.tree[left_index].lazy_tag += lazy_tag  # 更新左子节点懒惰标记
        else:
            self.tree[left_index].lazy_tag = lazy_tag
        self.tree[left_index].val += lazy_tag
        
        if self.tree[right_index].lazy_tag is not None:
            self.tree[right_index].lazy_tag += lazy_tag # 更新右子节点懒惰标记
        else:
            self.tree[right_index].lazy_tag = lazy_tag
        self.tree[right_index].val += lazy_tag 
        self.tree[index].lazy_tag = None            # 更新当前节点的懒惰标记
        
        
class Solution:
    def isRectangleCover(self, rectangles) -> bool:
        left, right, bottom, top  = math.inf, -math.inf, math.inf, -math.inf
        area = 0
        x_set, y_set = set(), set()
        
        for rectangle in rectangles:
            x1, y1, x2, y2 = rectangle
            left, right = min(left, x1), max(right, x2)
            bottom, top  = min(bottom, y1), max(top, y2)
            area += (y2 - y1) * (x2 - x1)
            x_set.add(x1)
            x_set.add(x2)
            y_set.add(y1)
            y_set.add(y2)
            
        total_area = (top - bottom) * (right - left)
        
        # 判断所有小矩形面积是否等于所有矩形顶点构成最大矩形面积，不等于则直接返回 False
        if area != total_area:
            return False
        
        # 离散化处理所有点的横坐标、纵坐标
        x_dict, y_dict = dict(), dict()
        
        idx = 0
        for x in sorted(list(x_set)):
            x_dict[x] = idx
            idx += 1
            
        idy = 0
        for y in sorted(list(y_set)):
            y_dict[y] = idy
            idy += 1
            
        # 使用哈希表 top_dict、bottom_dict 分别存储每个矩阵的上下两条边。
        bottom_dict, top_dict = collections.defaultdict(list), collections.defaultdict(list)
        for i in range(len(rectangles)):
            x1, y1, x2, y2 = rectangles[i] 
            bottom_dict[y_dict[y1]].append([x_dict[x1], x_dict[x2]])
            top_dict[y_dict[y2]].append([x_dict[x1], x_dict[x2]])
            
        # 建立线段树
        self.STree = SegmentTree([0 for _ in range(len(x_set))], lambda x, y: max(x, y))
        
        for i in range(idy):
            for x1, x2 in top_dict[i]:
                self.STree.update_interval(x1, x2 - 1, -1)
            for x1, x2 in bottom_dict[i]:
                self.STree.update_interval(x1, x2 - 1, 1)
            cnt = self.STree.query_interval(0, len(x_set) - 1)
            if cnt  > 1:
                return False
        return True

参考资料

• 【题解】线段树+扫描线 - 完美矩形 - 力扣