0376. 摆动序列

• 标签：贪心、数组、动态规划
• 难度：中等

题目链接

• 0376. 摆动序列 - 力扣

题目大意

如果一个数组序列中，连续项之间的差值是严格的在正数、负数之间交替，则称该数组序列为「摆动序列」。第一个差值可能为正数，也可能为负数。只有一个元素或者还有两个不等元素的数组序列也可以看做是摆动序列。

• 例如：[1, 7, 4, 9, 2, 5] 是摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
• 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列。第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

现在给定一个整数数组 nums，返回 nums 中作为「摆动序列」的「最长子序列长度」。

解题思路

我们先通过一个例子来说明如何求摆动数组最长子序列的长度。

下图是 nums = [1,17,5,10,13,15,10,5,16,8] 的图示。

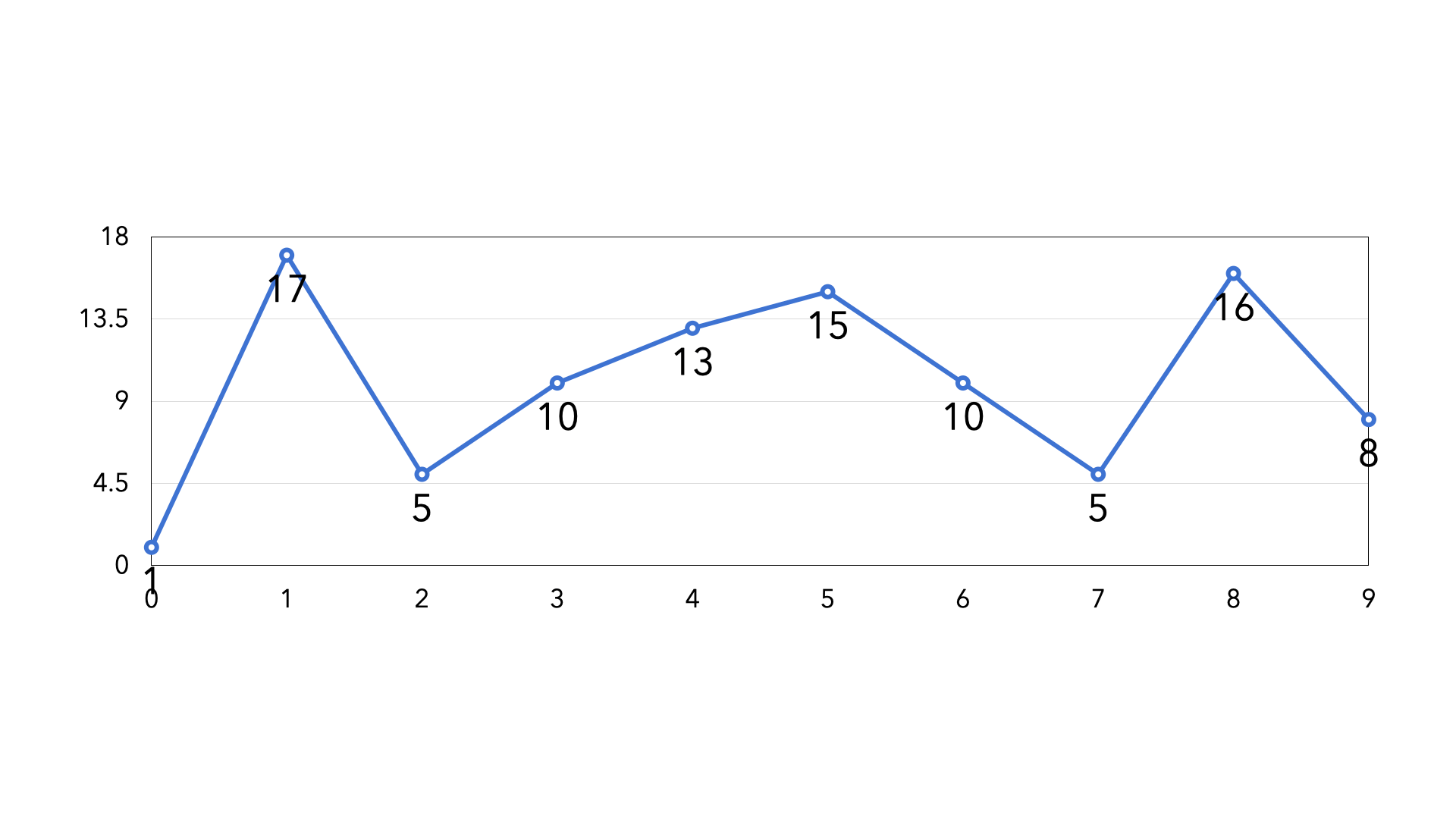
根据题意可知，摆动数组中连续项的差值是正负交替的，直观表现就像是一条高低起伏的山脉，或者像一把锯齿。

观察图像可知，貌似当我们不断交错的选择山脉的「波峰」和「波谷」作为子序列的元素，就会使摆动数组的子序列尽可能的长。例如下图选择 [1, 17, 5, 15, 5, 16, 8]。

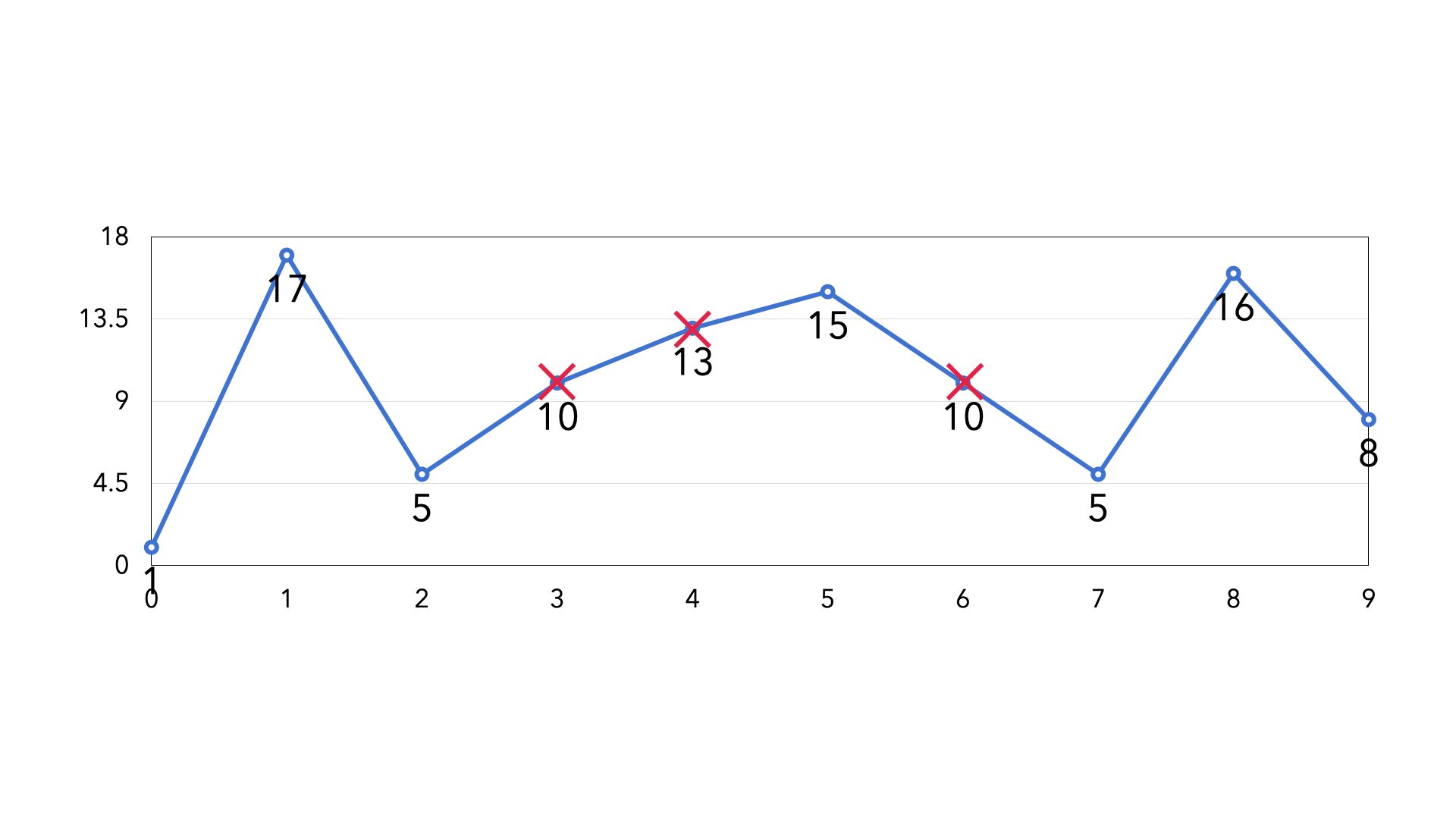
可是为什么选择「峰」「谷」就能使摆动数组的子序列尽可能的长？为什么我们不选择「中间元素」呢？

其实也可以选择「中间元素」，因为一路从波谷爬坡到波峰再到波谷，和从波谷爬坡到半山腰再回到波谷所形成的摆动数组最长子序列的长度是一样的。

只不过如果选择中间元素，这个中间元素两侧必有波峰和波谷，我们假设选择的序列出现顺序为：「谷 -> 中间元素 -> 谷」，则「谷」和「谷」中间的「峰」必定没有出现在选择的序列中，我们必然可以将选择的「中间元素」替换为「峰」。

同理，「峰 -> 中间元素 -> 峰」中选择的「中间元素」必然也可以替换为「谷」。

所以既然中可以替换，所以我们干脆直接选择「峰」「谷」就可以满足最长子序列的长度。

所以题目就变为了：统计序列中「峰」「谷」的数量。

记录下前一对连续项的差值、当前对连续项的差值，并判断是否是互为正负的。

• 如果互为正负，则为「峰」或「谷」，记录下个数，并更新前一对连续项的差值。
• 如果符号相同，则继续向后判断。

代码

class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        size = len(nums)
        cur_diff = 0
        pre_diff = 0
        res = 1
        for i in range(size - 1):
            cur_diff = nums[i + 1] - nums[i]
            if (cur_diff > 0 and pre_diff <= 0) or (pre_diff >= 0 and cur_diff < 0):
                res += 1
                pre_diff = cur_diff
        return res