0417. 太平洋大西洋水流问题

• 标签：深度优先搜索、广度优先搜索、数组、矩阵
• 难度：中等

题目链接

• 0417. 太平洋大西洋水流问题 - 力扣

题目大意

描述：给定一个 m * n 大小的二维非负整数矩阵 heights 来表示一片大陆上各个单元格的高度。heights[i][j] 表示第 i 行第 j 列所代表的陆地高度。这个二维矩阵所代表的陆地被太平洋和大西洋所包围着。左上角是「太平洋」，右下角是「大西洋」。规定水流只能按照上、下、左、右四个方向流动，且只能从高处流到低处，或者在同等高度上流动。

要求：找出代表陆地的二维矩阵中，水流既可以从该处流动到太平洋，又可以流动到大西洋的所有坐标。以二维数组 res 的形式返回，其中 res[i] = [ri, ci] 表示雨水从单元格 (ri, ci) 既可流向太平洋也可流向大西洋。

说明：

• $m == heights.length$。
• $n == heights[r].length$。
• $1 \le m, n \le 200$。
• $0 \le heights[r][c] \le 10^5$。

示例：

• 示例 1：

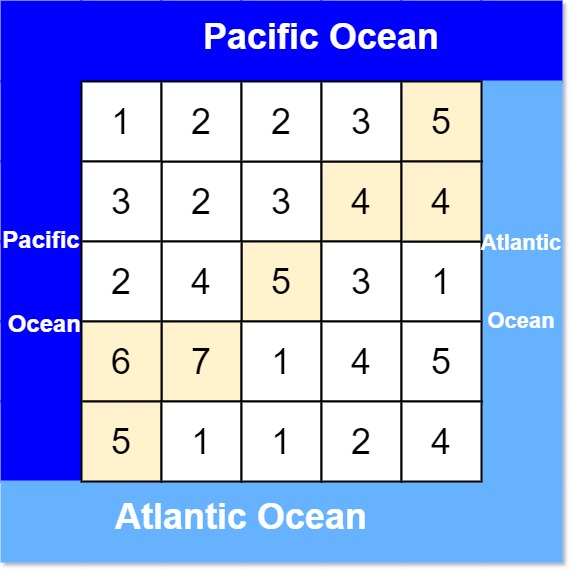
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

• 示例 2：

输入: heights = [[2,1],[1,2]]
输出: [[0,0],[0,1],[1,0],[1,1]]

解题思路

思路 1：深度优先搜索

雨水由高处流向低处，如果我们根据雨水的流向搜索，来判断是否能从某一位置流向太平洋和大西洋不太容易。我们可以换个思路。

1. 分别从太平洋和大西洋（就是矩形边缘）出发，逆流而上，找出水流逆流能达到的地方，可以用两个二维数组 pacific、atlantic 分别记录太平洋和大西洋能到达的位置。
2. 然后再对二维数组进行一次遍历，找出两者交集的位置，就是雨水既可流向太平洋也可流向大西洋的位置，将其加入答案数组 res 中。
3. 最后返回答案数组 res。

思路 1：代码

class Solution:
    def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
        rows, cols = len(heights), len(heights[0])
        pacific = [[False for _ in range(cols)] for _ in range(rows)]
        atlantic = [[False for _ in range(cols)] for _ in range(rows)]

        directs = [(0, 1), (0, -1), (1, 0), (-1, 0)]

        def dfs(i, j, visited):
            visited[i][j] = True
            for direct in directs:
                new_i = i + direct[0]
                new_j = j + direct[1]
                if new_i < 0 or new_i >= rows or new_j < 0 or new_j >= cols:
                    continue
                if heights[new_i][new_j] >= heights[i][j] and not visited[new_i][new_j]:
                    dfs(new_i, new_j, visited)

        for j in range(cols):
            dfs(0, j, pacific)
            dfs(rows - 1, j, atlantic)

        for i in range(rows):
            dfs(i, 0, pacific)
            dfs(i, cols - 1, atlantic)

        res = []
        for i in range(rows):
            for j in range(cols):
                if pacific[i][j] and atlantic[i][j]:
                    res.append([i, j])
        return res

思路 1：复杂度分析

• 时间复杂度：$O(m \times n)$。其中 $m$ 和 $n$ 分别为行数和列数。
• 空间复杂度：$O(m \times n)$。