0542. 01 矩阵

ITCharge大约 3 分钟

0542. 01 矩阵

标签：广度优先搜索、数组、动态规划、矩阵
难度：中等

题目链接

0542. 01 矩阵 - 力扣

题目大意

描述：给定一个 $m * n$ 大小的、由 0 和 1 组成的矩阵 $mat$ 。

要求：输出一个大小相同的矩阵 $res$ ，其中 $res[i][j]$ 表示对应位置元素（即 $mat[i][j]$ ）到最近的 $0$ 的距离。

说明：

两个相邻元素间的距离为 $1$ 。
$m == mat.length$ 。
$n == mat[i].length$ 。
$1 \le m, n \le 10^4$ 。
$1 \le m * n \le 10^4$ 。
$mat[i][j] === 0$ 或者 $mat[i][j] == 1$ 。
$mat$ 中至少有一个 $0$ 。

示例：

示例 1：

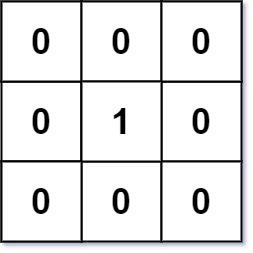
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

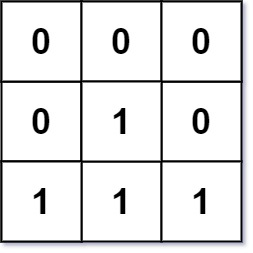
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

解题思路

思路 1：广度优先搜索

题目要求的是每个 1 到 0的最短曼哈顿距离。

比较暴力的做法是，从每个 1 开始进行广度优先搜索，每一步累积距离，当搜索到第一个 0，就是离这个 1 最近的 0，我们更新对应 1 位置上的答案距离。然后从下一个 1 开始进行广度优先搜索。

这样做每次进行广度优先搜索的时间复杂度为 $O(m \times n)$ 。对于 $m \times n$ 个节点来说，每个节点可能都要进行一次广度优先搜索，总的时间复杂度为 $O(m^2 \times n^2)$ 。时间复杂度太高了。

我们可以换个角度：求每个 0 到 1 的最短曼哈顿距离（和求每个 1 到 0 是等价的）。

我们将所有值为 0 的元素位置保存到队列中，然后对所有值为 0 的元素开始进行广度优先搜索，每搜一步距离加 1，当每次搜索到 1 时，就可以得到 0 到这个 1 的最短距离，也就是当前离这个 1 最近的 0 的距离。

这样对于所有节点来说，总共需要进行一次广度优先搜索就可以了，时间复杂度为 $O(m \times n)$ 。

具体步骤如下：

使用一个集合变量 visited 存储所有值为 0 的元素坐标。使用队列变量 queue 存储所有值为 0 的元素坐标。使用二维数组 res 存储对应位置元素（即 $mat[i][j]$ ）到最近的 $0$ 的距离。
我们从所有为如果队列 queue 不为空，则从队列中依次取出值为 0 的元素坐标，遍历其上、下、左、右位置。
如果相邻区域未被访问过（说明遇到了值为 1 的元素），则更新相邻位置的距离值，并把相邻位置坐标加入队列 queue 和访问集合 visited 中。
继续执行 2 ~ 3 步，直到队列为空时，返回 res。

思路 1：代码

import collections

class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        rows, cols = len(mat), len(mat[0])
        res = [[0 for _ in range(cols)] for _ in range(rows)]
        visited = set()

        for i in range(rows):
            for j in range(cols):
                if mat[i][j] == 0:
                    visited.add((i, j))
        
        directions = {(1, 0), (-1, 0), (0, 1), (0, -1)}
        queue = collections.deque(visited)

        while queue:
            i, j = queue.popleft()
            for direction in directions:
                new_i = i + direction[0]
                new_j = j + direction[1]
                if 0 <= new_i < rows and 0 <= new_j < cols and (new_i, new_j) not in visited:
                    res[new_i][new_j] = res[i][j] + 1
                    queue.append((new_i, new_j))
                    visited.add((new_i, new_j))
        return res

思路 1：复杂度分析

时间复杂度： $O(m \times n)$ 。
空间复杂度： $O(m \times n)$ 。