0576. 出界的路径数

• 标签：动态规划
• 难度：中等

题目链接

• 0576. 出界的路径数 - 力扣

题目大意

描述：有一个大小为 $m \times n$ 的网络和一个球。球的起始位置为 $(startRow, startColumn)$。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。最多可以移动 $maxMove$ 次球。

现在给定五个整数 $m$、$n$、$maxMove$、$startRow$ 以及 $startColumn$。

要求：找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 $10^9 + 7$ 取余后的结果。

说明：

• $1 \le m, n \le 50$。
• $0 \le maxMove \le 50$。
• $0 \le startRow < m$。
• $0 \le startColumn < n$。

示例：

• 示例 1：

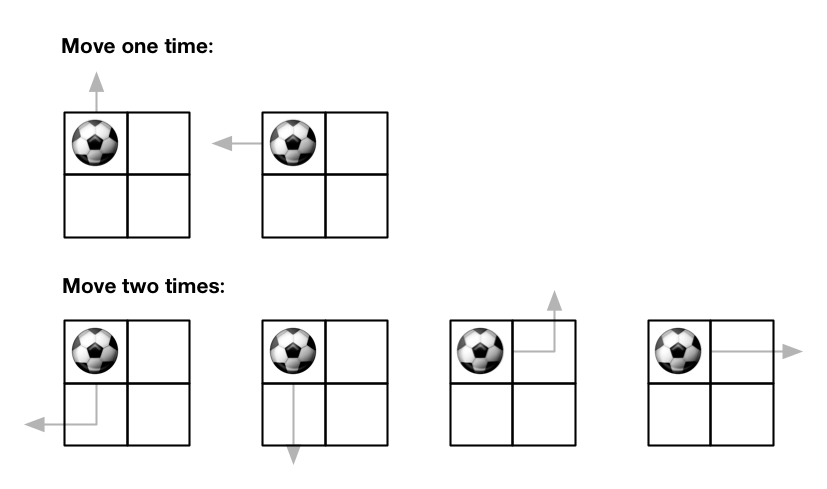
输入：m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
输出：6

解题思路

思路 1：记忆化搜索

1. 问题的状态定义为：从位置 $(i, j)$ 出发，最多使用 $moveCount$ 步，可以将球移出边界的路径数量。
2. 定义一个 $m \times n \times (maxMove + 1)$ 的三维数组 $memo$ 用于记录已经计算过的路径数量。
3. 定义递归函数 $dfs(i, j, moveCount)$ 用于计算路径数量。
   1. 如果 $(i, j)$ 已经出界，则说明找到了一条路径，返回方案数为 $1$。
   2. 如果没有移动次数了，则返回方案数为 $0$。
   3. 定义方案数 $ans$，遍历四个方向，递归计算四个方向的方案数，累积到 $ans$ 中，并进行取余。
   4. 返回方案数 $ans$。
4. 调用递归函数 $dfs(startRow, startColumn, maxMove)$，并将其返回值作为答案进行返回。

思路 1：代码

class Solution:
    def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
        directions = {(1, 0), (-1, 0), (0, 1), (0, -1)}
        mod = 10 ** 9 + 7

        memo = [[[-1 for _ in range(maxMove + 1)] for _ in range(n)] for _ in range(m)]

        def dfs(i, j, moveCount):
            if i < 0 or i >= m or j < 0 or j >= n:
                return 1
            
            if moveCount == 0:
                return 0

            if memo[i][j][moveCount] != -1:
                return memo[i][j][moveCount]

            ans = 0
            for direction in directions:
                new_i = i + direction[0]
                new_j = j + direction[1]
                ans += dfs(new_i, new_j, moveCount - 1)
                ans %= mod

            memo[i][j][moveCount] = ans
            return ans

        return dfs(startRow, startColumn, maxMove)

思路 1：复杂度分析

• 时间复杂度：$O(m \times n \times maxMove)$。
• 空间复杂度：$O(m \times n \times maxMove)$。

思路 2：动态规划

我们需要统计从 $(startRow, startColumn)$ 位置出发，最多移动 $maxMove$ 次能够穿过边界的所有路径数量。则我们可以根据位置和移动步数来划分阶段和定义状态。

1. 划分阶段

按照位置进行阶段划分。

2. 定义状态

定义状态 $dp[i][j][k]$ 表示为：从位置 $(i, j)$ 最多移动 $k$ 次最终穿过边界的所有路径数量。

3. 状态转移方程

因为球可以在上下左右四个方向上进行移动，所以对于位置 $(i, j)$，最多移动 $k$ 次最终穿过边界的所有路径数量取决于周围四个方向上最多经过 $k - 1$ 次穿过对应位置上的所有路径数量和。

即：$dp[i][j][k] = dp[i - 1][j][k - 1] + dp[i + 1][j][k - 1] + dp[i][j - 1][k - 1] + dp[i][j + 1][k - 1]$。

4. 初始条件

如果位置 $[i, j]$ 已经处于边缘，只差一步就穿过边界。则此时位置 $(i, j)$ 最多移动 $k$ 次最终穿过边界的所有路径数量取决于有相邻多少个方向是边界。也可以通过对上面 $(i - 1, j)$、$(i + 1, j)$、$(i, j - 1)$、$(i, j + 1)$ 是否已经穿过边界进行判断（每一个方向穿过一次，就累积一次），来计算路径数目。然后将其作为初始条件。

5. 最终结果

根据我们之前定义的状态，$dp[i][j][k]$ 表示为：从位置 $(i, j)$ 最多移动 $k$ 次最终穿过边界的所有路径数量。则最终答案为 $dp[startRow][startColumn][maxMove]$。

思路 2：动态规划代码

class Solution:
    def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
        directions = {(1, 0), (-1, 0), (0, 1), (0, -1)}
        mod = 10 ** 9 + 7
        
        dp = [[[0 for _ in range(maxMove + 1)] for _ in range(n)] for _ in range(m)]
        for i in r
        for k in range(1, maxMove + 1):
            for i in range(m):
                for j in range(n):
                    for direction in directions:
                        new_i = i + direction[0]
                        new_j = j + direction[1]
                        if 0 <= new_i < m and 0 <= new_j < n:
                            dp[i][j][k] = (dp[i][j][k] + dp[new_i][new_j][k - 1]) % mod
                        else:
                            dp[i][j][k] = (dp[i][j][k] + 1) % mod
        
        return dp[startRow][startColumn][maxMove]

思路 2：复杂度分析

• 时间复杂度：$O(m \times n \times maxMove)$。三重循环遍历的时间复杂度为 $O(m \times n \times maxMove)$。
• 空间复杂度：$O(m \times n \times maxMove)$。使用了三维数组保存状态，所以总体空间复杂度为 $O(m \times n \times maxMove)$。