0687. 最长同值路径

• 标签：树、深度优先搜索、二叉树
• 难度：中等

题目链接

• 0687. 最长同值路径 - 力扣

题目大意

描述：给定一个二叉树的根节点 $root$。

要求：返回二叉树中最长的路径的长度，该路径中每个节点具有相同值。 这条路径可以经过也可以不经过根节点。

说明：

• 树的节点数的范围是 $[0, 10^4]$。
• $-1000 \le Node.val \le 1000$。
• 树的深度将不超过 $1000$。
• 两个节点之间的路径长度：由它们之间的边数表示。

示例：

• 示例 1：

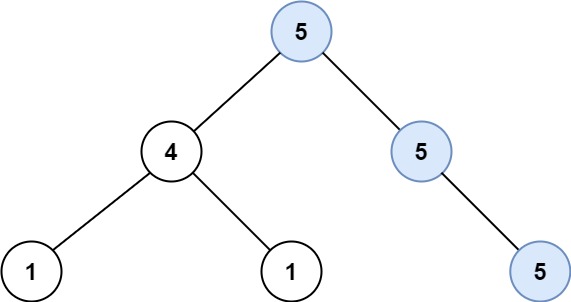
输入：root = [5,4,5,1,1,5]
输出：2

• 示例 2：

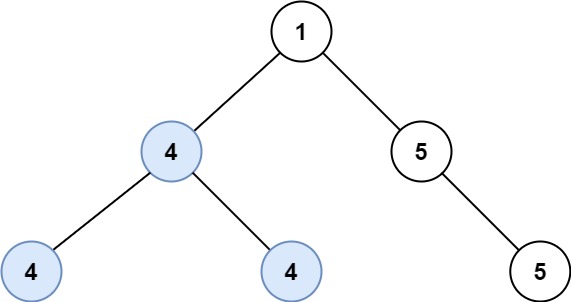
输入：root = [1,4,5,4,4,5]
输出：2

解题思路

思路 1：树形 DP + 深度优先搜索

这道题如果先不考虑「路径中每个节点具有相同值」这个条件，那么这道题就是在求「二叉树的直径长度（最长路径的长度）」。

「二叉树的直径长度」的定义为：二叉树中任意两个节点路径长度中的最大值。并且这条路径可能穿过也可能不穿过根节点。

对于根为 $root$ 的二叉树来说，其直径长度并不简单等于「左子树高度」加上「右子树高度」。

根据路径是否穿过根节点，我们可以将二叉树分为两种：

1. 直径长度所对应的路径穿过根节点，这种情况下：$\text{二叉树的直径} = \text{左子树高度} + \text{右子树高度}$。
2. 直径长度所对应的路径不穿过根节点，这种情况下：$\text{二叉树的直径} = \text{所有子树中最大直径长度}$。

也就是说根为 $root$ 的二叉树的直径长度可能来自于 $\text{左子树高度} + \text{右子树高度}$，也可能来自于 $\text{子树中的最大直径}$，即 $\text{二叉树的直径} = max(\text{左子树高度} + \text{右子树高度}, \quad \text{所有子树中最大直径长度})$。

那么现在问题就变成为如何求「子树的高度」和「子树中的最大直径」。

1. 子树的高度：我们可以利用深度优先搜索方法，递归遍历左右子树，并分别返回左右子树的高度。
2. 子树中的最大直径：我们可以在递归求解子树高度的时候维护一个 $ans$ 变量，用于记录所有 $\text{左子树高度} + \text{右子树高度}$ 中的最大值。

最终 $ans$ 就是我们所求的该二叉树的最大直径。

接下来我们再来加上「路径中每个节点具有相同值」这个限制条件。

1. 「左子树高度」应变为「左子树最长同值路径长度」。
2. 「右子树高度」应变为「右子树最长同值路径长度」。
3. 题目变为求「二叉树的最长同值路径长度」，式子为：$\text{二叉树的最长同值路径长度} = max(\text{左子树最长同值路径长度} + \text{右子树最长同值路径长度}, \quad \text{所有子树中最长同值路径长度})$。

在递归遍历的时候，我们还需要当前节点与左右子节点的值的相同情况，来维护更新「包含当前节点的最长同值路径长度」。

1. 在递归遍历左子树时，如果当前节点与左子树的值相同，则：$\text{包含当前节点向左的最长同值路径长度} = \text{左子树最长同值路径长度} + 1$，否则为 $0$。
2. 在递归遍历左子树时，如果当前节点与左子树的值相同，则：$\text{包含当前节点向右的最长同值路径长度} = \text{右子树最长同值路径长度} + 1$，否则为 $0$。

则：$\text{包含当前节点向左的最长同值路径长度} = max(\text{包含当前节点向左的最长同值路径长度}, \quad \text{包含当前节点向右的最长同值路径长度})$。

思路 1：代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.ans = 0

    def dfs(self, node):
        if not node:
            return 0

        left_len = self.dfs(node.left)          # 左子树高度
        right_len = self.dfs(node.right)        # 右子树高度
        if node.left and node.left.val == node.val:
            left_len += 1
        else:
            left_len = 0
        if node.right and node.right.val == node.val:
            right_len += 1
        else:
            right_len = 0
        self.ans = max(self.ans, left_len + right_len)
        return max(left_len, right_len)

    def longestUnivaluePath(self, root: Optional[TreeNode]) -> int:
        self.dfs(root)

        return self.ans

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 为二叉树的节点个数。
• 空间复杂度：$O(n)$。