0695. 岛屿的最大面积

• 标签：深度优先搜索、广度优先搜索、并查集、数组、矩阵
• 难度：中等

题目链接

• 0695. 岛屿的最大面积 - 力扣

题目大意

描述：给定一个只包含 $0$、$1$ 元素的二维数组，$1$ 代表岛屿，$0$ 代表水。一座岛的面积就是上下左右相邻的 $1$ 所组成的连通块的数目。

要求：计算出最大的岛屿面积。

说明：

• $m == grid.length$。
• $n == grid[i].length$。
• $1 \le m, n \le 50$。
• $grid[i][j]$ 为 $0$ 或 $1$。

示例：

• 示例 1：

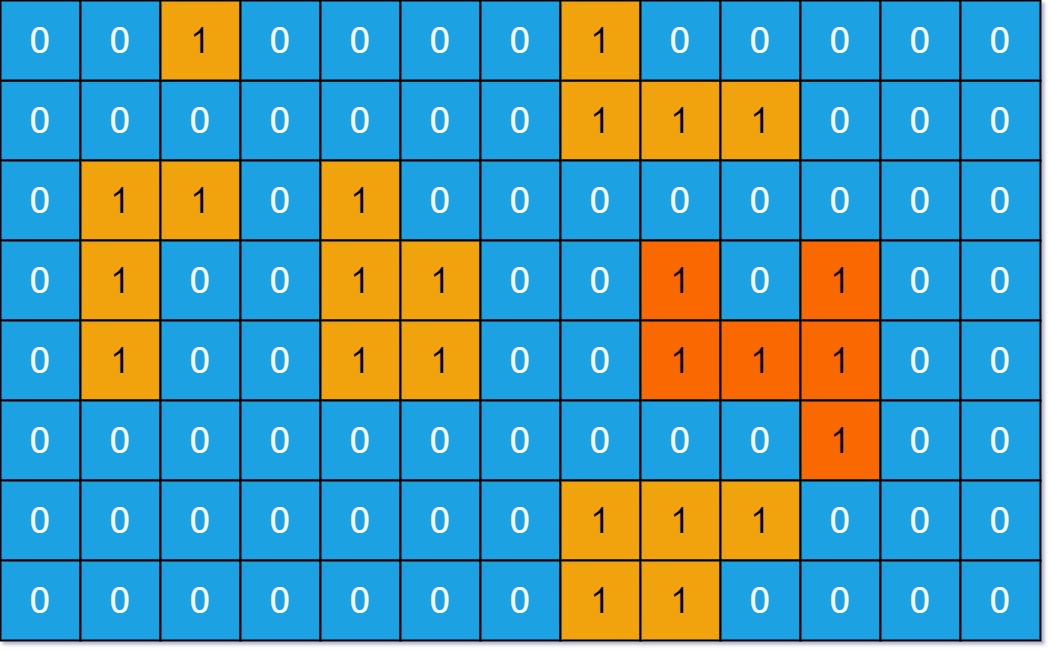
输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

• 示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

解题思路

思路 1：深度优先搜索

1. 遍历二维数组的每一个元素，对于每个值为 $1$ 的元素：
   1. 将该位置上的值置为 $0$（防止二次重复计算）。
   2. 递归搜索该位置上下左右四个位置，并统计搜到值为 $1$ 的元素个数。
   3. 返回值为 $1$ 的元素个数（即为该岛的面积）。
2. 维护并更新最大的岛面积。
3. 返回最大的到面积。

思路 1：代码

class Solution:
    def dfs(self, grid, i, j):
        n = len(grid)
        m = len(grid[0])
        if i < 0 or i >= n or j < 0 or j >= m or grid[i][j] == 0:
            return 0
        ans = 1
        grid[i][j] = 0
        ans += self.dfs(grid, i + 1, j)
        ans += self.dfs(grid, i, j + 1)
        ans += self.dfs(grid, i - 1, j)
        ans += self.dfs(grid, i, j - 1)
        return ans

    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        ans = 0
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if grid[i][j] == 1:
                    ans = max(ans, self.dfs(grid, i, j))
        return ans

思路 1：复杂度分析

• 时间复杂度：$O(n \times m)$，其中 $m$ 和 $n$ 分别为行数和列数。
• 空间复杂度：$O(n \times m)$。

思路 2：广度优先搜索

1. 使用 $ans$ 记录最大岛屿面积。
2. 遍历二维数组的每一个元素，对于每个值为 $1$ 的元素：
   1. 将该元素置为 $0$。并使用队列 $queue$ 存储该节点位置。使用 $temp\underline{\hspace{0.5em}}ans$ 记录当前岛屿面积。
   2. 然后从队列 $queue$ 中取出第一个节点位置 $(i, j)$。遍历该节点位置上、下、左、右四个方向上的相邻节点。并将其置为 $0$（避免重复搜索）。并将其加入到队列中。并累加当前岛屿面积，即 temp_ans += 1。
   3. 不断重复上一步骤，直到队列 $queue$ 为空。
   4. 更新当前最大岛屿面积，即 ans = max(ans, temp_ans)。
3. 将 $ans$ 作为答案返回。

思路 2：代码

import collections

class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        directs = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        rows, cols = len(grid), len(grid[0])
        ans = 0
        for i in range(rows):
            for j in range(cols):
                if grid[i][j] == 1:
                    grid[i][j] = 0
                    temp_ans = 1
                    q = collections.deque([(i, j)])
                    while q:
                        i, j = q.popleft()
                        for direct in directs:
                            new_i = i + direct[0]
                            new_j = j + direct[1]
                            if new_i < 0 or new_i >= rows or new_j < 0 or new_j >= cols or grid[new_i][new_j] == 0:
                                continue
                            grid[new_i][new_j] = 0
                            q.append((new_i, new_j))
                            temp_ans += 1

                    ans = max(ans, temp_ans)
        return ans

思路 2：复杂度分析

• 时间复杂度：$O(n \times m)$，其中 $m$ 和 $n$ 分别为行数和列数。
• 空间复杂度：$O(n \times m)$。