0778. 水位上升的泳池中游泳

ITCharge大约 3 分钟

0778. 水位上升的泳池中游泳

标签：深度优先搜索、广度优先搜索、并查集、数组、二分查找、矩阵、堆（优先队列）
难度：困难

题目链接

0778. 水位上升的泳池中游泳 - 力扣

题目大意

描述：给定一个 $n \times n$ 大小的二维数组 $grid$ ，每一个方格的值 $grid[i][j]$ 表示为位置 $(i, j)$ 的高度。

现在要从左上角 $(0, 0)$ 位置出发，经过方格的一些点，到达右下角 $(n - 1, n - 1)$ 位置上。其中所经过路径的花费为这条路径上所有位置的最大高度。

要求：计算从 $(0, 0)$ 位置到 $(n - 1, n - 1)$ 的最优路径的花费。

说明：

最优路径：路径上最大高度最小的那条路径。
$n == grid.length$ 。
$n == grid[i].length$ 。
$1 \le n \le 50$ 。
$0 \le grid[i][j] < n2$ 。
$grid[i][j]$ 中每个值均无重复。

示例：

示例 1：

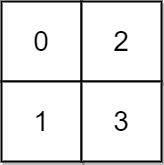
输入: grid = [[0,2],[1,3]]
输出: 3
解释:
时间为 0 时，你位于坐标方格的位置为 (0, 0)。
此时你不能游向任意方向，因为四个相邻方向平台的高度都大于当前时间为 0 时的水位。
等时间到达 3 时，你才可以游向平台 (1, 1). 因为此时的水位是 3，坐标方格中的平台没有比水位 3 更高的，所以你可以游向坐标方格中的任意位置。

示例 2：

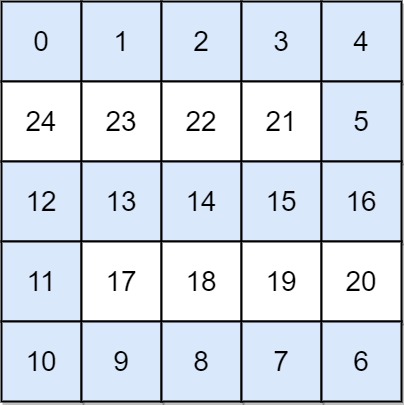
输入: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
输出: 16
解释: 最终的路线用加粗进行了标记。
我们必须等到时间为 16，此时才能保证平台 (0, 0) 和 (4, 4) 是连通的。

解题思路

思路 1：并查集

将整个网络抽象为一个无向图，每个点与相邻的点（上下左右）之间都存在一条无向边，边的权重为两个点之间的最大高度。

我们要找到左上角到右下角的最优路径，可以遍历所有的点，将所有的边存储到数组中，每条边的存储格式为 $[x, y, h]$ ，意思是编号 $x$ 的点和编号为 $y$ 的点之间的权重为 $h$ 。

然后按照权重从小到大的顺序，对所有边进行排序。

再按照权重大小遍历所有边，将其依次加入并查集中。并且每次都需要判断 $(0, 0)$ 点和 $(n - 1, n - 1)$ 点是否连通。

如果连通，则该边的权重即为答案。

思路 1：代码

class UnionFind:

    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.count = n

    def find(self, x):
        while x != self.parent[x]:
            self.parent[x] = self.parent[self.parent[x]]
            x = self.parent[x]
        return x

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return

        self.parent[root_x] = root_y
        self.count -= 1

    def is_connected(self, x, y):
        return self.find(x) == self.find(y)

class Solution:
    def swimInWater(self, grid: List[List[int]]) -> int:
        row_size = len(grid)
        col_size = len(grid[0])
        size = row_size * col_size
        edges = []
        for row in range(row_size):
            for col in range(col_size):
                if row < row_size - 1:
                    x = row * col_size + col
                    y = (row + 1) * col_size + col
                    h = max(grid[row][col], grid[row + 1][col])
                    edges.append([x, y, h])
                if col < col_size - 1:
                    x = row * col_size + col
                    y = row * col_size + col + 1
                    h = max(grid[row][col], grid[row][col + 1])
                    edges.append([x, y, h])

        edges.sort(key=lambda x: x[2])

        union_find = UnionFind(size)

        for edge in edges:
            x, y, h = edge[0], edge[1], edge[2]
            union_find.union(x, y)
            if union_find.is_connected(0, size - 1):
                return h
        return 0

思路 1：复杂度分析

时间复杂度： $O(m \times n \times \alpha(m \times n))$ ，其中 $\alpha$ 是反 Ackerman 函数。
空间复杂度： $O(m \times n)$ 。