0766. 托普利茨矩阵

• 标签：数组、矩阵
• 难度：简单

题目链接

• 0766. 托普利茨矩阵 - 力扣

题目大意

描述：给定一个 $m \times n$ 大小的矩阵 $matrix$。

要求：如果 $matrix$ 是托普利茨矩阵，则返回 True；否则返回 False。

说明：

• 托普利茨矩阵：矩阵上每一条由左上到右下的对角线上的元素都相同。
• $m == matrix.length$。
• $n == matrix[i].length$。
• $1 \le m, n \le 20$。
• $0 \le matrix[i][j] \le 99$。

示例：

• 示例 1：

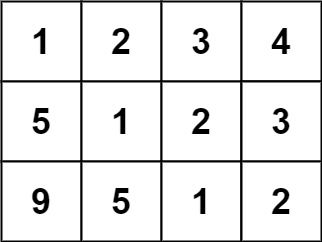
输入：matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
输出：true
解释：
在上述矩阵中, 其对角线为: 
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]"。 
各条对角线上的所有元素均相同, 因此答案是 True。

• 示例 2：

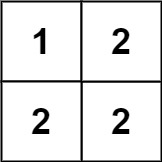
输入：matrix = [[1,2],[2,2]]
输出：false
解释：
对角线 "[1, 2]" 上的元素不同。

解题思路

思路 1：简单模拟

1. 两层循环遍历矩阵，依次判断矩阵当前位置 $(i, j)$ 上的值 $matrix[i][j]$ 与其左上角位置 $(i - 1, j - 1)$ 位置上的值 $matrix[i - 1][j - 1]$ 是否相等。
2. 如果不相等，则返回 False。
3. 遍历完，则返回 True。

思路 1：代码

class Solution:
    def isToeplitzMatrix(self, matrix: List[List[int]]) -> bool:
        for i in range(1, len(matrix)):
            for j in range(1, len(matrix[0])):
                if matrix[i][j] != matrix[i - 1][j - 1]:
                    return False
        return True

思路 1：复杂度分析

• 时间复杂度：$O(m \times n)$，其中 $m$、$n$ 分别是矩阵 $matrix$ 的行数、列数。
• 空间复杂度：$O(m \times n)$。