0850. 矩形面积 II
大约 3 分钟
0850. 矩形面积 II
- 标签:线段树、数组、有序集合、扫描线
- 难度:困难
题目链接
题目大意
描述:给定一个二维矩形列表 rectangles,其中 rectangle[i] = [x1, y1, x2, y2] 表示第 i 个矩形,(x1, y1) 是第 i 个矩形左下角的坐标,(x2, y2) 是第 i 个矩形右上角的坐标。。
要求:计算 rectangles 中所有矩形所覆盖的总面积,并返回总面积。
说明:
- 任何被两个或多个矩形覆盖的区域应只计算一次 。
- 因为答案可能太大,返回 的模。
- 。
- 。
- 。
- 矩形叠加覆盖后的总面积不会超越 ,这意味着可以用一个 位有符号整数来保存面积结果。
示例:
- 示例 1:
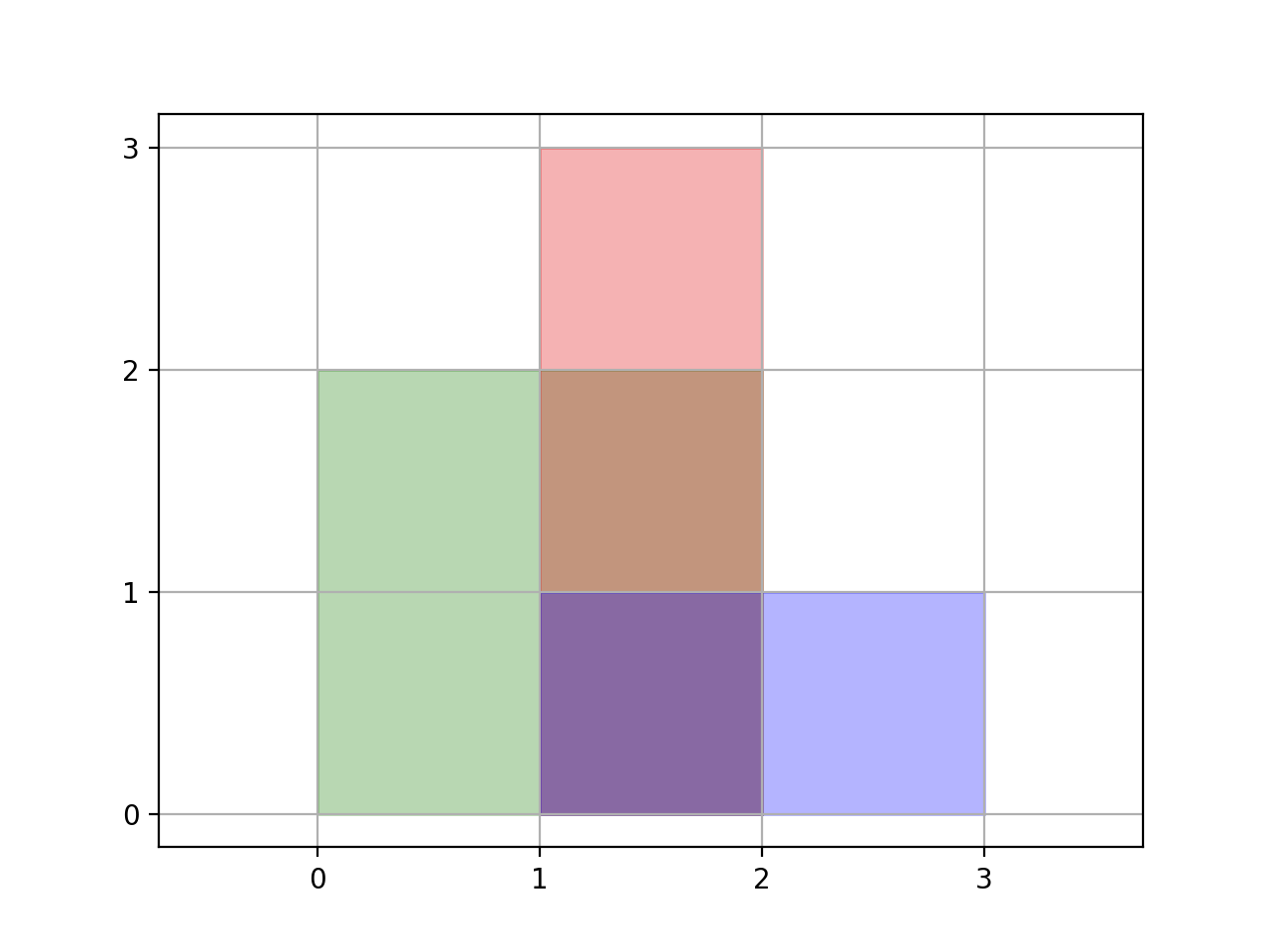
输入:rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出:6
解释:如图所示,三个矩形覆盖了总面积为6的区域。
从 (1,1) 到 (2,2),绿色矩形和红色矩形重叠。
从 (1,0) 到 (2,3),三个矩形都重叠。
解题思路
思路 1:扫描线 + 动态开点线段树
思路 1:扫描线 + 动态开点线段树代码
# 线段树的节点类
class SegTreeNode:
def __init__(self, left=-1, right=-1, cnt=0, height=0, leftNode=None, rightNode=None):
self.left = left # 区间左边界
self.right = right # 区间右边界
self.mid = left + (right - left) // 2
self.leftNode = leftNode # 区间左节点
self.rightNode = rightNode # 区间右节点
self.cnt = cnt # 节点值(区间值)
self.height = height # 区间问题的延迟更新标记
# 线段树类
class SegmentTree:
# 初始化线段树接口
def __init__(self):
self.tree = SegTreeNode(0, int(1e9))
# 区间更新接口:将区间为 [q_left, q_right] 上的元素值修改为 val
def update_interval(self, q_left, q_right, val):
self.__update_interval(q_left, q_right, val, self.tree)
# 区间查询接口:查询区间为 [q_left, q_right] 的区间值
def query_interval(self, q_left, q_right):
return self.__query_interval(q_left, q_right, self.tree)
# 以下为内部实现方法
# 区间更新实现方法
def __update_interval(self, q_left, q_right, val, node):
if node.right < q_left or node.left > q_right: # 节点所在区间与 [q_left, q_right] 无关
return
if node.left >= q_left and node.right <= q_right: # 节点所在区间被 [q_left, q_right] 所覆盖
node.cnt += val # 当前节点所在区间每个元素值改为 val
self.__pushup(node)
return
self.__pushdown(node)
if q_left <= node.mid: # 在左子树中更新区间值
self.__update_interval(q_left, q_right, val, node.leftNode)
if q_right > node.mid: # 在右子树中更新区间值
self.__update_interval(q_left, q_right, val, node.rightNode)
self.__pushup(node)
# 区间查询实现方法:在线段树的 [left, right] 区间范围中搜索区间为 [q_left, q_right] 的区间值
def __query_interval(self, q_left, q_right, node):
if node.right < q_left or node.left > q_right: # 节点所在区间与 [q_left, q_right] 无关
return 0
if node.left >= q_left and node.right <= q_right: # 节点所在区间被 [q_left, q_right] 所覆盖
return node.height # 直接返回节点值
self.__pushdown(node)
res_left = 0 # 左子树查询结果
res_right = 0 # 右子树查询结果
if q_left <= node.mid: # 在左子树中查询
res_left = self.__query_interval(q_left, node.mid, node.leftNode)
if q_right > node.mid: # 在右子树中查询
res_right = self.__query_interval(node.mid + 1, q_right, node.rightNode)
return res_left + res_right # 返回左右子树元素值的聚合计算结果
# 向上更新实现方法:更新 node 节点区间值 等于 该节点左右子节点元素值的聚合计算结果
def __pushup(self, node):
if node.cnt > 0:
node.height = node.right - node.left + 1
else:
if node.leftNode and node.rightNode:
node.height = node.leftNode.height + node.rightNode.height
else:
node.height = 0
# 向下更新实现方法:更新 node 节点所在区间的左右子节点的值和懒惰标记
def __pushdown(self, node):
if node.leftNode is None:
node.leftNode = SegTreeNode(node.left, node.mid)
if node.rightNode is None:
node.rightNode = SegTreeNode(node.mid + 1, node.right)
class Solution:
def rectangleArea(self, rectangles) -> int:
# lines 存储每个矩阵的上下两条边
lines = []
for rectangle in rectangles:
x1, y1, x2, y2 = rectangle
lines.append([x1, y1 + 1, y2, 1])
lines.append([x2, y1 + 1, y2, -1])
lines.sort(key=lambda line: line[0])
# 建立线段树
self.STree = SegmentTree()
ans = 0
mod = 10 ** 9 + 7
prev_x = lines[0][0]
for i in range(len(lines)):
x, y1, y2, val = lines[i]
height = self.STree.query_interval(0, int(1e9))
ans += height * (x - prev_x)
ans %= mod
self.STree.update_interval(y1, y2, val)
prev_x = x
return ans