0892. 三维形体的表面积

• 标签：几何、数组、数学、矩阵
• 难度：简单

题目链接

• 0892. 三维形体的表面积 - 力扣

题目大意

描述：给定一个 $n \times n$ 的网格 $grid$，上面放置着一些 $1 \times 1 \times 1$ 的正方体。每个值 $v = grid[i][j]$ 表示 $v$ 个正方体叠放在对应单元格 $(i, j)$ 上。

放置好正方体后，任何直接相邻的正方体都会互相粘在一起，形成一些不规则的三维形体。

要求：返回最终这些形体的总面积。

说明：

• 每个形体的底面也需要计入表面积中。

示例：

• 示例 1：

输入：grid = [[1,2],[3,4]]
输出：34

• 示例 2：

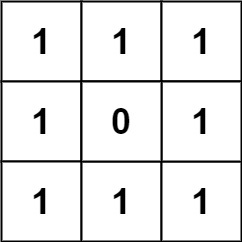
输入：grid = [[1,1,1],[1,0,1],[1,1,1]]
输出：32

解题思路

思路 1：模拟

使用二重循环遍历所有的正方体，计算每一个正方体所贡献的表面积，将其累积起来即为答案。

而每一个正方体所贡献的表面积，可以通过枚举当前正方体前后左右相邻四个方向上的正方体的个数，从而通过判断计算得出。

• 如果当前位置 $(row, col)$ 存在正方体，则正方体在上下位置上起码贡献了 $2$ 的表面积。
• 如果当前位置 $(row, col)$ 的相邻位置 $(new\underline{}row, new\underline{}col)$ 上不存在正方体，说明当前正方体在该方向为最外侧，则 $(row, col)$ 位置所贡献的表面积为当前位置上的正方体个数，即 $grid[row][col]$。
• 如果当前位置 $(row, col)$ 的相邻位置 $(new\underline{}row, new\underline{}col)$ 上存在正方体：
  • 如果 $grid[row][col] > grid[new\underline{}row][new\underline{}col]$，说明 $grid[row][col]$ 在该方向上底面一部分被 $grid[new\underline{}row][new\underline{}col]$ 遮盖了，则 $(row, col)$ 位置所贡献的表面积为 $grid[row][col] - grid[new_row][new_col]$。
  • 如果 $grid[row][col] \le grid[new\underline{}row][new\underline{}col]$，说明 $grid[row][col]$ 在该方向上完全被 $grid[new\underline{}row][new\underline{}col]$ 遮盖了，则 $(row, col)$ 位置所贡献的表面积为 $0$。

思路 1：代码

class Solution:
    def surfaceArea(self, grid: List[List[int]]) -> int:
        directions = [(-1, 0), (0, 1), (1, 0), (0, -1)]
        size = len(grid)

        ans = 0
        for row in range(size):
            for col in range(size):
                if grid[row][col]:
                    # 底部、顶部贡献表面积
                    ans += 2
                    for direction in directions:
                        new_row = row + direction[0]
                        new_col = col + direction[1]
                        if 0 <= new_row < size and 0 <= new_col < size:
                            if grid[row][col] > grid[new_row][new_col]:
                                add = grid[row][col] - grid[new_row][new_col]
                            else:
                                add = 0
                        else:
                            add = grid[row][col]
                        ans += add
        return ans

思路 1：复杂度分析

• 时间复杂度：$O(n^2)$，其中 $n$ 为二位数组 $grid$ 的行数或列数。
• 空间复杂度：$O(1)$。