0968. 监控二叉树

• 标签：树、深度优先搜索、动态规划、二叉树
• 难度：困难

题目链接

• 0968. 监控二叉树 - 力扣

题目大意

给定一个二叉树，需要在树的节点上安装摄像头。节点上的每个摄影头都可以监视其父节点、自身及其直接子节点。

计算监控树的所有节点所需的最小摄像头数量。

• 示例 1：

img

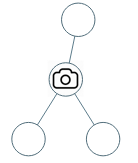
输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

• 示例 2：

img

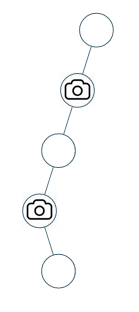
输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

解题思路

根据题意可知，一个摄像头的有效范围为 3 层：父节点、自身及其直接子节点。而约是下层的节点就越多，所以摄像头应该优先满足下层节点。可以使用后序遍历的方式遍历二叉树的节点，这样就可以优先遍历叶子节点。

对于每个节点，利用贪心思想，可以确定三种状态：

• 第一种状态：该节点无覆盖
• 第二种状态：该节点已经装上了摄像头
• 第三种状态：该节点已经覆盖

为了让摄像头数量最少，我们要尽量让叶⼦节点的⽗节点安装摄像头，这样才能摄像头的数量最少。对此我们应当分析当前节点和左右两侧子节点的覆盖情况。

先来考虑空节点，空节点应该算作已经覆盖状态。

再来考虑左右两侧子覆盖情况：

• 如果左节点或者右节点都无覆盖，则当前节点需要装上摄像头，答案 res 需要 + 1。
• 如果左节点已经覆盖或者右节点已经装上了摄像头，则当前节点已经覆盖。
• 如果左节点右节点都已经覆盖，则当前节点无覆盖。

根据以上条件就可以写出对应的后序遍历代码。

代码

class Solution:
    res = 0
    def traversal(self, cur: TreeNode) -> int:
        if not cur:
            return 3

        left = self.traversal(cur.left)
        right = self.traversal(cur.right)

        if left == 1 or right == 1:
            self.res += 1
            return 2

        if left == 2 or right == 2:
            return 3

        if left == 3 and right == 3:
            return 1
        return -1

    def minCameraCover(self, root: TreeNode) -> int:
        self.res = 0
        if self.traversal(root) == 1:
            self.res += 1
        return self.res