0959. 由斜杠划分区域

• 标签：深度优先搜索、广度优先搜索、并查集、图
• 难度：中等

题目链接

• 0959. 由斜杠划分区域 - 力扣

题目大意

描述：在由 $1 \times 1$ 方格组成的 $n \times n$ 网格 $grid$ 中，每个 $1 \times 1$ 方块由 '/'、'\' 或 ' ' 构成。这些字符会将方块划分为一些共边的区域。

现在给定代表网格的二维数组 $grid$。

要求：返回区域的数目。

说明：

• 反斜杠字符是转义的，因此 '\' 用 '\\' 表示。
• $n == grid.length == grid[i].length$。
• $1 \le n \le 30$。
• $grid[i][j]$ 是 '/'、'\' 或 ' '。

示例：

• 示例 1：

输入：grid = [" /","/ "]
输出：2

• 示例 2：

输入：grid = ["/\\","\\/"]
输出：5
解释：回想一下，因为 \ 字符是转义的，所以 "/\\" 表示 /\，而 "\\/" 表示 \/。

解题思路

思路 1：并查集

我们把一个 $1 \times 1$ 的单元格分割成逻辑上的 $4$ 个部分，则 ' '、'/'、'\' 可以将 $1 \times 1$ 的方格分割为以下三种形态：

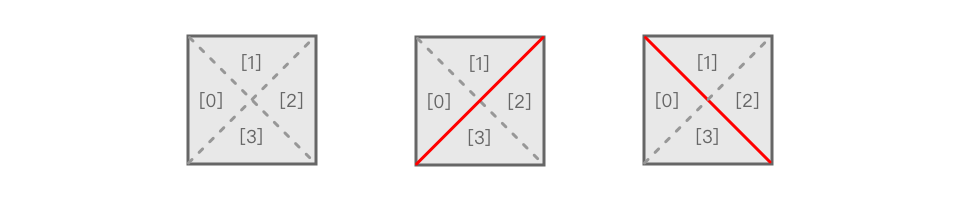
在进行遍历的时候，需要将联通的部分进行合并，并统计出联通的块数。这就需要用到了并查集。

遍历二维数组 $gird$，然后在「单元格内」和「单元格间」进行合并。

现在我们为单元格的每个小三角部分按顺时针方向都编上编号，起始位置为左边。然后单元格间的编号按照从左到右，从上到下的位置进行编号，如下图所示：

假设当前单元格的起始位置为 $index$，则合并策略如下：

• 如果是单元格内：
  • 如果是空格：合并 $index$、$index + 1$、$index + 2$、$index + 3$。
  • 如果是 '/'：合并 $index$ 和 $index + 1$，合并 $index + 2$ 和 $index + 3$。
  • 如果是 '\'：合并 $index$ 和 $index + 3$，合并 $index + 1$ 和 $index + 2$。
• 如果是单元格间，则向下向右进行合并：
  • 向下：合并 $index + 3$ 和 $index + 4 * size + 1 $。
  • 向右：合并 $index + 2$ 和 $index + 4$。

最后合并完成之后，统计并查集中连通分量个数即为答案。

思路 1：代码

class UnionFind:

    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.count = n

    def find(self, x):
        while x != self.parent[x]:
            self.parent[x] = self.parent[self.parent[x]]
            x = self.parent[x]
        return x

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return

        self.parent[root_x] = root_y
        self.count -= 1

    def is_connected(self, x, y):
        return self.find(x) == self.find(y)

class Solution:
    def regionsBySlashes(self, grid: List[str]) -> int:
        size = len(grid)
        m = 4 * size * size
        union_find = UnionFind(m)
        for i in range(size):
            for j in range(size):
                index = 4 * (i * size + j)
                ch = grid[i][j]
                if ch == '/':
                    union_find.union(index, index + 1)
                    union_find.union(index + 2, index + 3)
                elif ch == '\\':
                    union_find.union(index, index + 3)
                    union_find.union(index + 1, index + 2)
                else:
                    union_find.union(index, index + 1)
                    union_find.union(index + 1, index + 2)
                    union_find.union(index + 2, index + 3)
                if j + 1 < size:
                    union_find.union(index + 2, index + 4)
                if i + 1 < size:
                    union_find.union(index + 3, index + 4 * size + 1)

        return union_find.count

思路 1：复杂度分析

• 时间复杂度：$O(n^2 \times \alpha(n^2))$，其中 $\alpha$ 是反 Ackerman 函数。
• 空间复杂度：$O(n^2)$。