1039. 多边形三角剖分的最低得分

• 标签：数组、动态规划
• 难度：中等

题目链接

• 1039. 多边形三角剖分的最低得分 - 力扣

题目大意

描述：有一个凸的 $n$ 边形，其每个顶点都有一个整数值。给定一个整数数组 $values$，其中 $values[i]$ 是第 $i$ 个顶点的值（即顺时针顺序）。

现在要将 $n$ 边形剖分为 $n - 2$ 个三角形，对于每个三角形，该三角形的值是顶点标记的乘积，$n$ 边形三角剖分的分数是进行三角剖分后所有 $n - 2$ 个三角形的值之和。

要求：返回多边形进行三角剖分可以得到的最低分。

说明：

• $n == values.length$。
• $3 \le n \le 50$。
• $1 \le values[i] \le 100$。

示例：

• 示例 1：

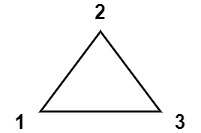
输入：values = [1,2,3]
输出：6
解释：多边形已经三角化，唯一三角形的分数为 6。

• 示例 2：

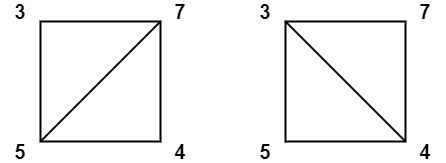
输入：values = [3,7,4,5]
输出：144
解释：有两种三角剖分，可能得分分别为：3*7*5 + 4*5*7 = 245，或 3*4*5 + 3*4*7 = 144。最低分数为 144。

解题思路

思路 1：动态规划

对于 $0 \sim n - 1$ 个顶点组成的凸多边形进行三角剖分，我们可以在 $[0, n - 1]$ 中任选 $1$ 个点 $k$，从而将凸多边形划分为：

1. 顶点 $0 \sim k$ 组成的凸多边形。
2. 顶点 $0$、$k$、$n - 1$ 组成的三角形。
3. 顶点 $k \sim n - 1$ 组成的凸多边形。

对于顶点 $0$、$k$、$n - 1$ 组成的三角形，我们可以直接计算对应的三角剖分分数为 $values[0] \times values[k] \times values[n - 1]$。

而对于顶点 $0 \sim k$ 组成的凸多边形和顶点 $k \sim n - 1$ 组成的凸多边形，我们可以利用递归或者动态规划的思想，定义一个 $dp[i][j]$ 用于计算顶点 $i$ 到顶点 $j$ 组成的多边形三角剖分的最小分数。

具体做法如下：

1. 划分阶段

按照区间长度进行阶段划分。

2. 定义状态

定义状态 $dp[i][j]$ 表示为：区间 $[i, j]$ 内三角剖分后的最小分数。

3. 状态转移方程

对于区间 $[i, j]$，枚举分割点 $k$，最小分数为 $min(dp[i][k] + dp[k][j] + values[i] \times values[k] \times values[j])$，即：$dp[i][j] = min(dp[i][k] + dp[k][j] + values[i] \times values[k] \times values[j])$。

4. 初始条件

• 默认情况下，所有区间 $[i, j]$ 的最小分数为无穷大。
• 当区间 $[i, j]$ 长度小于 $3$ 时，无法进行三角剖分，其最小分数为 $0$。
• 当区间 $[i, j]$ 长度等于 $3$ 时，其三角剖分的最小分数为 $values[i] * values[i + 1] * values[i + 2]$。

5. 最终结果

根据我们之前定义的状态，$dp[i][j]$ 表示为：区间 $[i, j]$ 内三角剖分后的最小分数。。 所以最终结果为 $dp[0][size - 1]$。

思路 1：代码

class Solution:
    def minScoreTriangulation(self, values: List[int]) -> int:
        size = len(values)
        dp = [[float('inf') for _ in range(size)] for _ in range(size)]
        for l in range(1, size + 1):
            for i in range(size):
                j = i + l - 1
                if j >= size:
                    break
                if l < 3:
                    dp[i][j] = 0
                elif l == 3:
                    dp[i][j] = values[i] * values[i + 1] * values[i + 2]
                else:
                    for k in range(i + 1, j):
                        dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + values[i] * values[j] * values[k])

        return dp[0][size - 1]

思路 1：复杂度分析

• 时间复杂度：$O(n^3)$，其中 $n$ 为顶点个数。
• 空间复杂度：$O(n^2)$。