1035. 不相交的线

• 标签：数组、动态规划
• 难度：中等

题目链接

• 1035. 不相交的线 - 力扣

题目大意

有两条独立平行的水平线，按照给定的顺序写下 nums1 和 nums2 的整数。

现在，我们可以绘制一些直线，只要满足以下要求：

• nums1[i] == nums2[j]。
• 绘制的直线不与其他任何直线相交。

例如：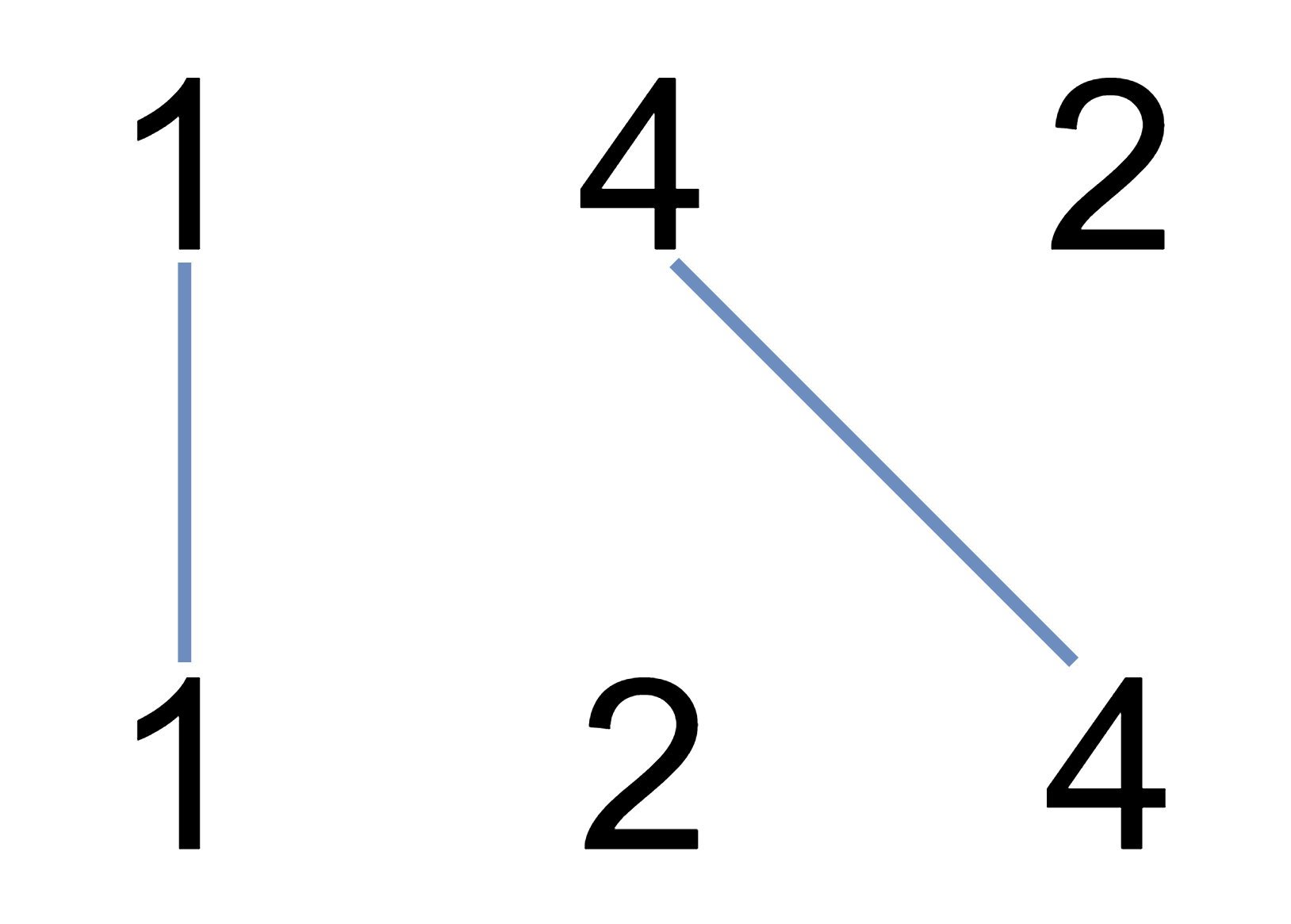

现在要求：计算出能绘制的最大直线数目。

解题思路

动态规划求解。

定义状态 dp[i][j] 表示：nums1 中前 i 个数与 nums2 中前 j 个数的最大连接数，则：

状态转移方程为：

• 如果 nums1[i] == nums[j]，则 nums1[i] 与 nums2[j] 可连线，此时 dp[i][j] = dp[i - 1][j - 1] + 1。
• 如果 nums1[i] != nums[j]，则 nums1[i] 与 nums2[j] 不可连线，此时最大连线数取决于 dp[i - 1][j] 和 dp[i][j - 1] 的较大值，即：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])。

最后输出 dp[size1][size2] 即可。

代码

class Solution:
    def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
        size1 = len(nums1)
        size2 = len(nums2)
        dp = [[0 for _ in range(size2 + 1)] for _ in range(size1 + 1)]
        for i in range(1, size1 + 1):
            for j in range(1, size2 + 1):
                if nums1[i - 1] == nums2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        return dp[size1][size2]