1161. 最大层内元素和

• 标签：树、深度优先搜索、广度优先搜索、二叉树
• 难度：中等

题目链接

• 1161. 最大层内元素和 - 力扣

题目大意

描述：给你一个二叉树的根节点 $root$。设根节点位于二叉树的第 $1$ 层，而根节点的子节点位于第 $2$ 层，依此类推。

要求：返回层内元素之和最大的那几层（可能只有一层）的层号，并返回其中层号最小的那个。

说明：

• 树中的节点数在 $[1, 10^4]$ 范围内。
• $-10^5 \le Node.val \le 10^5$。

示例：

• 示例 1：

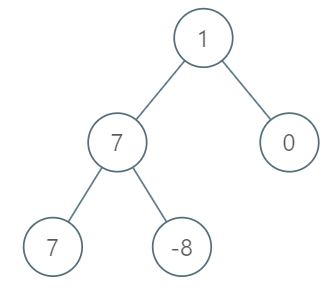
输入：root = [1,7,0,7,-8,null,null]
输出：2
解释：
第 1 层各元素之和为 1，
第 2 层各元素之和为 7 + 0 = 7，
第 3 层各元素之和为 7 + -8 = -1，
所以我们返回第 2 层的层号，它的层内元素之和最大。

• 示例 2：

输入：root = [989,null,10250,98693,-89388,null,null,null,-32127]
输出：2

解题思路

思路 1：二叉树的层序遍历

1. 利用广度优先搜索，在二叉树的层序遍历的基础上，统计每一层节点和，并存入数组 $levels$ 中。
2. 遍历 $levels$ 数组，从 $levels$ 数组中找到最大层和 $max\underline{}sum$。
3. 再次遍历 $levels$ 数组，找出等于最大层和 $max\underline{}sum$ 的那一层，并返回该层序号。

思路 1：代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        if not root:
            return []
        queue = [root]
        levels = []
        while queue:
            level = 0
            size = len(queue)
            for _ in range(size):
                curr = queue.pop(0)
                level += curr.val
                if curr.left:
                    queue.append(curr.left)
                if curr.right:
                    queue.append(curr.right)
            levels.append(level)
        return levels

    def maxLevelSum(self, root: Optional[TreeNode]) -> int:
        levels = self.levelOrder(root)
        max_sum = max(levels)
        for i in range(len(levels)):
            if levels[i] == max_sum:
                return i + 1

思路 1：复杂度分析

• 时间复杂度：$O(n)$。其中 $n$ 是二叉树的节点数目。
• 空间复杂度：$O(n)$。