1261. 在受污染的二叉树中查找元素

• 标签：树、深度优先搜索、广度优先搜索、设计、哈希表、二叉树
• 难度：中等

题目链接

• 1261. 在受污染的二叉树中查找元素 - 力扣

题目大意

描述：给出一满足下属规则的二叉树的根节点 $root$：

1. $root.val == 0$。
2. 如果 $node.val == x$ 且 $node.left \ne None$，那么 $node.left.val == 2 \times x + 1$。
3. 如果 $node.val == x$ 且 $node.right \ne None$，那么 $node.left.val == 2 \times x + 2$​。

现在这个二叉树受到「污染」，所有的 $node.val$ 都变成了 $-1$。

要求：请你先还原二叉树，然后实现 FindElements 类：

• FindElements(TreeNode* root) 用受污染的二叉树初始化对象，你需要先把它还原。
• bool find(int target) 判断目标值 $target$ 是否存在于还原后的二叉树中并返回结果。

说明：

• $node.val == -1$
• 二叉树的高度不超过 $20$。
• 节点的总数在 $[1, 10^4]$ 之间。
• 调用 find() 的总次数在 $[1, 10^4]$ 之间。
• $0 \le target \le 10^6$。

示例：

• 示例 1：

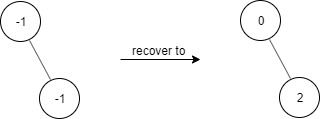
输入：
["FindElements","find","find"]
[[[-1,null,-1]],[1],[2]]
输出：
[null,false,true]
解释：
FindElements findElements = new FindElements([-1,null,-1]); 
findElements.find(1); // return False 
findElements.find(2); // return True 

• 示例 2：

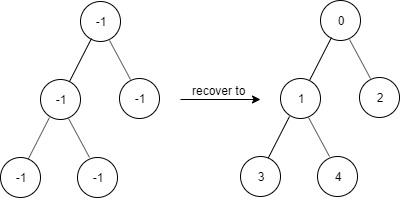
输入：
["FindElements","find","find","find"]
[[[-1,-1,-1,-1,-1]],[1],[3],[5]]
输出：
[null,true,true,false]
解释：
FindElements findElements = new FindElements([-1,-1,-1,-1,-1]);
findElements.find(1); // return True
findElements.find(3); // return True
findElements.find(5); // return False

解题思路

思路 1：哈希表 + 深度优先搜索

1. 从根节点开始进行还原。
2. 然后使用深度优先搜索的方式，依次递归还原左右两个孩子节点。
3. 递归还原的同时，将还原之后的所有节点值，存入集合 $val\underline{}set$ 中。

这样就可以在 $O(1)$ 的时间复杂度内判断目标值 $target$ 是否在还原后的二叉树中了。

思路 1：代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class FindElements:

    def __init__(self, root: Optional[TreeNode]):
        self.val_set = set()
        def dfs(node, val):
            if not node:
                return
            self.val_set.add(val)
            dfs(node.left, val * 2 + 1)
            dfs(node.right, val * 2 + 2)
        
        dfs(root, 0)


    def find(self, target: int) -> bool:
        return target in self.val_set



# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)

思路 1：复杂度分析

• 时间复杂度：还原二叉树：$O(n)$，其中 $n$ 为二叉树中的节点个数。查找目标值：$O(1)$。
• 空间复杂度：$O(n)$。