1266. 访问所有点的最小时间

ITCharge大约 3 分钟

1266. 访问所有点的最小时间

标签：几何、数组、数学
难度：简单

题目链接

1266. 访问所有点的最小时间 - 力扣

题目大意

描述：给定 $n$ 个点的整数坐标数组 $points$ 。其中 $points[i] = [xi, yi]$ ，表示第 $i$ 个点坐标为 $(xi, yi)$ 。可以按照以下规则在平面上移动：

每一秒内，可以：
1. 沿着水平方向移动一个单位长度。
2. 沿着竖直方向移动一个单位长度。
3. 沿着对角线移动 $\sqrt 2$ 个单位长度（可看做在一秒内沿着水平方向和竖直方向各移动一个单位长度）。
必须按照坐标数组 $points$ 中的顺序来访问这些点。
在访问某个点时，可以经过该点后面出现的点，但经过的那些点不算作有效访问。

要求：计算出访问这些点需要的最小时间（以秒为单位）。

说明：

$points.length == n$ 。
$1 \le n \le 100$ 。
$points[i].length == 2$ 。
$-1000 \le points[i][0], points[i][1] \le 1000$ 。

示例：

示例 1：

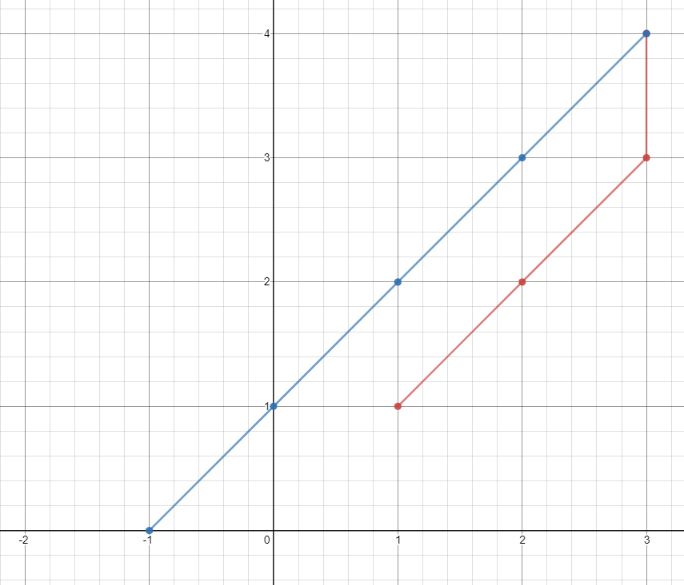
输入：points = [[1,1],[3,4],[-1,0]]
输出：7
解释：一条最佳的访问路径是： [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]   
从 [1,1] 到 [3,4] 需要 3 秒 
从 [3,4] 到 [-1,0] 需要 4 秒
一共需要 7 秒

输入：points = [[3,2],[-2,2]]
输出：5

解题思路

思路 1：数学

根据题意，每一秒可以沿着水平方向移动一个单位长度、或者沿着竖直方向移动一个单位长度、或者沿着对角线移动 $\sqrt 2$ 个单位长度。而沿着对角线移动 $\sqrt 2$ 个单位长度可以看做是先沿着水平方向移动一个单位长度，又沿着竖直方向移动一个单位长度，算是一秒走了两步距离。

现在假设从 A 点（坐标为 $(x1, y1)$ ）移动到 B 点（坐标为 $(x2, y2)$ ）。

那么从 A 点移动到 B 点如果要想得到最小时间，我们应该计算出沿着水平方向走的距离为 $dx = |x2 - x1|$ ，沿着竖直方向走的距离为 $dy = |y2 - y1|$ 。

然后比较沿着水平方向的移动距离和沿着竖直方向的移动距离。

如果 $dx > dy$ ，则我们可以先沿着对角线移动 $dy$ 次，再水平移动 $dx - dy$ 次，总共 $dx$ 次。
如果 $dx == dy$ ，则我们可以直接沿着对角线移动 $dx$ 次，总共 $dx$ 次。
如果 $dx < dy$ ，则我们可以先沿着对角线移动 $dx$ 次，再水平移动 $dy - dx$ 次，，总共 $dy$ 次。

根据上面观察可以发现：最小时间取决于「走的步数较多的那个方向所走的步数」，即 $max(dx, dy)$ 。

根据题目要求，需要按照坐标数组 $points$ 中的顺序来访问这些点，则我们需要按顺序遍历整个数组，计算出相邻点之间的 $max(dx, dy)$ ，将其累加到答案中。

最后将答案输出即可。

思路 1：代码

class Solution:
    def minTimeToVisitAllPoints(self, points: List[List[int]]) -> int:
        ans = 0
        x1, y1 = points[0]
        for point in points:
            x2, y2 = point
            ans += max(abs(x2 - x1), abs(y2 - y1))
            x1, y1 = point
        
        return ans

思路 1：复杂度分析

时间复杂度： $O(n)$ 。
空间复杂度： $O(1)$ 。