1349. 参加考试的最大学生数

• 标签：位运算、数组、动态规划、状态压缩、矩阵
• 难度：困难

题目链接

• 1349. 参加考试的最大学生数 - 力扣

题目大意

描述：给定一个 $m \times n$ 大小的矩阵 $seats$ 表示教室中的座位分布，其中如果座位是坏的（不可用），就用 '#' 表示，如果座位是好的，就用 '.' 表示。

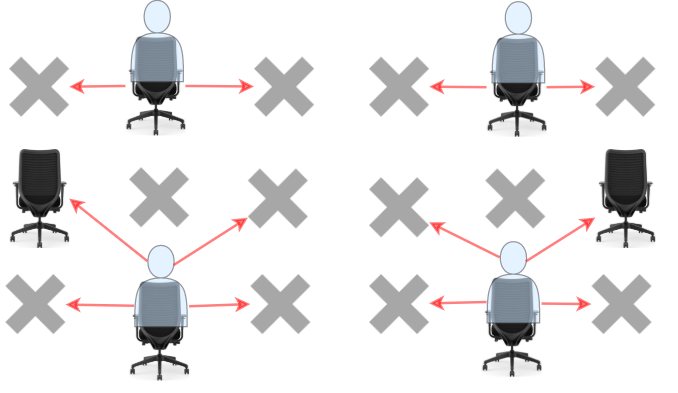
学生可以看到左侧、右侧、左上方、右上方这四个方向上紧邻他的学生答卷，但是看不到直接坐在他前面或者后面的学生答卷。

要求：计算并返回该考场可以容纳的一期参加考试且无法作弊的最大学生人数。

说明：

• 学生必须坐在状况良好的座位上。
• $seats$ 只包含字符 '.' 和 '#'。
• $m == seats.length$。
• $n == seats[i].length$。
• $1 \le m \le 8$。
• $1 \le n \le 8$。

示例：

• 示例 1：

输入：seats = [["#",".","#","#",".","#"],
              [".","#","#","#","#","."],
              ["#",".","#","#",".","#"]]
输出：4
解释：教师可以让 4 个学生坐在可用的座位上，这样他们就无法在考试中作弊。

• 示例 2：

输入：seats = [[".","#"],
              ["#","#"],
              ["#","."],
              ["#","#"],
              [".","#"]]
输出：3
解释：让所有学生坐在可用的座位上。

解题思路

思路 1：状态压缩 DP

题目中给定的 $m$、$n$ 范围为 $1 \le m, n \le 8$，每一排最多有 $8$ 个座位，那么我们可以使用一个 $8$ 位长度的二进制数来表示当前排座位的选择情况（也就是「状态压缩」的方式）。

同时从题目中可以看出，当前排的座位与当前行左侧、右侧座位有关，并且也与上一排中左上方、右上方的座位有关，则我们可以使用一个二维数组来表示状态。其中第一维度为排数，第二维度为当前排的座位选择情况。

具体做法如下：

1. 划分阶段

按照排数、当前排的座位选择情况进行阶段划分。

2. 定义状态

定义状态 $dp[i][state]$ 表示为：前 $i$ 排，并且最后一排座位选择状态为 $state$ 时，可以参加考试的最大学生数。

3. 状态转移方程

因为学生可以看到左侧、右侧、左上方、右上方这四个方向上紧邻他的学生答卷，所以对于当前排的某个座位来说，其左侧、右侧、左上方、右上方都不应有人坐。我们可以根据当前排的座位选取状态 $cur\underline{}state$，并通过枚举的方式，找出符合要求的上一排座位选取状态 $pre\underline{}state$，并计算出当前排座位选择个数，即 $f(cur\underline{}state)$，则状态转移方程为：

$dp[i][state] = \max \lbrace dp[i - 1][pre\underline{}state]\rbrace + f(state) $

因为所给座位中还有坏座位（不可用）的情况，我们可以使用一个 $8$ 位的二进制数 $bad\underline{}seat$ 来表示当前排的坏座位情况，如果 $cur\underline{}state \text{ \& } bad\underline{}seat == 1$，则说明当前状态下，选择了坏椅子，则可直接跳过这种状态。

我们还可以通过 $cur\underline{}state \text{ \& } (cur\underline{}state \text{ <}\text{< } 1)$ 和 $cur\underline{}state \& (cur\underline{}state \text{ >}\text{> } 1)$ 来判断当前排选择状态下，左右相邻座位上是否有人，如果有人，则可直接跳过这种状态。

同理，我们还可以通过 $cur\underline{}state \text{ \& } (pre\underline{}state \text{ <}\text{< } 1)$ 和 $cur\underline{}state \text{ \& } (pre\underline{}state \text{ >}\text{> } 1)$ 来判断当前排选择状态下，上一行左上、右上相邻座位上是否有人，如果有人，则可直接跳过这种状态。

4. 初始条件

• 默认情况下，前 $0$ 排所有选择状态下，可以参加考试的最大学生数为 $0$。

5. 最终结果

根据我们之前定义的状态，$dp[i][state]$ 表示为：前 $i$ 排，并且最后一排座位选择状态为 $state$ 时，可以参加考试的最大学生数。 所以最终结果为最后一排 $dp[rows]$ 中的最大值。

思路 1：代码

class Solution:
    def maxStudents(self, seats: List[List[str]]) -> int:
        rows, cols = len(seats), len(seats[0])
        states = 1 << cols
        dp = [[0 for _ in range(states)] for _ in range(rows + 1)]

        for i in range(1, rows + 1):                    # 模拟 1 ~ rows 排分配座位
            bad_seat = 0                                # 当前排的坏座位情况
            for j in range(cols):
                if seats[i - 1][j] == '#':              # 记录坏座位情况
                    bad_seat |= 1 << j

            for cur_state in range(states):             # 枚举当前排的座位选取状态
                if cur_state & bad_seat:                # 当前排的座位选择了换座位，跳过
                    continue
                if cur_state & (cur_state << 1):        # 当前排左侧座位有人，跳过
                    continue
                if cur_state & (cur_state >> 1):        # 当前排右侧座位有人，跳过
                    continue

                count = bin(cur_state).count('1')       # 计算当前排最多可以坐多少人
                for pre_state in range(states):         # 枚举前一排情况
                    if cur_state & (pre_state << 1):    # 左上座位有人，跳过
                        continue
                    if cur_state & (pre_state >> 1):    # 右上座位有人，跳过
                        continue
                    # dp[i][cur_state] 取自上一排分配情况为 pre_state 的最大值 + 当前排最多可以坐的人数
                    dp[i][cur_state] = max(dp[i][cur_state], dp[i - 1][pre_state] + count)

        return max(dp[rows])

思路 1：复杂度分析

• 时间复杂度：$O(m \times 2^{2n})$，其中 $m$、$n$ 分别为所给矩阵的行数、列数。
• 空间复杂度：$O(m \times 2^n)$。