1319. 连通网络的操作次数

• 标签：深度优先搜索、广度优先搜索、并查集、图
• 难度：中等

题目链接

• 1319. 连通网络的操作次数 - 力扣

题目大意

描述：$n$ 台计算机通过网线连接成一个网络，计算机的编号从 $0$ 到 $n - 1$。线缆用 $comnnections$ 表示，其中 $connections[i] = [a, b]$ 表示连接了计算机 $a$ 和 $b$。

给定这个计算机网络的初始布线 $connections$，可以拔除任意两台直接相连的计算机之间的网线，并用这根网线连接任意一对未直接连接的计算机。

要求：计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 $-1$。

说明：

• $1 \le n \le 10^5$。
• $1 \le connections.length \le min( \frac{n \times (n-1)}{2}, 10^5)$。
• $connections[i].length == 2$。
• $0 \le connections[i][0], connections[i][1] < n$。
• $connections[i][0] != connections[i][1]$。
• 没有重复的连接。
• 两台计算机不会通过多条线缆连接。

示例：

• 示例 1：

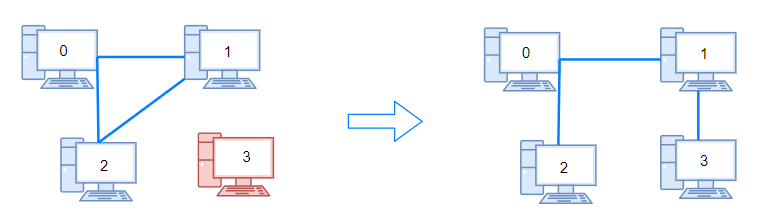
输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

• 示例 2：

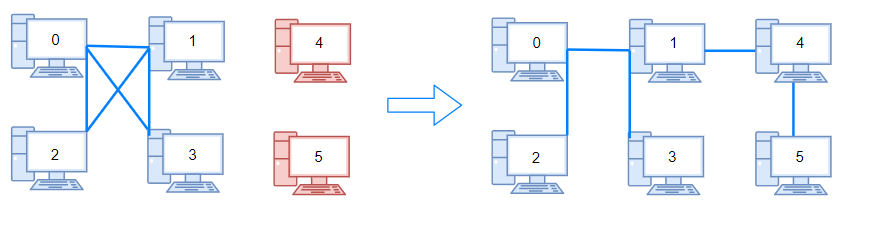
输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出：2

解题思路

思路 1：并查集

$n$ 台计算机至少需要 $n - 1$ 根线才能进行连接，如果网线的数量少于 $n - 1$，那么就不可能将其连接。接下来计算最少操作次数。

把 $n$ 台计算机看做是 $n$ 个节点，每条网线看做是一条无向边。维护两个变量：多余电线数 $removeCount$、需要电线数 $needConnectCount$。初始 $removeCount = 1, needConnectCount = n - 1$。

遍历网线数组，将相连的节点 $a$ 和 $b$ 利用并查集加入到一个集合中（调用 union 操作）。

• 如果 $a$ 和 $b$ 已经在同一个集合中，说明该连接线多余，多余电线数加 $1$。
• 如果 $a$ 和 $b$ 不在一个集合中，则将其合并，则 $a$ 和 $b$ 之间不再需要用额外的电线连接了，所以需要电线数减 $1$。

最后，判断多余的电线数是否满足需要电线数，不满足返回 $-1$，如果满足，则返回需要电线数。

思路 1：代码

class UnionFind:

    def __init__(self, n):
        self.parent = [i for i in range(n)]

    def find(self, x):
        while x != self.parent[x]:
            self.parent[x] = self.parent[self.parent[x]]
            x = self.parent[x]
        return x

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False
        self.parent[root_x] = root_y
        return True

    def is_connected(self, x, y):
        return self.find(x) == self.find(y)

class Solution:
    def makeConnected(self, n: int, connections: List[List[int]]) -> int:
        union_find = UnionFind(n)
        removeCount = 0
        needConnectCount = n - 1
        for connection in connections:
            if union_find.union(connection[0], connection[1]):
                needConnectCount -= 1
            else:
                removeCount += 1

        if removeCount < needConnectCount:
            return -1
        return needConnectCount

思路 1：复杂度分析

• 时间复杂度：$O(m \times \alpha(n))$，其中 $m$ 是数组 $connections$ 的长度，$\alpha$ 是反 Ackerman 函数。
• 空间复杂度：$O(n)$。