1496. 判断路径是否相交

• 标签：哈希表、字符串
• 难度：简单

题目链接

• 1496. 判断路径是否相交 - 力扣

题目大意

描述：给定一个字符串 $path$，其中 $path[i]$ 的值可以是 'N'、'S'、'E' 或者 'W'，分别表示向北、向南、向东、向西移动一个单位。

你从二维平面上的原点 $(0, 0)$ 处开始出发，按 $path$ 所指示的路径行走。

要求：如果路径在任何位置上与自身相交，也就是走到之前已经走过的位置，请返回 $True$；否则，返回 $False$。

说明：

• $1 \le path.length \le 10^4$。
• $path[i]$ 为 'N'、'S'、'E' 或 'W'。

示例：

• 示例 1：

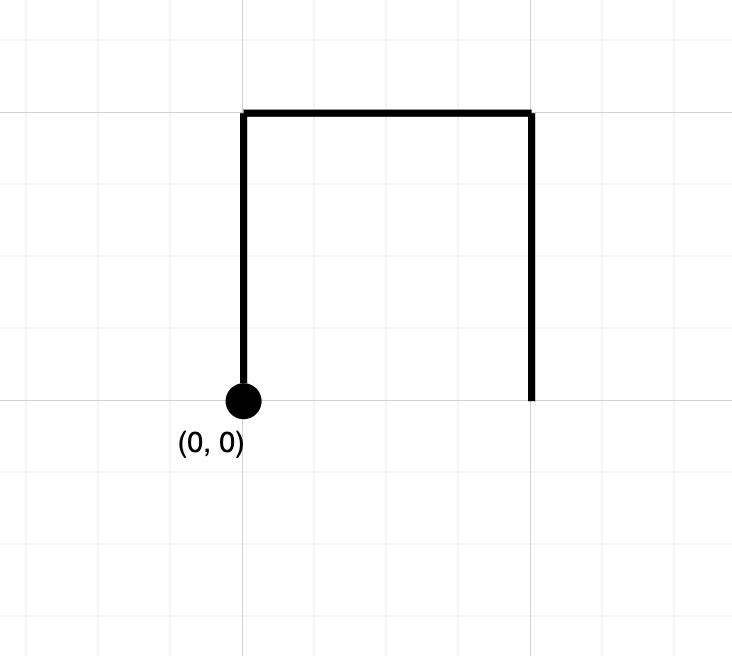
输入：path = "NES"
输出：false 
解释：该路径没有在任何位置相交。

• 示例 2：

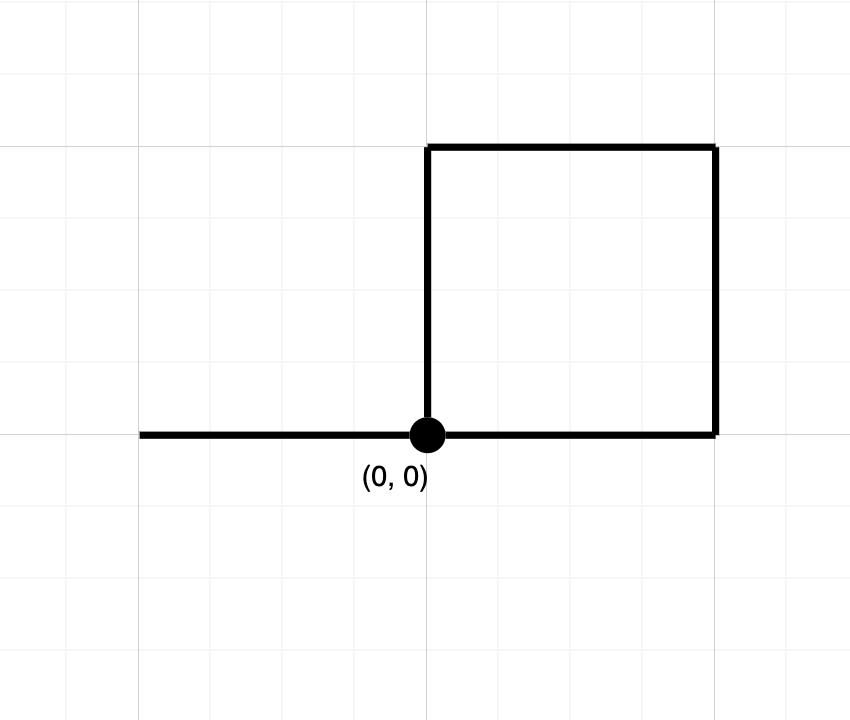
输入：path = "NESWW"
输出：true
解释：该路径经过原点两次。

解题思路

思路 1：哈希表 + 模拟

1. 使用哈希表将 'N'、'S'、'E'、'W' 对应横纵坐标轴上的改变表示出来。
2. 使用集合 $visited$ 存储走过的坐标元组。
3. 遍历 $path$，按照 $path$ 所指示的路径模拟行走，并将所走过的坐标使用 $visited$ 存储起来。
4. 如果在 $visited$ 遇到已经走过的坐标，则返回 $True$。
5. 如果遍历完仍未发现已经走过的坐标，则返回 $False$。

思路 1：代码

class Solution:
    def isPathCrossing(self, path: str) -> bool:
        directions = {
            "N" : (-1, 0),
            "S" : (1, 0),
            "W" : (0, -1),
            "E" : (0, 1),
        }

        x, y = 0, 0
        
        visited = set()
        visited.add((x, y))
        
        for ch in path:
            x += directions[ch][0]
            y += directions[ch][1]
            if (x, y) in visited:
                return True
            visited.add((x, y))
        
        return False

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 为数组 $path$ 的长度。
• 空间复杂度：$O(n)$。