1595. 连通两组点的最小成本

• 标签：位运算、数组、动态规划、状态压缩、矩阵
• 难度：困难

题目链接

• 1595. 连通两组点的最小成本 - 力扣

题目大意

描述：有两组点，其中一组中有 $size_1$ 个点，第二组中有 $size_2$ 个点，且 $size_1 \ge size_2$。现在给定一个大小为 $size_1 \times size_2$ 的二维数组 $cost$ 用于表示两组点任意两点之间的链接成本。其中 $cost[i][j]$ 表示第一组中第 $i$ 个点与第二组中第 $j$ 个点的链接成本。

如果两个组中每个点都与另一个组中的一个或多个点连接，则称这两组点是连通的。

要求：返回连通两组点所需的最小成本。

说明：

• $size_1 == cost.length$。
• $size_2 == cost[i].length$。
• $1 \le size_1, size_2 \le 12$。
• $size_1 \ge size_2$。
• $0 \le cost[i][j] \le 100$。

示例：

• 示例 1：

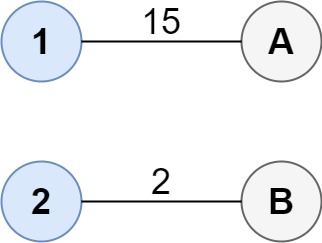
输入：cost = [[15, 96], [36, 2]]
输出：17
解释：连通两组点的最佳方法是：
1--A
2--B
总成本为 17。

• 示例 2：

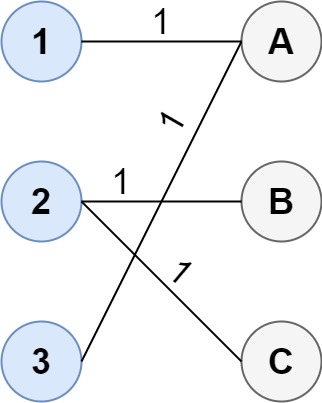
输入：cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
输出：4
解释：连通两组点的最佳方法是：
1--A
2--B
2--C
3--A
最小成本为 4。
请注意，虽然有多个点连接到第一组中的点 2 和第二组中的点 A ，但由于题目并不限制连接点的数目，所以只需要关心最低总成本。

解题思路

思路 1：状压 DP

思路 1：代码

class Solution:
    def connectTwoGroups(self, cost: List[List[int]]) -> int:
        m, n = len(cost), len(cost[0])
        states = 1 << n
        dp = [[float('inf') for _ in range(states)] for _ in range(m + 1)]
        dp[0][0] = 0
        for i in range(1, m + 1):
            for state in range(states):
                for j in range(n):
                    dp[i][state | (1 << j)] = min(dp[i][state | (1 << j)], dp[i - 1][state] + cost[i - 1][j], dp[i][state] + cost[i - 1][j])

        return dp[m][states - 1]

思路 1：复杂度分析

• 时间复杂度：
• 空间复杂度：