1582. 二进制矩阵中的特殊位置

• 标签：数组、矩阵
• 难度：简单

题目链接

• 1582. 二进制矩阵中的特殊位置 - 力扣

题目大意

描述：给定一个 $m \times n$ 的二进制矩阵 $mat$。

要求：返回矩阵 $mat$ 中特殊位置的数量。

说明：

• 特殊位置：如果位置 $(i, j)$ 满足 $mat[i][j] == 1$ 并且行 $i$ 与列 $j$ 中的所有其他元素都是 $0$（行和列的下标从 $0$ 开始计数），那么它被称为特殊位置。
• $m == mat.length$。
• $n == mat[i].length$。
• $1 \le m, n \le 100$。
• $mat[i][j]$ 是 $0$ 或 $1$。

示例：

• 示例 1：

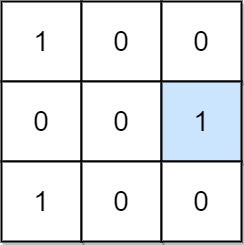
输入：mat = [[1,0,0],[0,0,1],[1,0,0]]
输出：1
解释：位置 (1, 2) 是一个特殊位置，因为 mat[1][2] == 1 且第 1 行和第 2 列的其他所有元素都是 0。

• 示例 2：

img

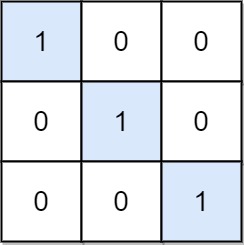
输入：mat = [[1,0,0],[0,1,0],[0,0,1]]
输出：3
解释：位置 (0, 0)，(1, 1) 和 (2, 2) 都是特殊位置。

解题思路

思路 1：模拟

1. 按照行、列遍历二位数组 $mat$。
2. 使用数组 $row\underline{}cnts$、$col\underline{}cnts$ 分别记录每行和每列所含 $1$ 的个数。
3. 再次按照行、列遍历二维数组 $mat$。
4. 统计满足 $mat[row][col] == 1$ 并且 $row\underline{}cnts[row] == col\underline{}cnts[col] == 1$ 的位置个数。
5. 返回答案。

思路 1：代码

class Solution:
    def numSpecial(self, mat: List[List[int]]) -> int:
        rows, cols = len(mat), len(mat[0])
        row_cnts = [0 for _ in range(rows)]
        col_cnts = [0 for _ in range(cols)]

        for row in range(rows):
            for col in range(cols):
                row_cnts[row] += mat[row][col]
                col_cnts[col] += mat[row][col]

        ans = 0
        for row in range(rows):
            for col in range(cols):
                if mat[row][col] == 1 and row_cnts[row] == 1 and col_cnts[col] == 1:
                    ans += 1
        
        return ans

思路 1：复杂度分析

• 时间复杂度：$O(m \times n)$，其中 $m$、$n$ 分别为数组 $mat$ 的行数和列数。
• 空间复杂度：$O(m + n)$。