1791. 找出星型图的中心节点

• 标签：图
• 难度：简单

题目链接

• 1791. 找出星型图的中心节点 - 力扣

题目大意

描述：有一个无向的行型图，由 $n$ 个编号 $1 \sim n$ 的节点组成。星型图有一个中心节点，并且恰好有 $n - 1$ 条边将中心节点与其他每个节点连接起来。

给定一个二维整数数组 $edges$，其中 $edges[i] = [u_i, v_i]$ 表示节点 $u_i$ 与节点 $v_i$ 之间存在一条边。

要求：找出并返回该星型图的中心节点。

说明：

• $3 \le n \le 10^5$。
• $edges.length == n - 1$。
• $edges[i].length == 2$。
• $1 \le ui, vi \le n$。
• $ui \ne vi$。
• 题目数据给出的 $edges$ 表示一个有效的星型图。

示例：

• 示例 1：

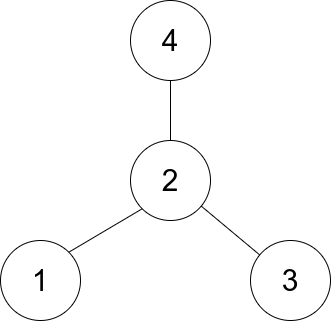
输入：edges = [[1,2],[2,3],[4,2]]
输出：2
解释：如上图所示，节点 2 与其他每个节点都相连，所以节点 2 是中心节点。

• 示例 2：

输入：edges = [[1,2],[5,1],[1,3],[1,4]]
输出：1

解题思路

思路 1：求度数

根据题意可知：中心节点恰好有 $n - 1$ 条边将中心节点与其他每个节点连接起来，那么中心节点的度数一定为 $n - 1$。则我们可以遍历边集数组 $edges$，统计出每个节点 $u$ 的度数 $degrees[u]$。最后返回度数为 $n - 1$ 的节点编号。

思路 1：代码

class Solution:
    def findCenter(self, edges: List[List[int]]) -> int:
        n = len(edges) + 1
        degrees = collections.Counter()

        for u, v in edges:
            degrees[u] += 1
            degrees[v] += 1

        for i in range(1, n + 1):
            if degrees[i] == n - 1:
                return i
        return -1

思路 1：复杂度分析

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(n)$。