2050. 并行课程 III

ITCharge大约 3 分钟

2050. 并行课程 III

标签：图、拓扑排序、数组、动态规划
难度：困难

题目链接

2050. 并行课程 III - 力扣

题目大意

描述：给定一个整数 $n$ ，表示有 $n$ 节课，课程编号为 $1 \sim n$ 。

再给定一个二维整数数组 $relations$ ，其中 $relations[j] = [prevCourse_j, nextCourse_j]$ ，表示课程 $prevCourse_j$ 必须在课程 $nextCourse_j$ 之前完成（先修课的关系）。

再给定一个下标从 $0$ 开始的整数数组 $time$ ，其中 $time[i]$ 表示完成第 $(i + 1)$ 门课程需要花费的月份数。

现在根据以下规则计算完成所有课程所需要的最少月份数：

如果一门课的所有先修课都已经完成，则可以在任意时间开始这门课程。
可以同时上任意门课程。

要求：返回完成所有课程所需要的最少月份数。

说明：

$1 \le n \le 5 * 10^4$ 。
$0 \le relations.length \le min(n * (n - 1) / 2, 5 \times 10^4)$ 。
$relations[j].length == 2$ 。
$1 \le prevCourse_j, nextCourse_j \le n$ 。
$prevCourse_j != nextCourse_j$ 。
所有的先修课程对 $[prevCourse_j, nextCourse_j]$ 都是互不相同的。
$time.length == n$ 。
$1 \le time[i] \le 10^4$ 。
先修课程图是一个有向无环图。

示例：

示例 1：

输入：n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出：8
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月，课程 2 花费 2 个月。
所以，最早开始课程 3 的时间是月份 3 ，完成所有课程所需时间为 3 + 5 = 8 个月。

示例 2：

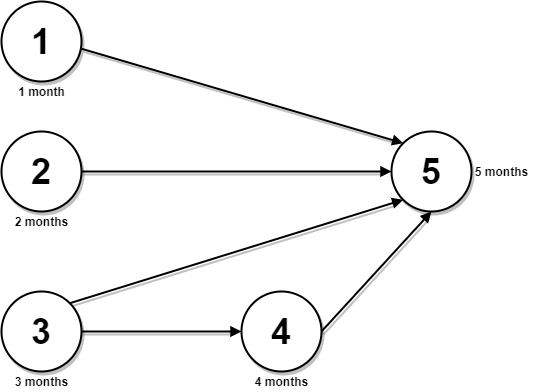
输入：n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出：12
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ，2 和 3 。
在月份 1，2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始，也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1，2，3 和 4 之后开始，也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。

解题思路

思路 1：拓扑排序 + 动态规划

使用邻接表 $graph$ 存放课程关系图，并统计每门课程节点的入度，存入入度列表 $indegrees$ 。定义 $dp[i]$ 为完成第 $i$ 门课程所需要的最少月份数。使用 $ans$ 表示完成所有课程所需要的最少月份数。
借助队列 $queue$ ，将所有入度为 $0$ 的节点入队。
将队列中入度为 $0$ $0$ 的节点依次取出。对于取出的每个节点 $u$ $u$ ：
1. 遍历该节点的相邻节点 $v$ ，更新相邻节点 $v$ 所需要的最少月份数，即： $dp[v] = max(dp[v], dp[u] + time[v - 1])$ 。
2. 更新完成所有课程所需要的最少月份数 $ans$ ，即： $ans = max(ans, dp[v])$ 。
3. 相邻节点 $v$ 的入度减 $1$ ，如果入度减 $1$ 后的节点入度为 0，则将其加入队列 $queue$ 。
重复 $3$ 的步骤，直到队列中没有节点。
最后返回 $ans$ 。

思路 1：代码

class Solution:
    def minimumTime(self, n: int, relations: List[List[int]], time: List[int]) -> int:
        graph = [[] for _ in range(n + 1)]
        indegrees = [0 for _ in range(n + 1)]

        for u, v in relations:
            graph[u].append(v)
            indegrees[v] += 1

        queue = collections.deque()
        dp = [0 for _ in range(n + 1)]

        ans = 0
        for i in range(1, n + 1):
            if indegrees[i] == 0:
                queue.append(i)
                dp[i] = time[i - 1]
                ans = max(ans, time[i - 1])

        while queue:
            u = queue.popleft()
            for v in graph[u]:
                dp[v] = max(dp[v], dp[u] + time[v - 1])
                ans = max(ans, dp[v])
                indegrees[v] -= 1
                if indegrees[v] == 0:
                    queue.append(v)

        return ans

思路 1：复杂度分析

时间复杂度： $O(m + n)$ ，其中 $m$ 为数组 $relations$ 的长度。
空间复杂度： $O(m + n)$ 。