2538. 最大价值和与最小价值和的差值

ITCharge大约 5 分钟

2538. 最大价值和与最小价值和的差值

标签：树、深度优先搜索、数组、动态规划
难度：困难

题目链接

2538. 最大价值和与最小价值和的差值 - 力扣

题目大意

描述：给定一个整数 $n$ 和一个长度为 $n - 1$ 的二维整数数组 $edges$ 用于表示一个 $n$ 个节点的无向无根图，节点编号为 $0 \sim n - 1$ 。其中 $edges[i] = [ai, bi]$ 表示树中节点 $ai$ 和 $bi$ 之间有一条边。再给定一个整数数组 $price$ ，其中 $price[i]$ 表示图中节点 $i$ 的价值。

一条路径的价值和是这条路径上所有节点的价值之和。

你可以选择树中任意一个节点作为根节点 $root$ 。选择 $root$ 为根的开销是以 $root$ 为起点的所有路径中，价值和最大的一条路径与最小的一条路径的差值。

要求：返回所有节点作为根节点的选择中，最大的开销为多少。

说明：

$1 \le n \le 10^5$ 。
$edges.length == n - 1$ 。
$0 \le ai, bi \le n - 1$ 。
$edges$ 表示一棵符合题面要求的树。
$price.length == n$ 。
$1 \le price[i] \le 10^5$ 。

示例：

示例 1：

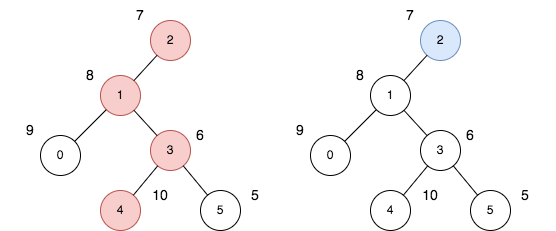
输入：n = 6, edges = [[0,1],[1,2],[1,3],[3,4],[3,5]], price = [9,8,7,6,10,5]
输出：24
解释：上图展示了以节点 2 为根的树。左图（红色的节点）是最大价值和路径，右图（蓝色的节点）是最小价值和路径。
- 第一条路径节点为 [2,1,3,4]：价值为 [7,8,6,10] ，价值和为 31 。
- 第二条路径节点为 [2] ，价值为 [7] 。
最大路径和与最小路径和的差值为 24 。24 是所有方案中的最大开销。

示例 2：

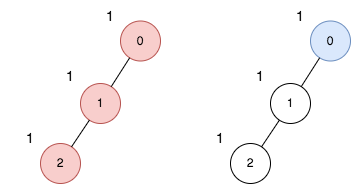
输入：n = 3, edges = [[0,1],[1,2]], price = [1,1,1]
输出：2
解释：上图展示了以节点 0 为根的树。左图（红色的节点）是最大价值和路径，右图（蓝色的节点）是最小价值和路径。
- 第一条路径包含节点 [0,1,2]：价值为 [1,1,1] ，价值和为 3 。
- 第二条路径节点为 [0] ，价值为 [1] 。
最大路径和与最小路径和的差值为 2 。2 是所有方案中的最大开销。

解题思路

思路 1：树形 DP + 深度优先搜索

因为 $price$ 数组中元素都为正数，所以价值和最小的一条路径一定为「单个节点」，也就是根节点 $root$ 本身。
因为价值和最大的路径是从根节点 $root$ 出发的价值和最大的一条路径，所以「最大的开销」等于「从根节点 $root$ 出发的价值和最大的一条路径」与「路径中一个端点值」的差值。
价值和最大的路径的两个端点中，一个端点为根节点 $root$ ，另一个节点为叶子节点。

这样问题就变为了求树中一条路径，使得路径的价值和减去其中一个端点值的权值最大。

对此我们可以使用深度优先搜索递归遍历二叉树，并在递归遍历的同时，维护一个最大开销变量 $ans$ 。

然后定义函数 def dfs(self, u, father): 计算以节点 $u$ 为根节点的子树中，带端点的最大路径和 $max\underline{\hspace{0.5em}}s1$ ，以及去掉端点的最大路径和 $max\underline{\hspace{0.5em}}s2$ ，其中 $father$ 表示节点 $u$ 的根节点，用于遍历邻接节点的过程中过滤父节点，避免重复遍历。

初始化带端点的最大路径和 $max\underline{\hspace{0.5em}}s1$ 为 $price[u]$ ，表示当前只有一个节点，初始化去掉端点的最大路径和 $max\underline{\hspace{0.5em}}s2$ 为 $0$ ，表示当前没有节点。

然后在遍历节点 $u$ 的相邻节点 $v$ 时，递归调用 $dfs(v, u)$ ，获取以节点 $v$ 为根节点的子树中，带端点的最大路径和 $s1$ ，以及去掉端点的最大路径和 $s2$ 。此时最大开销变量 $self.ans$ 有两种情况：

$u$ 的子树中带端点的最大路径和，加上 $v$ 的子树中不带端点的最大路径和，即： $max\underline{\hspace{0.5em}}s1 + s2$ 。
$u$ 的子树中去掉端点的最大路径和，加上 $v$ 的子树中带端点的最大路径和，即： $max\underline{\hspace{0.5em}}s2 + s1$ 。

此时我们更新最大开销变量 $self.ans$ ，即： $self.ans = max(self.ans, \quad max\underline{\hspace{0.5em}}s1 + s2, \quad max\underline{\hspace{0.5em}}s2 + s1)$ 。

然后更新 $u$ 的子树中带端点的最大路径和 $max\underline{\hspace{0.5em}}s1$ ，即： $max\underline{\hspace{0.5em}}s1= max(max\underline{\hspace{0.5em}}s1, \quad s1 + price[u])$ 。

再更新 $u$ 的子树中去掉端点的最大路径和 $max\underline{\hspace{0.5em}}s2$ ，即： $max\underline{\hspace{0.5em}}s2 = max(max\underline{\hspace{0.5em}}s2, \quad s2 + price[u])$ 。

最后返回带端点 $u$ 的最大路径和 $max\underline{\hspace{0.5em}}s1$ ，以及去掉端点 $u$ 的最大路径和 $。

最终，最大开销变量 $self.ans$ 即为答案。

思路 1：代码

class Solution:
    def __init__(self):
        self.ans = 0
        
    def dfs(self, graph, price, u, father):
        max_s1 = price[u]
        max_s2 = 0
        for v in graph[u]:
            if v == father:    # 过滤父节点，避免重复遍历
                continue
            s1, s2 = self.dfs(graph, price, v, u)
            self.ans = max(self.ans, max_s1 + s2, max_s2 + s1)
            max_s1 = max(max_s1, s1 + price[u])
            max_s2 = max(max_s2, s2 + price[u])
        return max_s1, max_s2

    def maxOutput(self, n: int, edges: List[List[int]], price: List[int]) -> int:
        graph = [[] for _ in range(n)]
        for u, v in edges:
            graph[u].append(v)
            graph[v].append(u)

        self.dfs(graph, price, 0, -1)
        return self.ans

思路 1：复杂度分析

时间复杂度： $O(n)$ ，其中 $n$ 为树中节点个数。
空间复杂度： $O(n)$ 。

参考链接

【题解】二维差分模板双指针树形DP 树的直径【力扣周赛 328】
【题解】[2538. 最大价值和与最小价值和的差值题解](https://github.com/doocs/leetcode/blob/main/solution/2500-2599/2538.Difference Between Maximum and Minimum Price Sum/README.md)