1.1 数组基础
1.1 数组基础
---1. 数组简介
1.1 数组定义
数组(Array):一种线性表数据结构,利用一段连续的内存空间,存储一组相同类型的数据。
简而言之,「数组」 是线性表顺序存储结构的典型代表。
以整数数组为例,其存储方式如下图所示:
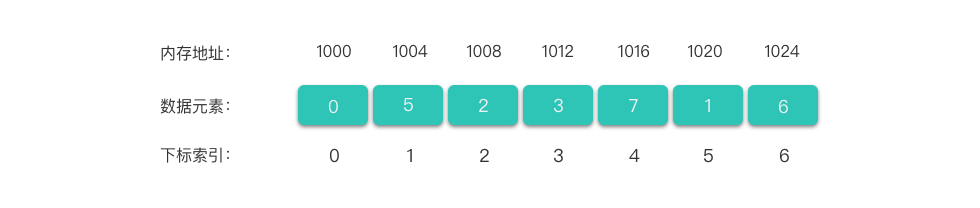
如上图,假设数组包含 个元素,每个元素都有唯一的下标索引,范围从 到 。每个下标对应一个数据元素。
可以看出,数组在计算机中本质上是一段连续的内存区域。每个元素都占用相同大小的存储单元,这些单元都有自己的内存地址,并且在物理内存中是依次排列的。
我们可以从两个角度理解数组的定义:
- 线性表:线性表是一种数据元素顺序排列、类型相同的数据结构,每个元素最多只有前驱和后继两个相邻元素。数组正是线性表的一种典型实现,此外,栈、队列、链表等也属于线性表结构。
- 连续的内存空间:线性表有「顺序存储」和「链式存储」两种方式。顺序存储结构要求内存空间连续,相邻元素在物理内存中紧挨着。数组采用的正是顺序存储结构,且所有元素类型一致。
综合这两个角度,数组可以看作是采用「顺序存储结构」实现的「线性表」。
1.2 如何随机访问数据元素
数组最显著的特点是:支持随机访问。也就是说,可以通过下标直接定位并访问任意一个元素。
那么,计算机是如何实现通过下标高效访问数组元素的呢?
实际上,数组在内存中被分配为一段连续的空间,第一个元素的地址称为 「首地址」。每个元素都有唯一的下标和对应的内存地址。计算机在访问数组元素时,会利用下标通过 「寻址公式」 快速计算出目标元素的内存地址,从而实现高效访问。
寻址公式为:下标 的元素地址 = 首地址 + × 单个元素占用的字节数
1.3 多维数组
前面介绍的是只有一个维度的数组,称为一维数组,其每个数据元素都通过单一的下标进行访问。但在实际应用中,许多数据具有二维或多维结构,一维数组已无法满足需求,因此引入了多维数组的概念。
以二维数组为例,其结构如下图所示:
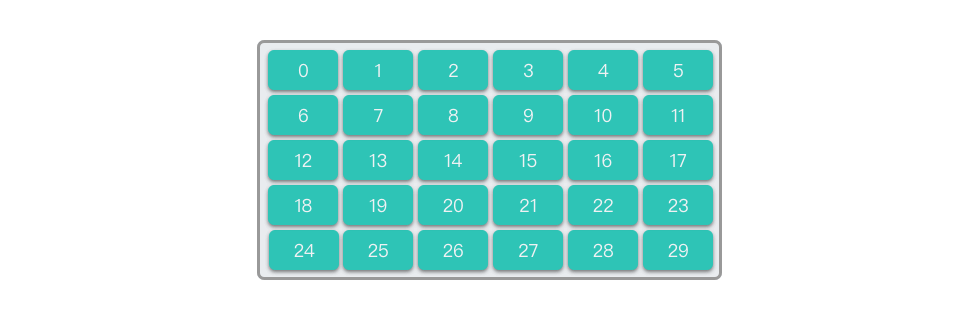
二维数组由 行 列的数据元素组成,本质上可以理解为「数组的数组」,即每个元素本身也是一个数组。第一维表示行,第二维表示列。在内存中,二维数组通常采用行优先或列优先的存储方式。
二维数组常被视为矩阵,可以用于处理如矩阵转置、矩阵加法、矩阵乘法等相关问题。
1.4 不同编程语言中数组的实现
在不同的编程语言中,数组的数据结构实现存在一定差异。
C / C++ 语言中的数组实现最贴合数据结构中对数组的定义:它们使用一块连续的内存空间来存储相同类型的数据元素。无论是基本数据类型,还是结构体、对象,在数组中都以连续方式排列。例如:
int arr[3][4] = {{0, 1, 2, 3}, {4, 5, 6, 7}, {8, 9, 10, 11}};Java 中的数组同样用于存储相同类型的数据,并且在底层实现中也是连续存储的。但在多维数组的情况下,Java 允许创建不规则数组(jagged array),即每个嵌套数组的长度可以不同。例如:
int[][] arr = new int[3][];
arr[0] = new int[]{1, 2, 3};
arr[1] = new int[]{4, 5};
arr[2] = new int[]{6, 7, 8, 9};在原生 Python 中,并不存在严格意义上的「数组」这一数据结构,而是提供了一种名为「列表(list)」的容器类型,功能类似于 Java 中的 ArrayList。我们通常将列表作为 Python 中的数组来使用。与传统数组不同,Python 的列表不仅可以存储不同类型的数据元素,长度也可以动态变化,并且支持丰富的内置方法。例如:
arr = ['python', 'java', ['asp', 'php'], 'c']2. 数组的基本操作
数组的基本操作主要包括增、删、改、查四类,下面我们分别介绍数组在这四种操作下的实现方式。
2.1 访问元素
访问数组中第 个元素:
- 首先检查下标 是否在合法范围内,即 ,超出该范围属于非法访问。
- 如果下标合法,则可直接通过下标获取对应元素的值。
- 如果下标不合法,则抛出异常或返回特殊值。
# 从数组 nums 中读取下标为 i 的数据元素值
def get_element(nums: list[int], index: int):
"""获取数组中指定下标的元素值"""
if 0 <= index < len(nums):
return nums[index]
else:
raise IndexError(f"数组下标 {index} 超出范围 [0, {len(nums)-1}]")
# 示例用法
arr = [0, 5, 2, 3, 7, 1, 6]
print(get_element(arr, 3)) # 输出: 3「访问数组元素」的操作不依赖于数组中元素个数,因此,「访问数组元素」的时间复杂度为 。
2.2 查找元素
查找数组中元素值为 的位置:
- 遍历数组,将目标值 与每个元素进行比较。
- 找到匹配元素时返回其下标。
- 遍历完未找到时返回特殊值(如 )。
def find_element(nums: list[int], val: int):
"""查找数组中元素值为 val 的位置"""
for i in range(len(nums)):
if nums[i] == val:
return i
return -1
# 示例用法
arr = [0, 5, 2, 3, 7, 1, 6]
print(find_element(arr, 5)) # 输出: 1
print(find_element(arr, 9)) # 输出: -1 (未找到)当数组无序时,查找元素只能通过将 与数组中的每个元素依次比较,这种方式称为线性查找。由于需要遍历整个数组,线性查找的时间复杂度为 。
2.3 插入元素
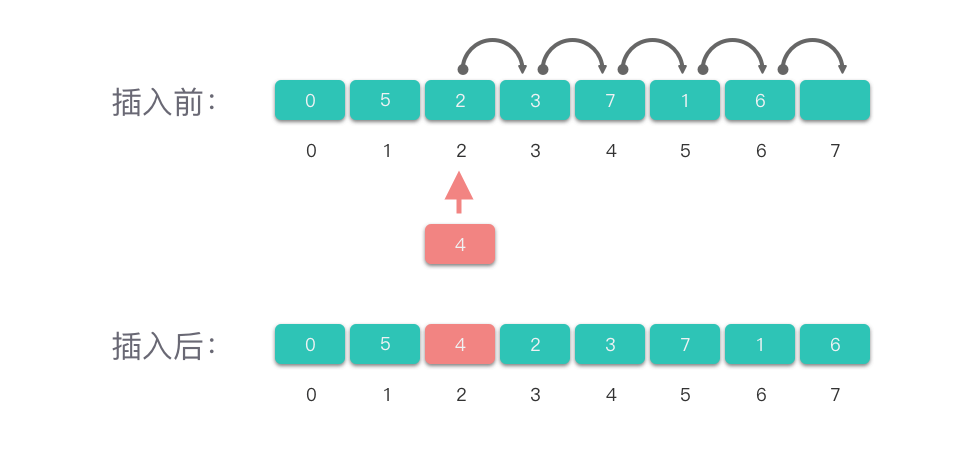
在数组第 个位置插入值 :
- 检查 是否在 范围内。
- 扩展数组长度,为新元素腾出空间。
- 将 及其后的元素整体向后移动一位。
- 在 位置插入 。
def insert_element(nums: list[int], index: int, val: int):
"""在指定位置插入元素"""
# 检查 index 是否在有效范围内
if 0 <= index <= len(nums):
# 扩展数组长度,在末尾添加一个占位元素
nums.append(0)
# 将 index 及其后的元素整体向后移动一位
for i in range(len(nums) - 1, index, -1):
nums[i] = nums[i - 1]
# 在 index 位置插入 val
nums[index] = val
return True
else:
# 索引不在范围内,返回错误
return False
# 示例用法
arr = [0, 5, 2, 3, 7, 1, 6]
result = insert_element(arr, 2, 4)
print(f"插入结果: {result}") # 输出: 插入结果: True
print(f"插入后数组: {arr}") # 输出: [0, 5, 4, 2, 3, 7, 1, 6]「在数组中间位置插入元素」的操作中,由于移动元素的操作次数跟元素个数有关,因此,「在数组中间位置插入元素」的最坏和平均时间复杂度都是 。
2.4 改变元素
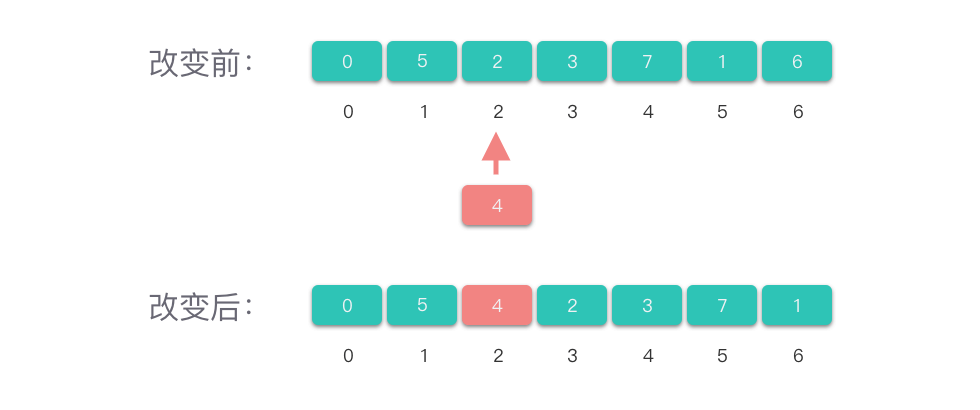
将数组中第 个元素值改为 :
- 检查 是否在 范围内。
- 将第 个元素值赋值为 。
def change_element(nums: list[int], index: int, val: int):
"""修改数组中指定位置的元素值"""
if 0 <= index < len(nums):
nums[index] = val
return True
else:
return False # 索引超出范围
# 示例用法
arr = [0, 5, 2, 3, 7, 1, 6]
result = change_element(arr, 2, 4)
print(f"修改结果: {result}") # 输出: 修改结果: True
print(f"修改后数组: {arr}") # 输出: [0, 5, 4, 3, 7, 1, 6]「改变元素」操作与访问元素类似,都是通过下标直接定位,无需遍历数组,操作时间与数组长度无关,因此其时间复杂度为 。
2.5 删除元素
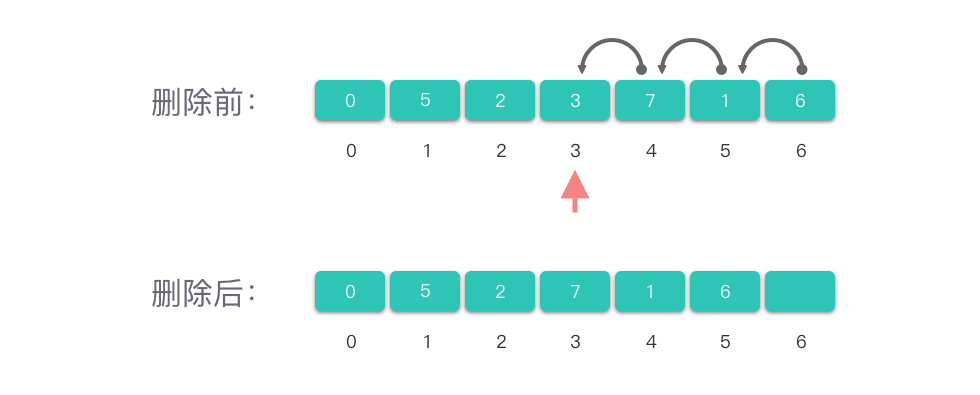
删除数组中第 个位置的元素:
- 检查下标 是否在合法范围内,即 。
- 将 位置及其后的元素整体向前移动一位。
- 删除最后一个元素(或更新数组长度)。
def delete_element(nums: list[int], index: int):
"""删除数组中指定位置的元素"""
if 0 <= index < len(nums):
# 将 index 后的元素整体向前移动一位
for i in range(index, len(nums) - 1):
nums[i] = nums[i + 1]
# 删除最后一个元素(或更新数组长度)
nums.pop()
return True
else:
return False # 索引超出范围
# 示例用法
arr = [0, 5, 2, 3, 7, 1, 6]
result = delete_element(arr, 2)
print(f"删除结果: {result}") # 输出: 删除结果: True
print(f"删除后数组: {arr}") # 输出: [0, 5, 3, 7, 1, 6]「删除元素」需要移动后续元素,移动次数与数组长度相关,因此时间复杂度为 。
3. 总结
数组是一种基础且重要的数据结构,采用连续的内存空间来存储同类型的数据。其最大优势在于支持随机访问,可以通过下标高效地定位和访问任意元素。
数组的访问和修改操作时间复杂度为 ,而插入和删除操作由于需要移动元素,时间复杂度为 。
4. 练习题目
参考资料
- 【文章】数据结构中的数组和不同语言中数组的区别 - CSDN 博客
- 【文章】数组理论基础 - 代码随想录
- 【文章】Python 与 Java 中容器对比:List - 知乎
- 【文章】什么是数组 - 漫画算法 - 小灰的算法之旅 - 力扣
- 【文章】数组 - 数据结构与算法之美 - 极客时间
- 【书籍】数据结构教程 第 2 版 - 唐发根 著
- 【书籍】数据结构与算法 Python 语言描述 - 裘宗燕 著