1.4 选择排序

---

1. 选择排序算法思想

选择排序（Selection Sort）基本思想：

将数组分为两个区间：左侧为已排序区间，右侧为未排序区间。每趟从未排序区间中选择最小的元素，放到已排序区间的末尾。

选择排序是一种简单直观的排序算法，实现简单，易于理解。

2. 选择排序算法步骤

假设数组长度为 $n$，选择排序的算法步骤如下：

1. 初始状态：已排序区间为空，未排序区间为 $[0, n - 1]$。
2. 第 $i$ 趟选择（$i$ 从 $1$ 开始）：
   1. 在未排序区间 $[i - 1, n - 1]$ 中找到最小元素的位置 $min\_i$。
   2. 将位置 $i - 1$ 的元素与位置 $min\_i$ 的元素交换。
   3. 此时 $[0, i - 1]$ 为已排序区间，$[i, n - 1]$ 为未排序区间。
3. 重复步骤 2，直到未排序区间为空，排序完成。

以数组 $[5, 2, 3, 6, 1, 4]$ 为例，演示一下选择排序的算法步骤。

<1>

选择排序 1

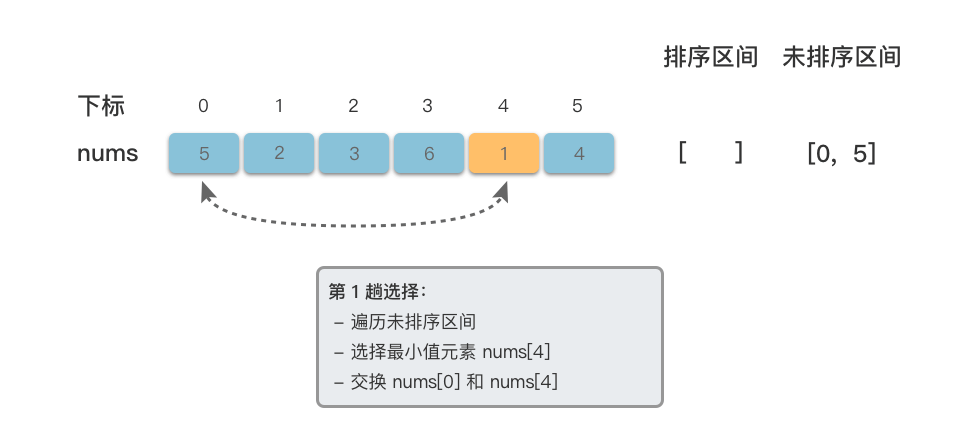
<2>

选择排序 2

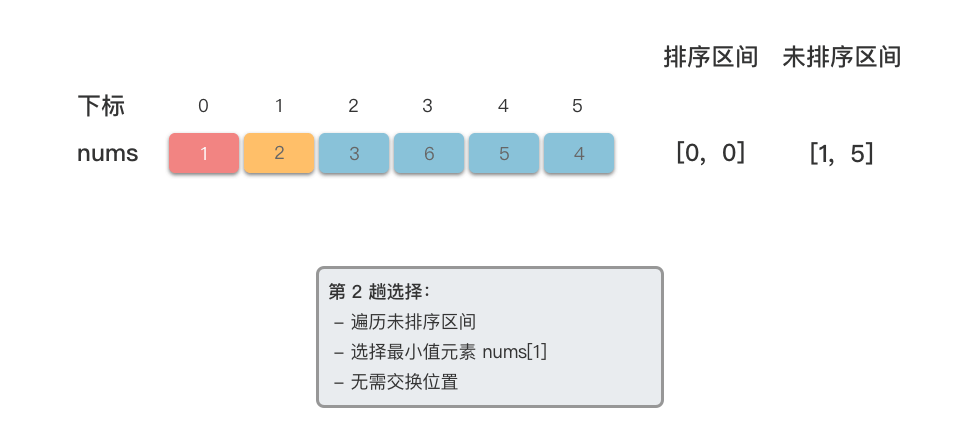
<3>

选择排序 3

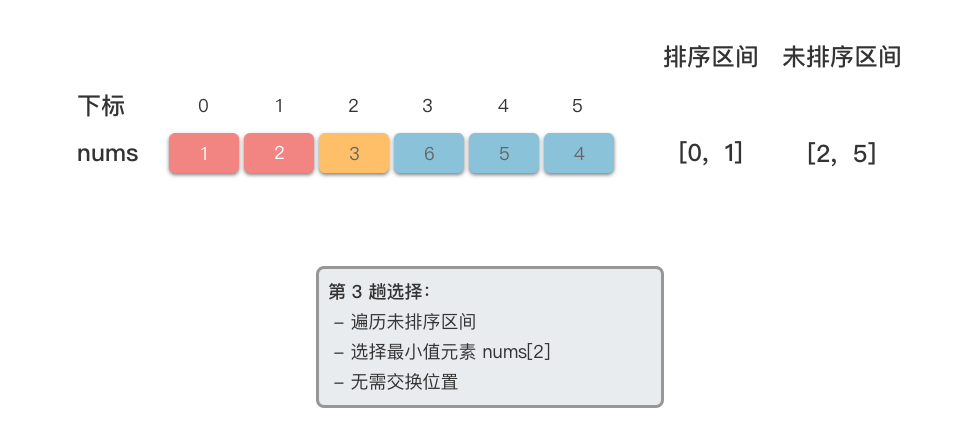
<4>

选择排序 4

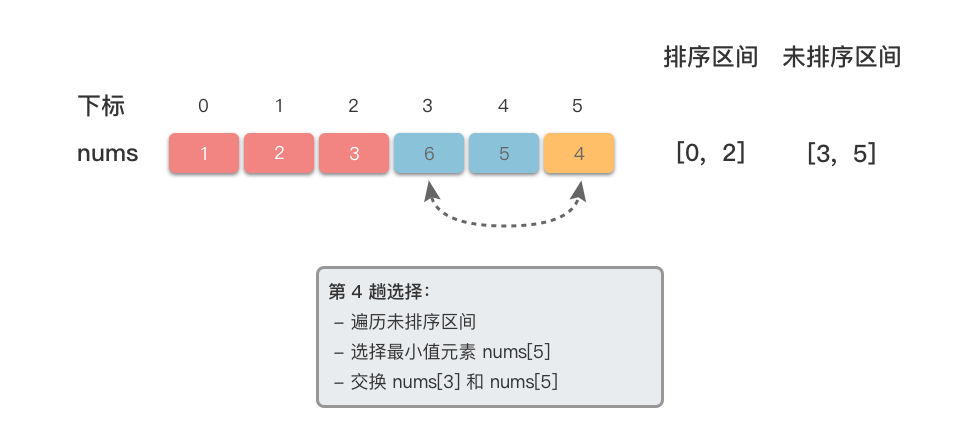
<5>

选择排序 5

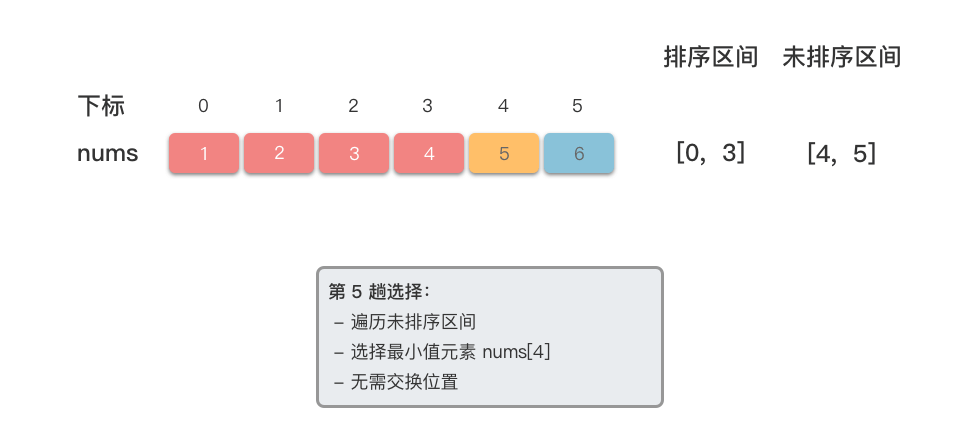
<6>

选择排序 6

<7>

选择排序 7

3. 选择排序代码实现

class Solution:
    def selectionSort(self, nums: [int]) -> [int]:
        n = len(nums)
        for i in range(n - 1):
            # 找到未排序区间中最小元素的位置
            min_i = i
            for j in range(i + 1, n):
                if nums[j] < nums[min_i]:
                    min_i = j
            # 交换元素
            if i != min_i:
                nums[i], nums[min_i] = nums[min_i], nums[i]
        return nums

    def sortArray(self, nums: [int]) -> [int]:
        return self.selectionSort(nums)

4. 选择排序算法分析

指标	复杂度	说明
最佳时间复杂度	$O(n^2)$	无论数组状态如何，都需要 $\frac{n(n-1)}{2}$ 次比较
最坏时间复杂度	$O(n^2)$	无论数组状态如何，都需要 $\frac{n(n-1)}{2}$ 次比较
平均时间复杂度	$O(n^2)$	选择排序的时间复杂度与数据状态无关
空间复杂度	$O(1)$	原地排序，只使用常数空间
稳定性	❌ 不稳定	交换操作可能改变相等元素的相对顺序

适用场景：

• 数据量较小（$n < 50$）
• 对空间复杂度要求严格的场景

5. 总结

选择排序是一种简单直观的排序算法，通过不断选择未排序区间的最小元素来构建有序序列。

优点：实现简单，空间复杂度低，交换次数少
缺点：时间复杂度高，不适合大规模数据

练习题目

• 0912. 排序数组（选择排序会超时，仅作练习）

• 排序算法题目列表