1.6 希尔排序

---

1. 希尔排序算法思想

希尔排序（Shell Sort）基本思想：

通过设定不同的间隔（gap），将数组分组进行插入排序，然后逐步缩小间隔直至为 $1$，最终完成整个数组的排序。

2. 希尔排序算法步骤

假设数组长度为 $n$，算法步骤如下：

1. 设定初始间隔 gap = n / 2。
2. 按间隔将数组分组，对每组进行插入排序。
3. 缩小间隔 gap = gap / 2。
4. 重复步骤 $2 \sim 3$，直到 gap = 1。
5. 最后对整个数组进行一次插入排序。

以数组 $[7, 2, 6, 8, 0, 4, 1, 5, 9, 3]$ 为例，演示一下希尔排序的算法步骤。

<1>

希尔排序 1

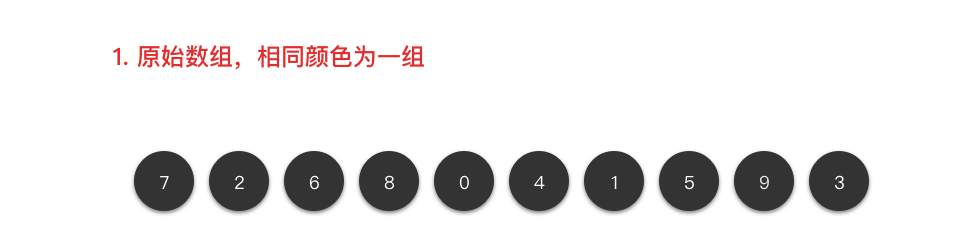
<2>

希尔排序 2

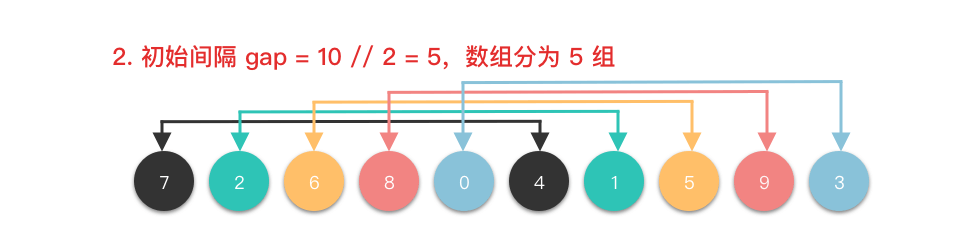
<3>

希尔排序 3

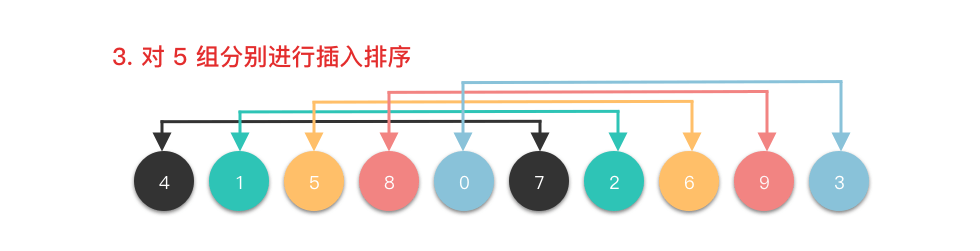
<4>

希尔排序 4

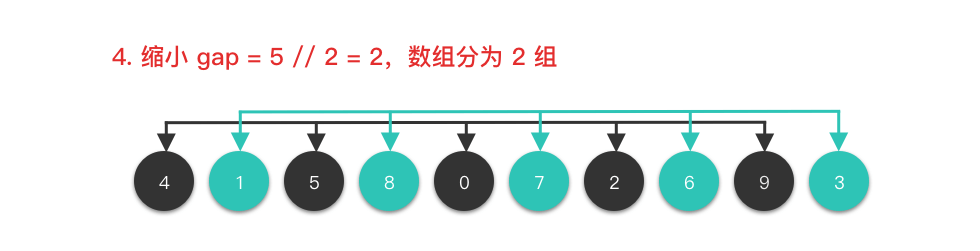
<5>

希尔排序 5

<6>

希尔排序 6

<7>

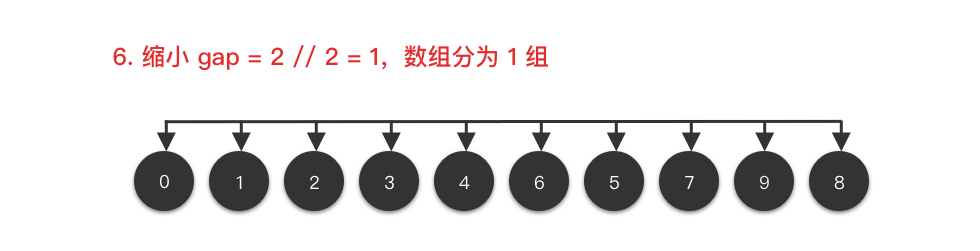
希尔排序 7

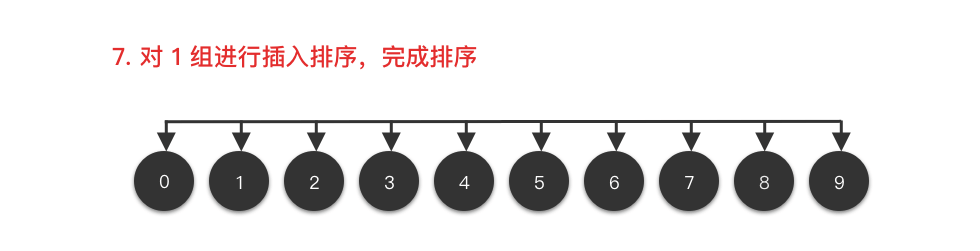
3. 希尔排序代码实现

class Solution:
    def shellSort(self, nums: [int]) -> [int]:
        size = len(nums)
        gap = size // 2  # 初始间隔设为数组长度的一半

        # 不断缩小gap，直到gap为0
        while gap > 0:
            # 从gap位置开始，对每个元素进行组内插入排序
            for i in range(gap, size):
                temp = nums[i]  # 记录当前待插入的元素
                j = i
                # 在组内进行插入排序，将比 temp 大的元素向后移动
                while j >= gap and nums[j - gap] > temp:
                    nums[j] = nums[j - gap]  # 元素后移
                    j -= gap    # 向前跳 gap 步
                nums[j] = temp  # 插入到正确位置
            # 缩小 gap，通常取 gap 的一半
            gap //= 2

        return nums  # 返回排序后的数组

    def sortArray(self, nums: [int]) -> [int]:
        """排序接口，调用shellSort方法"""
        return self.shellSort(nums)

4. 希尔排序算法分析

指标	复杂度	说明
最佳时间复杂度	$O(n)$	当数组已有序时
最坏时间复杂度	$O(n^2)$	使用普通间隔序列时
平均时间复杂度	$O(n^{1.3})$ ~ $O(n^{1.5})$	取决于间隔序列选择，若选取得当接近于 $O(n \log n)$
空间复杂度	$O(1)$	原地排序，只使用常数空间
稳定性	❌ 不稳定	不同组间的相等元素可能改变相对顺序

补充说明：

• 希尔排序的时间复杂度高度依赖于间隔序列的选择。
• 当采用常见的 gap = gap // 2 间隔序列时，排序过程大约需要 $\log_2 n$ 趟，每一趟的操作类似于分组插入排序。
• 每一趟的排序时间复杂度约为 $O(n)$，但随着 gap 的减小，实际操作次数逐步减少。
• 综合来看，希尔排序的整体时间复杂度通常介于 $O(n \log n)$ 和 $O(n^2)$ 之间，若间隔序列选择得当，性能可接近 $O(n \log n)$。

适用场景：

• 中等规模数据（$50 \leq n \leq 1000$）
• 对插入排序的改进需求
• 对稳定性要求不高的场景

5. 总结

希尔排序是插入排序的改进版本，通过分组排序减少数据移动次数，提高排序效率。

优点：比插入排序更快，空间复杂度低，适合中等规模数据
缺点：时间复杂度不稳定，不稳定排序，间隔序列选择影响性能

练习题目

• 0912. 排序数组

• 0506. 相对名次

• 排序算法题目列表