1.8 快速排序

ITCharge大约 4 分钟

1.8 快速排序

---

1. 快速排序算法思想

快速排序（Quick Sort）基本思想：
采用分治策略，选择一个基准元素，将数组分为两部分：小于基准的元素放在左侧，大于基准的元素放在右侧。然后递归地对左右两部分进行排序，最终得到有序数组。

2. 快速排序算法步骤

快速排序的核心是 分区操作，具体步骤如下：

选择基准：从数组中选择一个元素作为基准值（通常选择第一个元素）
分区操作：
- 使用双指针法，左指针从数组开始，右指针从数组末尾
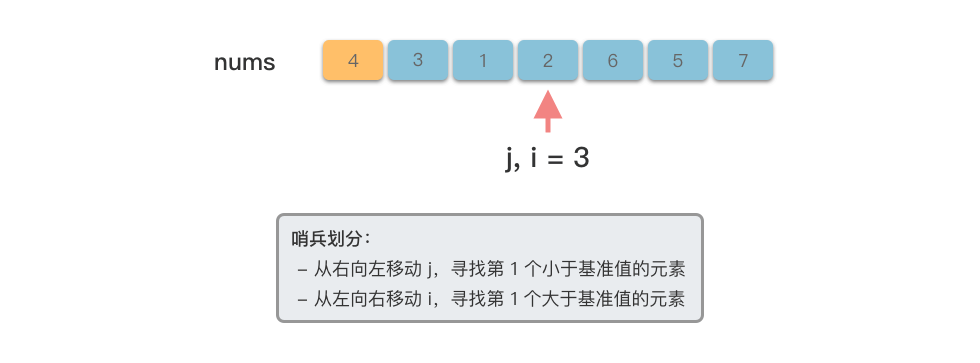
- 右指针向左移动，找到第一个小于基准值的元素
- 左指针向右移动，找到第一个大于基准值的元素
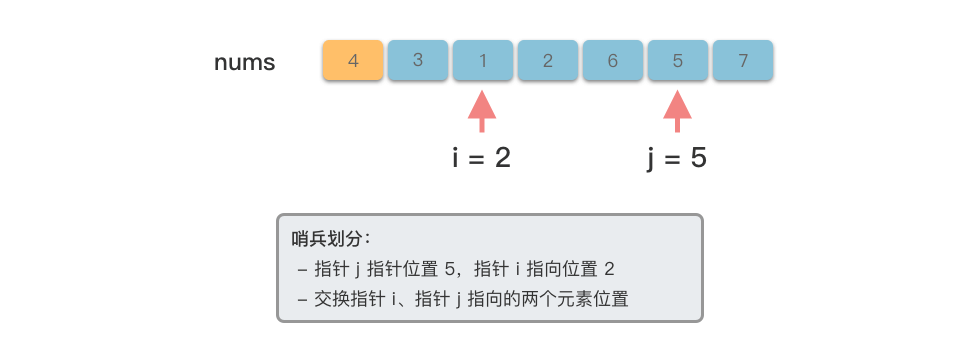
- 交换这两个元素
- 重复上述过程，直到左右指针相遇
- 将基准值放到正确位置（左右指针相遇处）
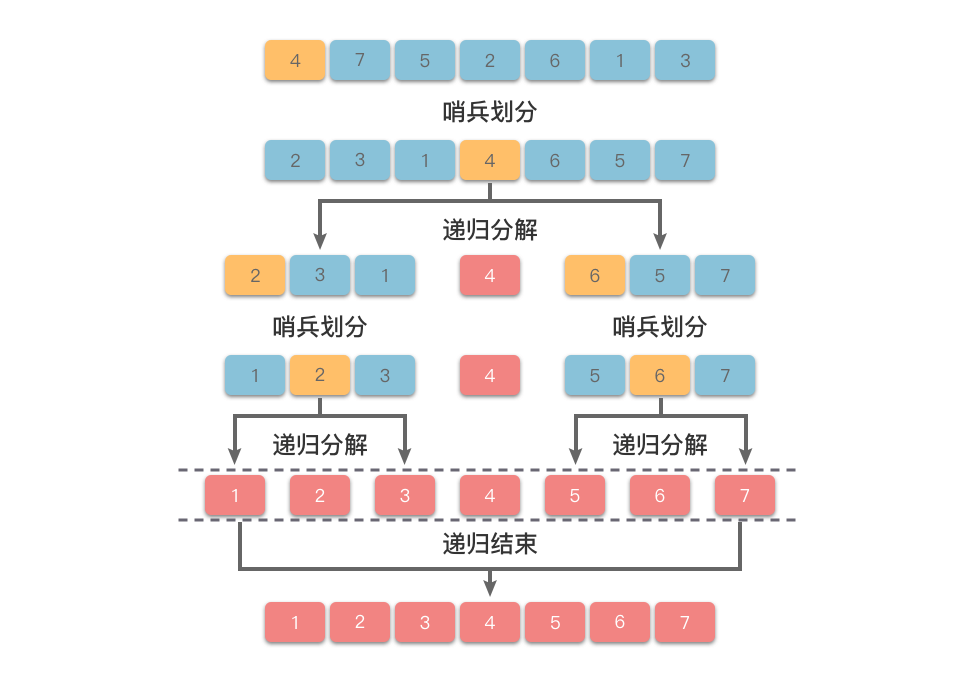
递归排序：对基准值左右的两个子数组分别进行快速排序

以数组 $[4, 7, 5, 2, 6, 1, 3]$ 为例，先来演示一下快速排序的分区操作过程。

<1>

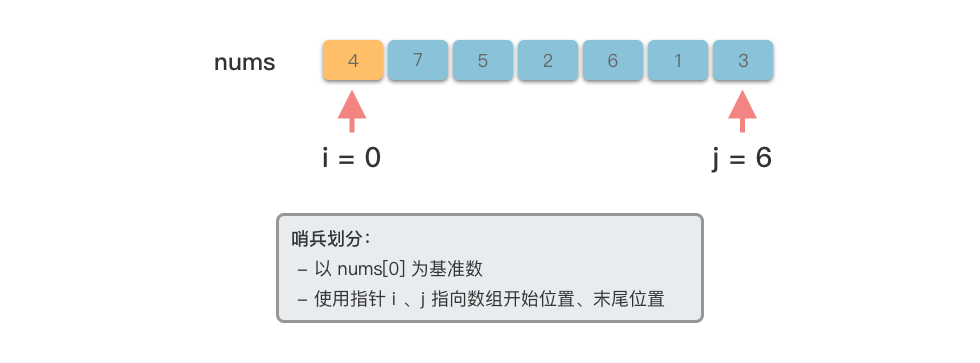
<2>

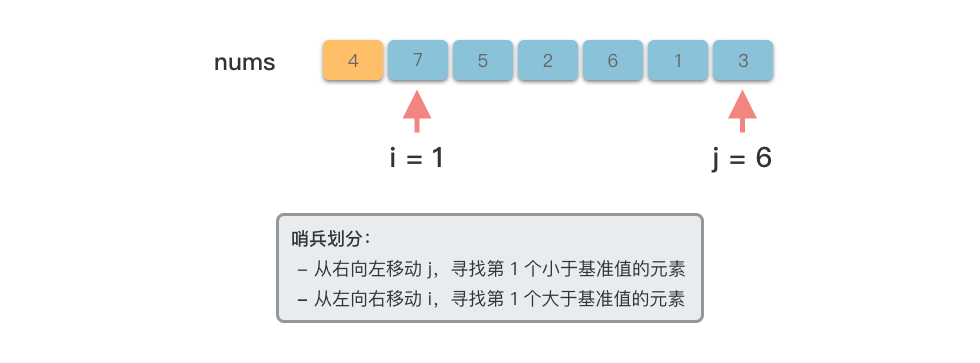
<3>

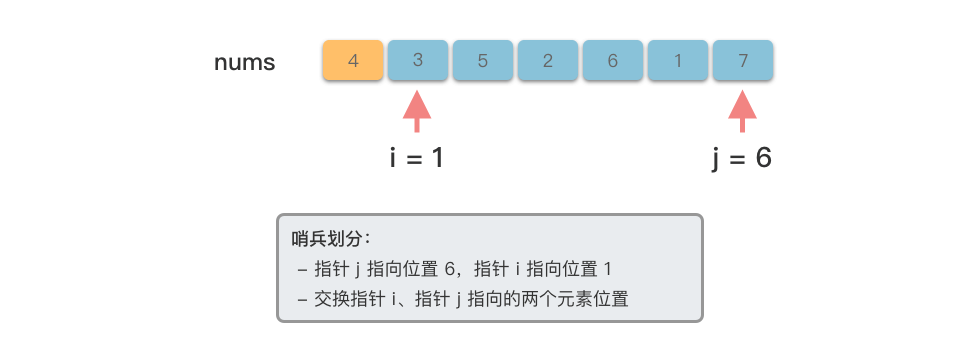
<4>

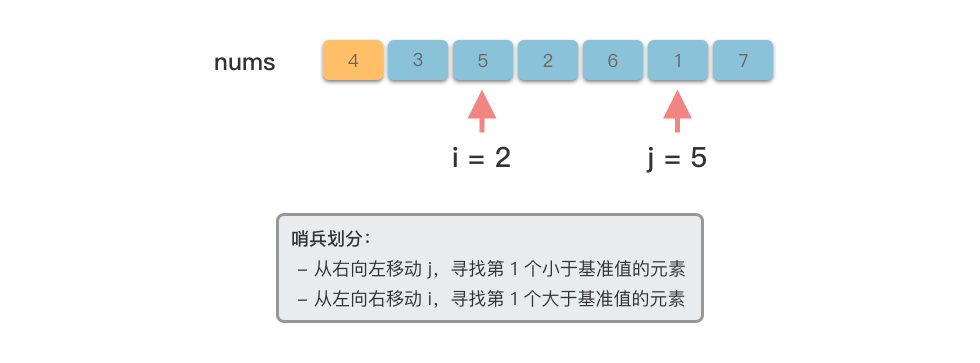
<5>

<6>

<7>

完成一次分区后，数组被分为三部分：左子数组、基准值、右子数组。然后递归地对左右子数组进行排序。

3. 快速排序代码实现

import random

class Solution:
    def randomPartition(self, nums: [int], low: int, high: int) -> int:
        # 随机选择基准值，避免最坏情况
        i = random.randint(low, high)
        # 将基准数与最低位互换
        nums[i], nums[low] = nums[low], nums[i]
        # 以最低位为基准数，然后将数组中比基准数大的元素移动到基准数右侧，比他小的元素移动到基准数左侧。最后将基准数放到正确位置上
        return self.partition(nums, low, high)
    
    # 哨兵划分：以第 1 位元素 nums[low] 为基准数，然后将比基准数小的元素移动到基准数左侧，将比基准数大的元素移动到基准数右侧，最后将基准数放到正确位置上
    def partition(self, nums: [int], low: int, high: int) -> int:
        pivot = nums[low]  # 基准值
        i, j = low, high
        
        while i < j:
            # 从右向左找小于基准值的元素
            while i < j and nums[j] >= pivot:
                j -= 1
            # 从左向右找大于基准值的元素
            while i < j and nums[i] <= pivot:
                i += 1
            # 交换元素
            nums[i], nums[j] = nums[j], nums[i]
        
        # 将基准值放到正确位置
        nums[i], nums[low] = nums[low], nums[i]
        # 返回基准数的索引
        return i

    def quickSort(self, nums: [int], low: int, high: int) -> [int]:
        if low < high:
            # 分区并获取基准值位置
            pivot_i = self.randomPartition(nums, low, high)
            # 递归排序左右子数组
            self.quickSort(nums, low, pivot_i - 1)
            self.quickSort(nums, pivot_i + 1, high)
        return nums

    def sortArray(self, nums: [int]) -> [int]:
        return self.quickSort(nums, 0, len(nums) - 1)

4. 快速排序算法分析

指标	复杂度	说明
最佳时间复杂度	$O(n \log n)$	每次都能将数组平均分成两半
最坏时间复杂度	$O(n^2)$	每次选择的基准值都是极值（如已排序数组）
平均时间复杂度	$O(n \log n)$	随机选择基准值时的期望复杂度
空间复杂度	$O(\log n)$	递归栈空间，最坏情况下为 $O(n)$
稳定性	❌ 不稳定	交换操作可能改变相等元素的相对位置