1.9 堆排序
1.9 堆排序
---1. 堆结构
「堆排序(Heap sort)」是一种基于「堆结构」实现的高效排序算法。在介绍堆排序之前,我们先来了解什么是堆结构。
1.1 堆的定义
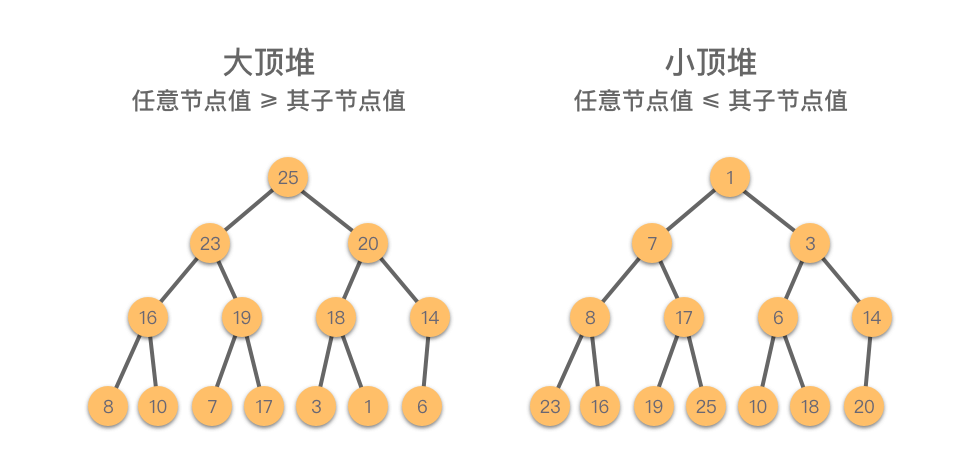
堆(Heap):一种特殊的完全二叉树,具有以下性质之一:
- 大顶堆(Max Heap):任意节点值 ≥ 其子节点值
- 小顶堆(Min Heap):任意节点值 ≤ 其子节点值
1.2 堆的存储结构
堆的逻辑结构是一棵完全二叉树,如下图所示:
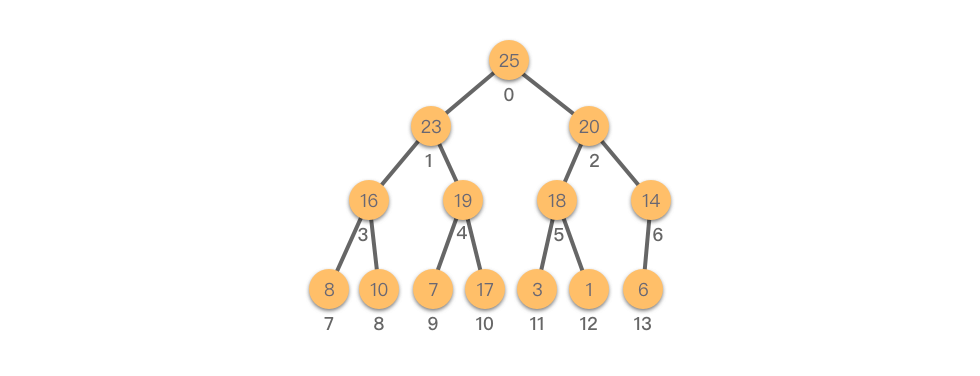
在实际编程中,堆通常采用数组进行存储。使用数组表示堆时,节点与数组索引之间的对应关系如下:
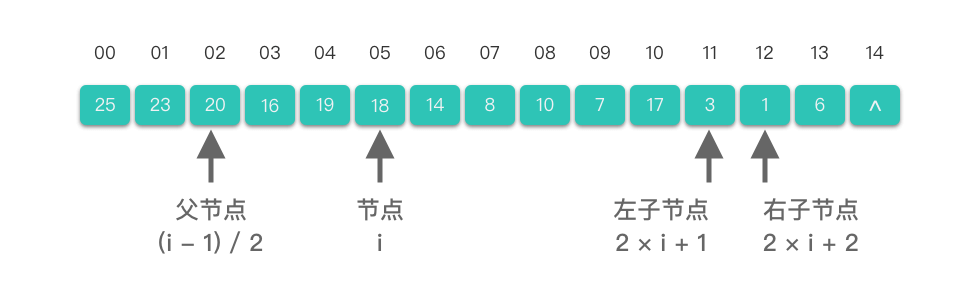
- 如果某节点的下标为 ,则其左孩子的下标为 ,右孩子的下标为 ;
- 如果某节点的下标为 ,则其父节点的下标为 。
如下图所示,顺序存储结构(数组)可以高效地表示堆:
1.3 堆的基本操作
1.3.1 创建空堆
创建空堆:初始化一个空的堆结构,为后续的堆操作做准备。
创建空堆是堆操作的基础,只需要初始化一个空数组即可。在实际应用中,我们通常创建一个类来封装堆的各种操作。
class MaxHeap:
def __init__(self):
# 创建空的大顶堆
self.max_heap = []时间复杂度:。空堆创建只需要初始化一个空数组,操作非常简单高效。
1.3.2 访问堆顶元素
访问堆顶元素:获取堆中最大(或最小)的元素,即根节点的值。
在大顶堆中,堆顶元素就是整个堆中的最大值;在小顶堆中,堆顶元素就是整个堆中的最小值。由于堆顶元素总是存储在数组的第一个位置,因此访问操作非常高效。
def peek(self) -> int:
# 检查堆是否为空
if not self.max_heap:
return None
# 返回堆顶元素(数组第一个元素)
return self.max_heap[0]时间复杂度:。由于堆顶元素始终位于数组索引 0 的位置,访问操作只需要一次数组索引操作,不依赖于堆的大小。
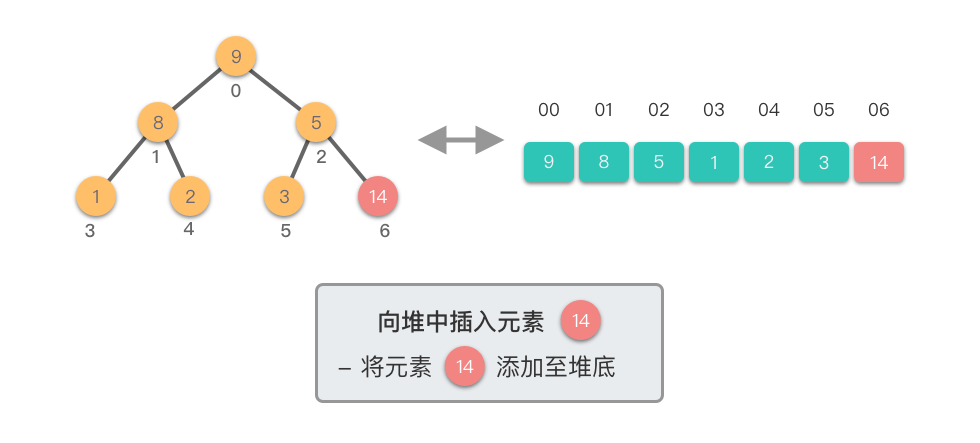
1.3.3 向堆中插入元素
向堆中插入元素:将新元素添加到堆中,并通过调整保持堆的性质。
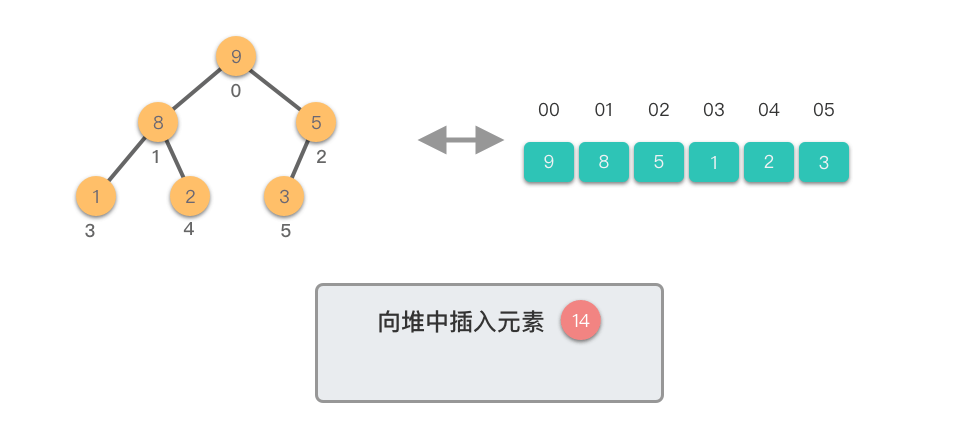
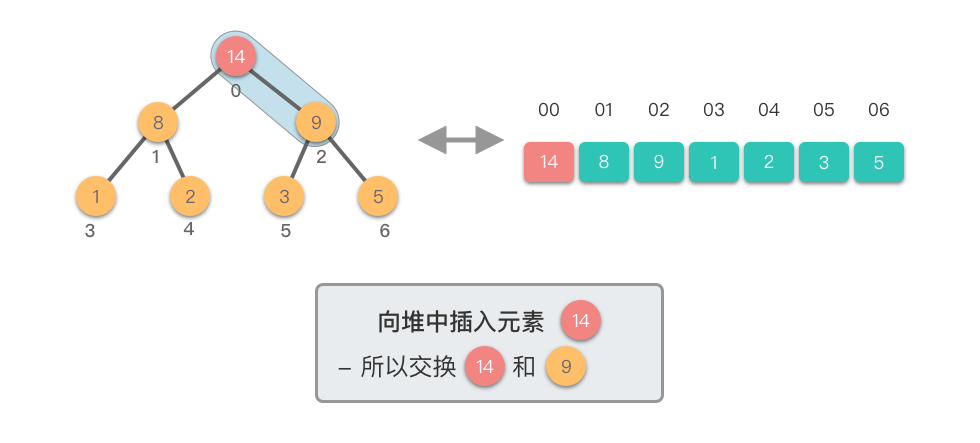
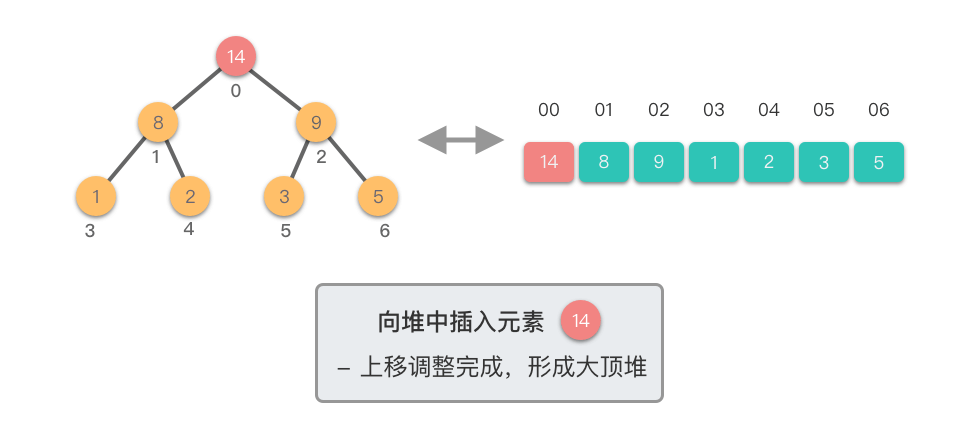
向堆中插入元素需要两个步骤:
- 添加元素:将新元素添加到堆的末尾,保持完全二叉树的结构
- 上移调整:从新元素开始向上调整,直到满足堆的性质
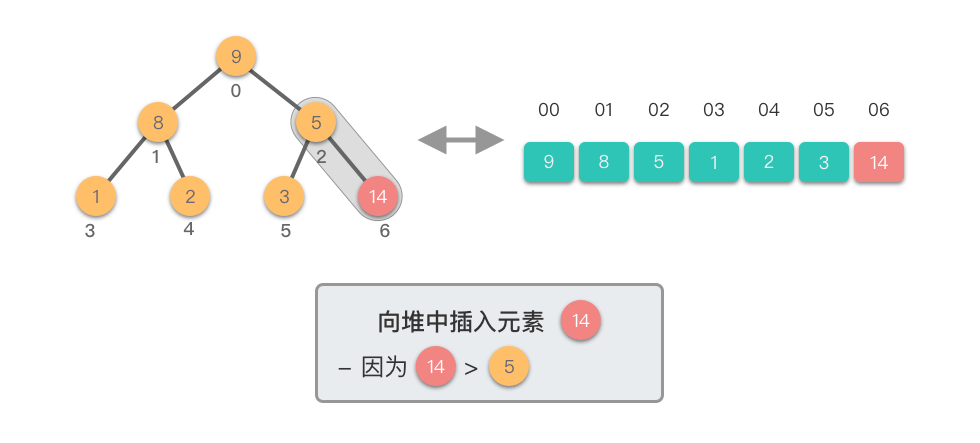
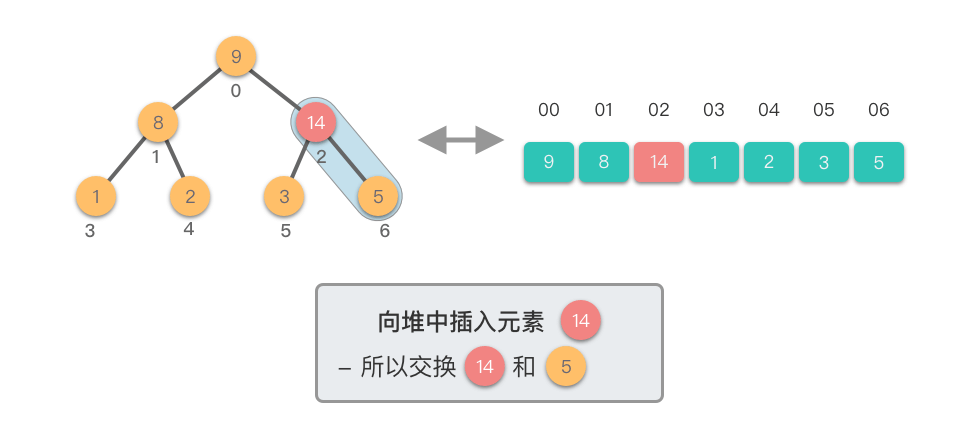
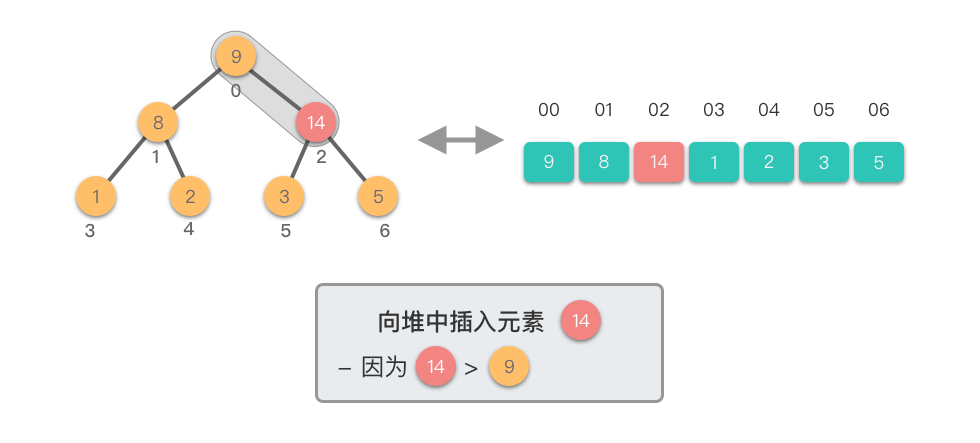
上移调整(Shift Up)过程:
- 将新插入的节点与其父节点比较
- 如果新节点值大于父节点值,则交换它们
- 重复此过程,直到新节点不再大于其父节点或到达根节点
下面我们通过图示步骤来演示一下向堆中插入元素的过程。
def push(self, val: int):
# 将新元素添加到堆的末尾
self.max_heap.append(val)
# 从新元素开始进行上移调整
self.__shift_up(len(self.max_heap) - 1)
def __shift_up(self, i: int):
# 上移调整:将节点与其父节点比较并交换
while (i - 1) // 2 >= 0 and self.max_heap[i] > self.max_heap[(i - 1) // 2]:
# 交换当前节点与父节点
self.max_heap[i], self.max_heap[(i - 1) // 2] = self.max_heap[(i - 1) // 2], self.max_heap[i]
# 继续向上调整
i = (i - 1) // 2时间复杂度:。在最坏情况下,新插入的元素需要从堆的底部移动到顶部,移动的距离等于堆的高度 。
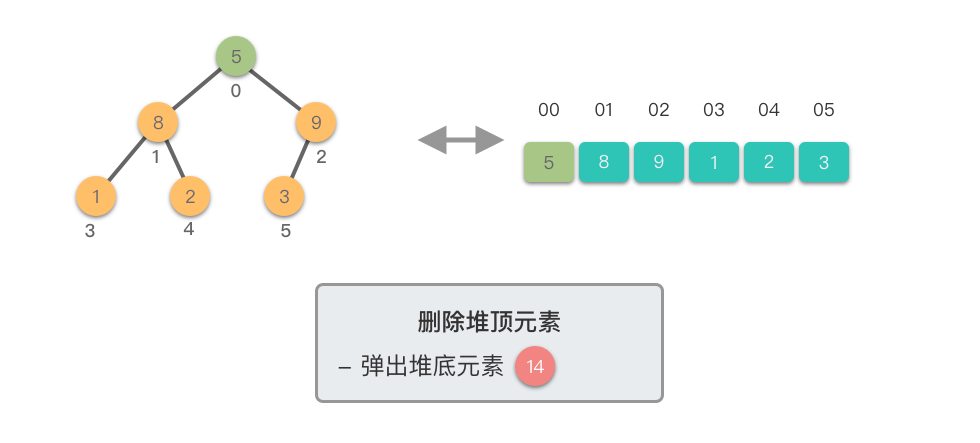
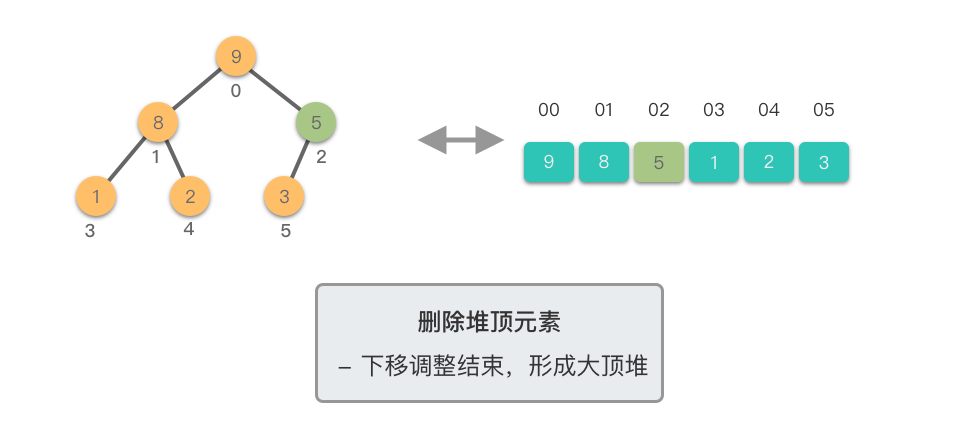
1.3.4 删除堆顶元素
删除堆顶元素:移除堆中的最大(或最小)元素,并重新调整堆结构。
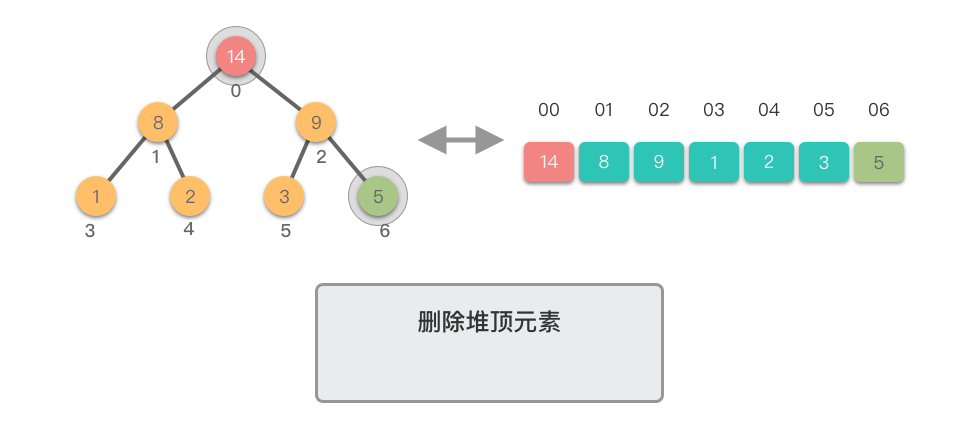
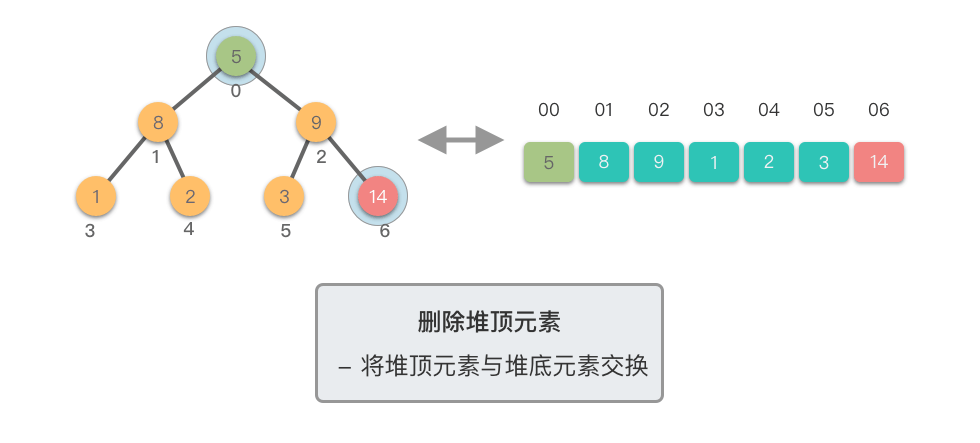
删除堆顶元素需要三个步骤:
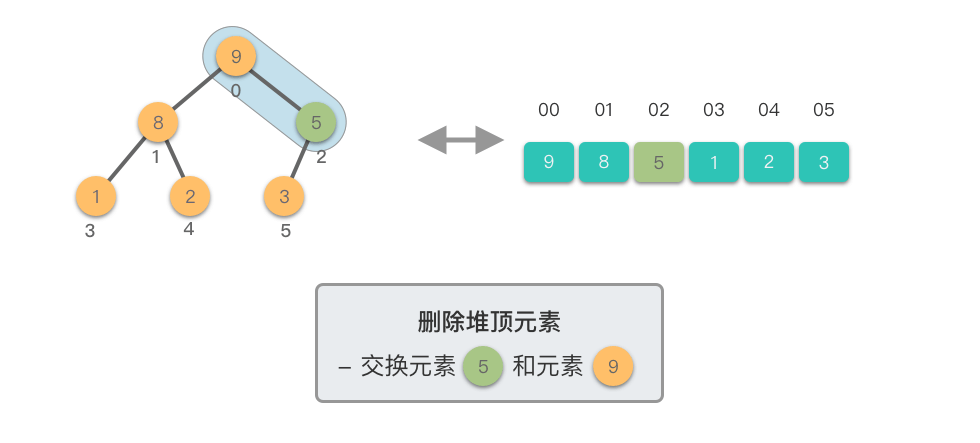
- 交换元素:将堆顶元素与末尾元素交换
- 删除元素:移除末尾元素(原堆顶元素)
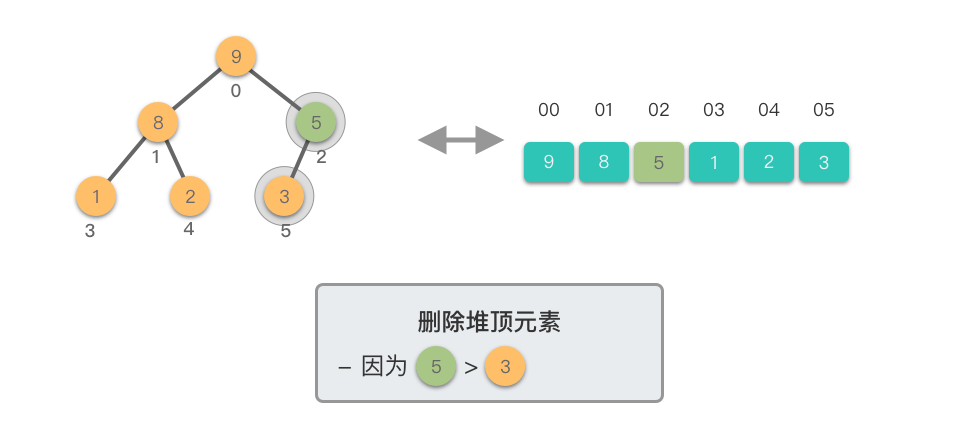
- 下移调整:从新的堆顶开始向下调整,直到满足堆的性质
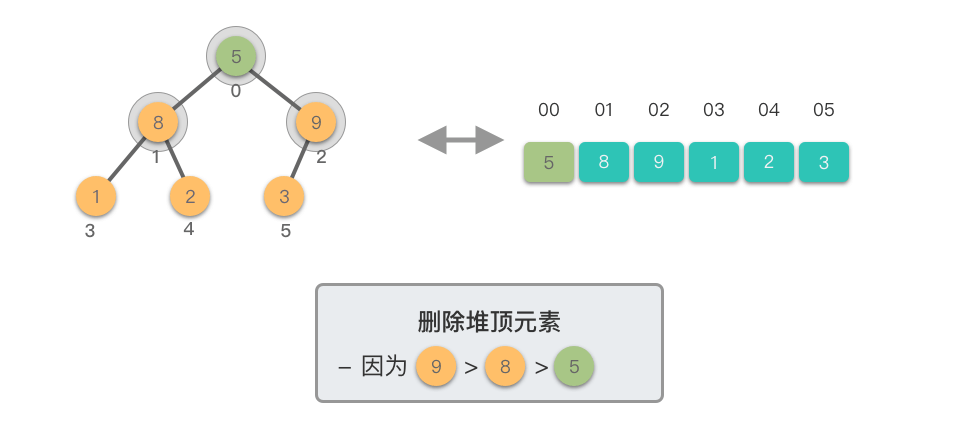
下移调整(Shift Down)过程:
- 将新的堆顶元素与其较大的子节点比较
- 如果堆顶元素小于较大子节点,则交换它们
- 重复此过程,直到堆顶元素不再小于其子节点或到达叶子节点
这个过程称为「下移调整」,因为新的堆顶元素会逐步向堆的下方移动,直到找到合适的位置。
下面我们通过图示步骤来演示一下删除堆顶元素的过程。
def pop(self) -> int:
# 检查堆是否为空
if not self.max_heap:
raise IndexError("堆为空")
# 交换堆顶元素与末尾元素
size = len(self.max_heap)
self.max_heap[0], self.max_heap[size - 1] = self.max_heap[size - 1], self.max_heap[0]
# 删除末尾元素(原堆顶元素)
val = self.max_heap.pop()
# 如果堆不为空,进行下移调整
if self.max_heap:
self.__shift_down(0, len(self.max_heap))
# 返回被删除的堆顶元素
return val
def __shift_down(self, i: int, n: int):
# 下移调整:将节点与其较大的子节点比较并交换
while 2 * i + 1 < n:
# 计算左右子节点索引
left, right = 2 * i + 1, 2 * i + 2
# 找出较大的子节点
larger = left
if right < n and self.max_heap[right] > self.max_heap[left]:
larger = right
# 如果当前节点小于较大子节点,则交换
if self.max_heap[i] < self.max_heap[larger]:
self.max_heap[i], self.max_heap[larger] = self.max_heap[larger], self.max_heap[i]
i = larger
else:
break时间复杂度:。在最坏情况下,新的堆顶元素需要从堆的顶部移动到底部,移动的距离等于堆的高度 。
2. 堆排序
2.1 堆排序算法思想
堆排序(Heap sort)基本思想:
利用堆的特性,将数组构建成大顶堆,然后重复取出堆顶元素(最大值)并调整堆结构,最终得到有序数组。
2.2 堆排序算法步骤
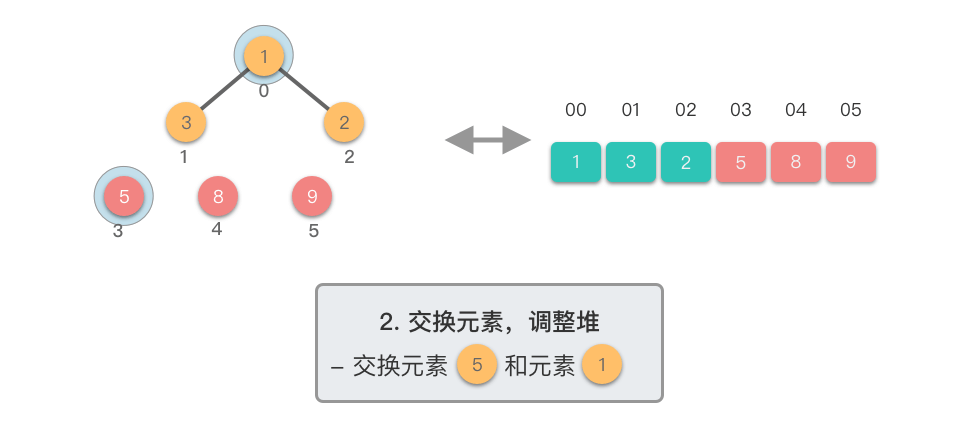
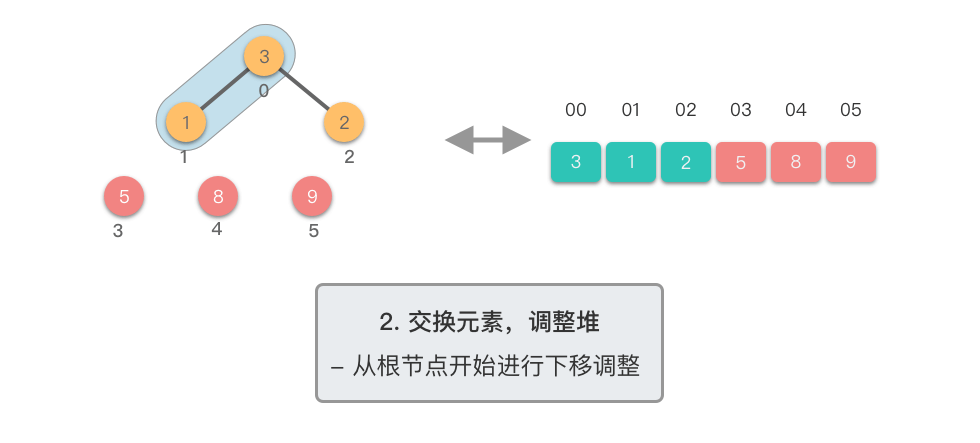
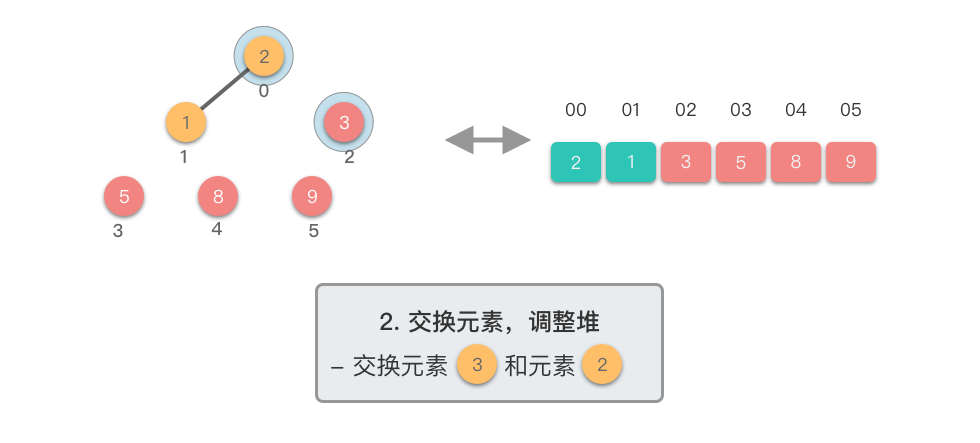
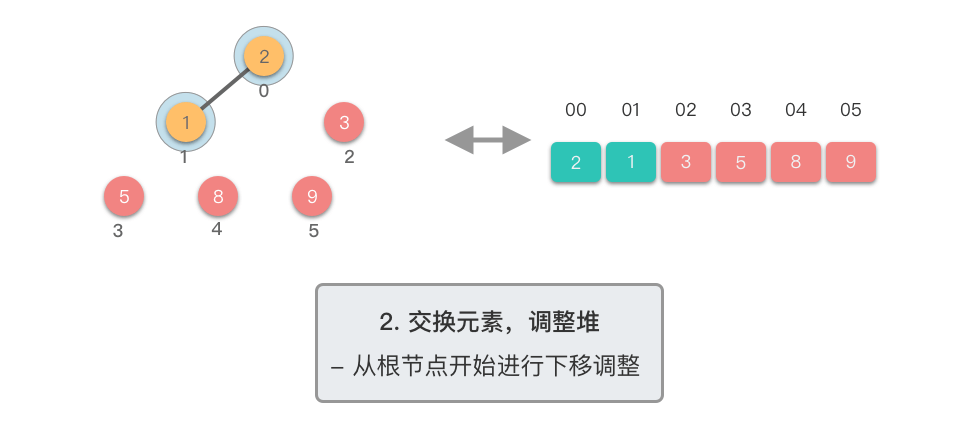
堆排序分为两个主要阶段:
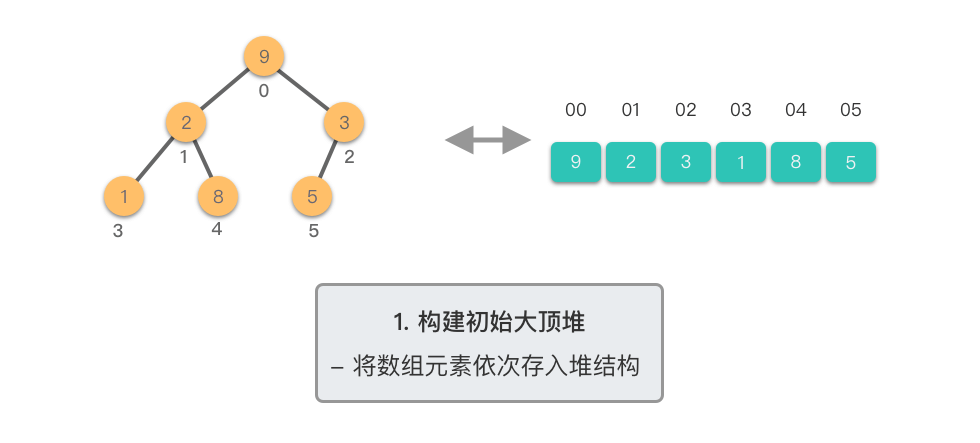
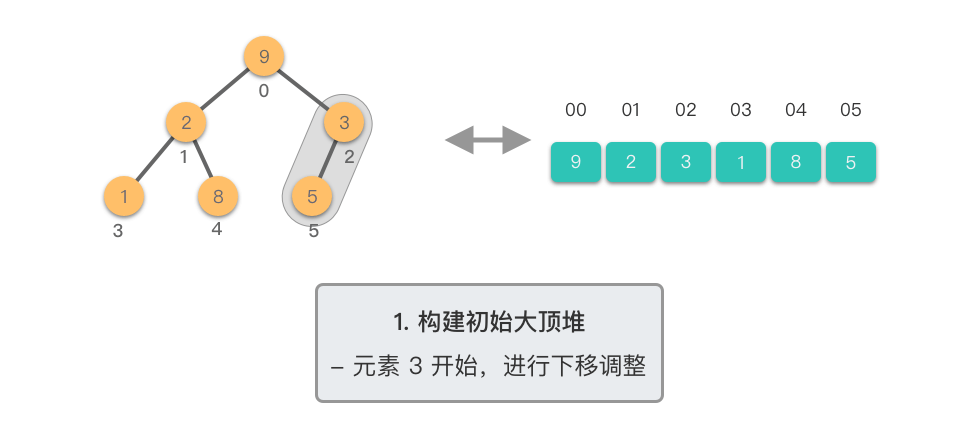
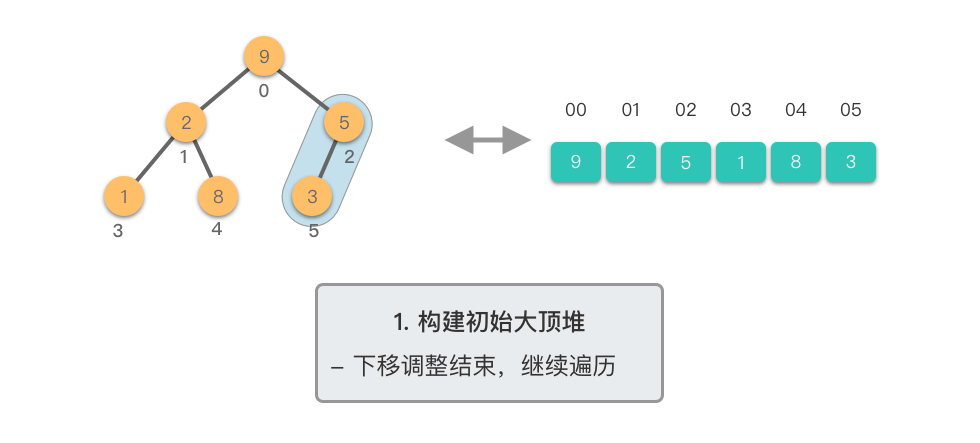
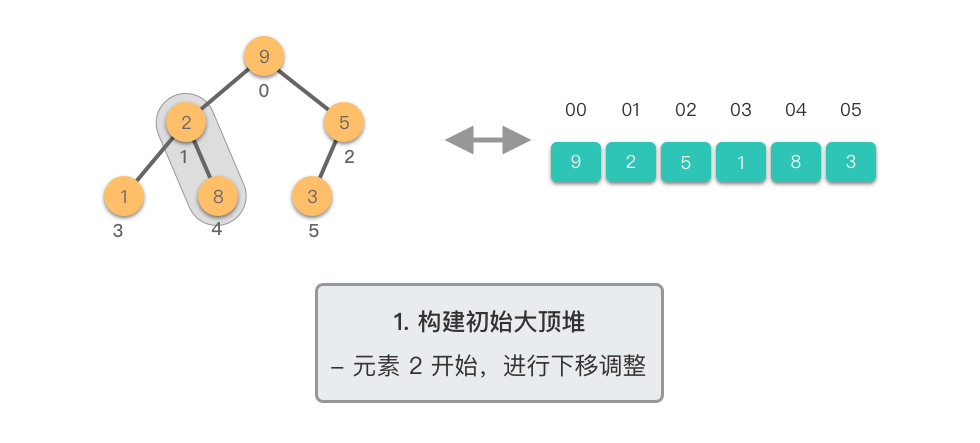
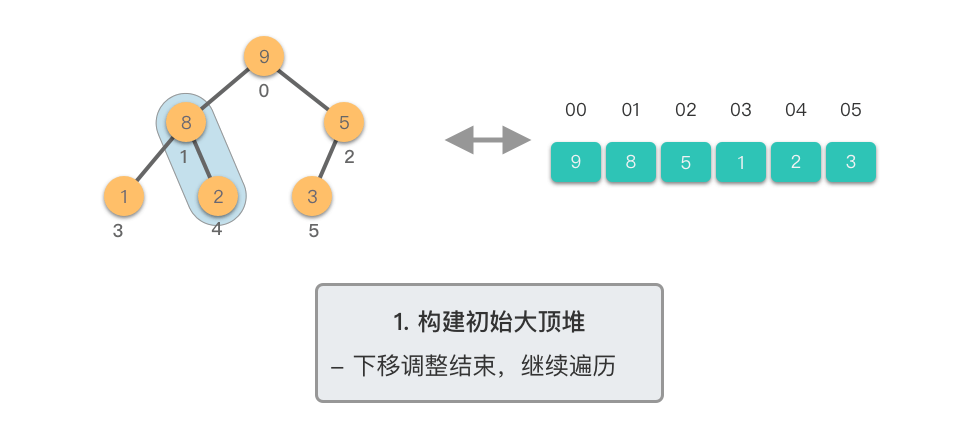
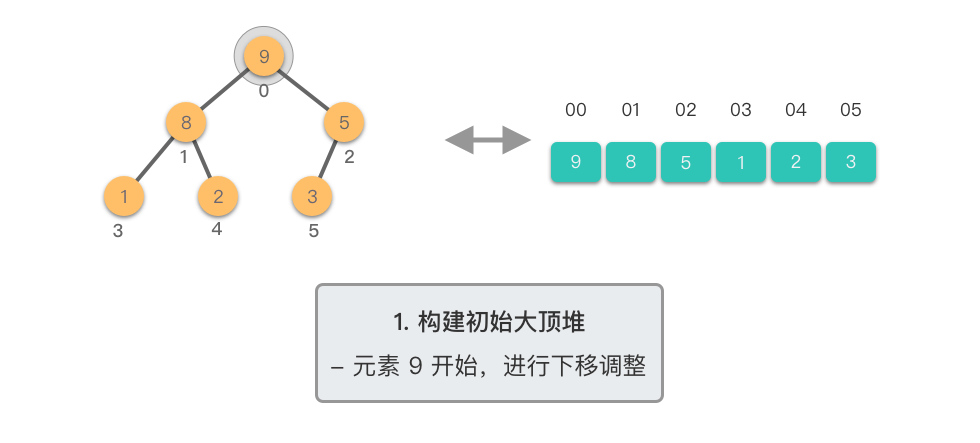
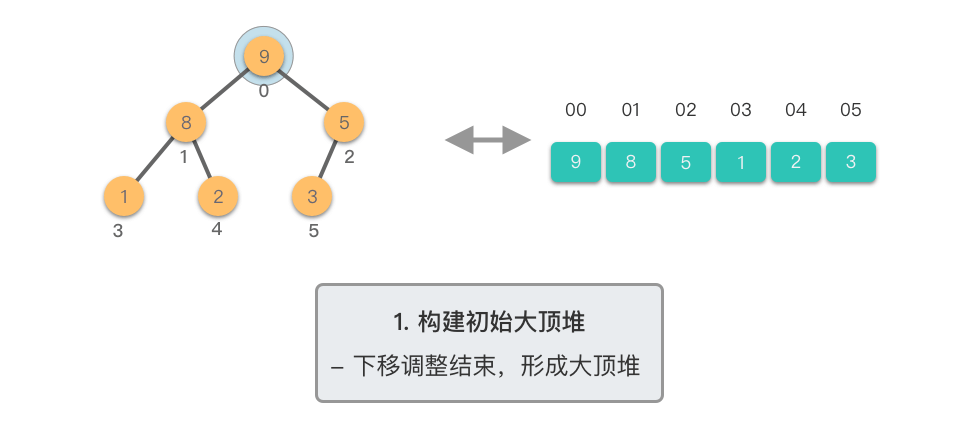
第一阶段:构建初始大顶堆
- 将原始数组视为完全二叉树
- 从最后一个非叶子节点开始,自底向上进行下移调整
- 将数组转换为大顶堆
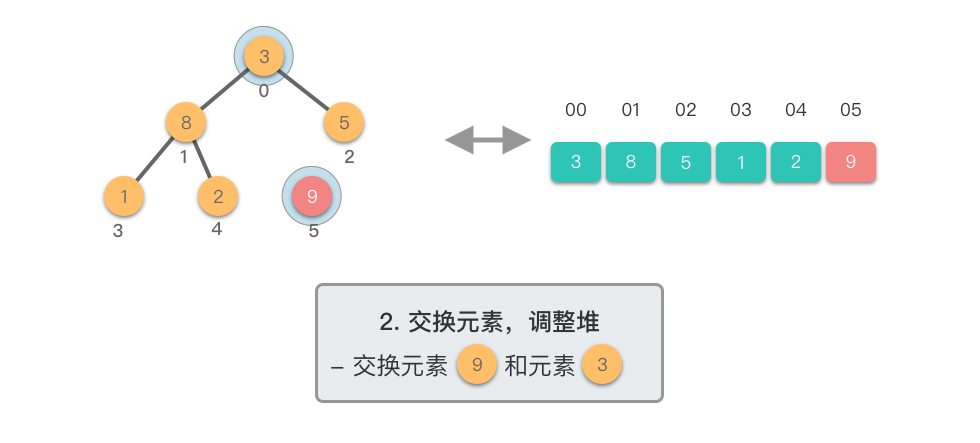
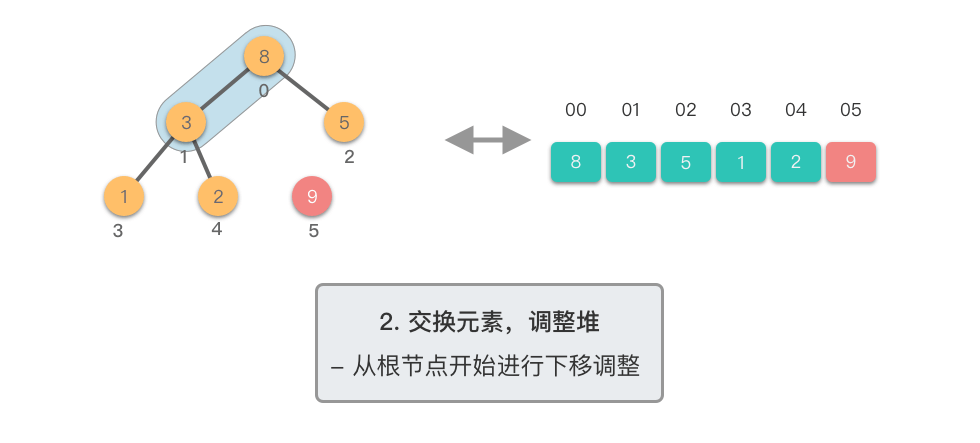
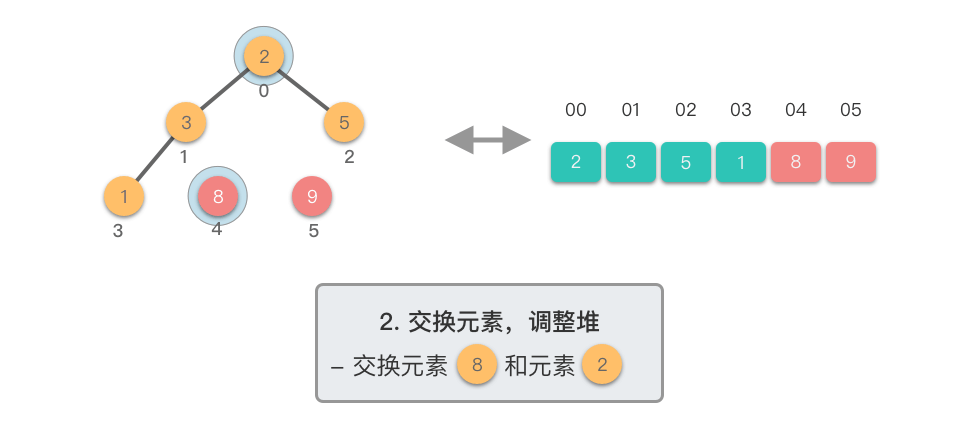
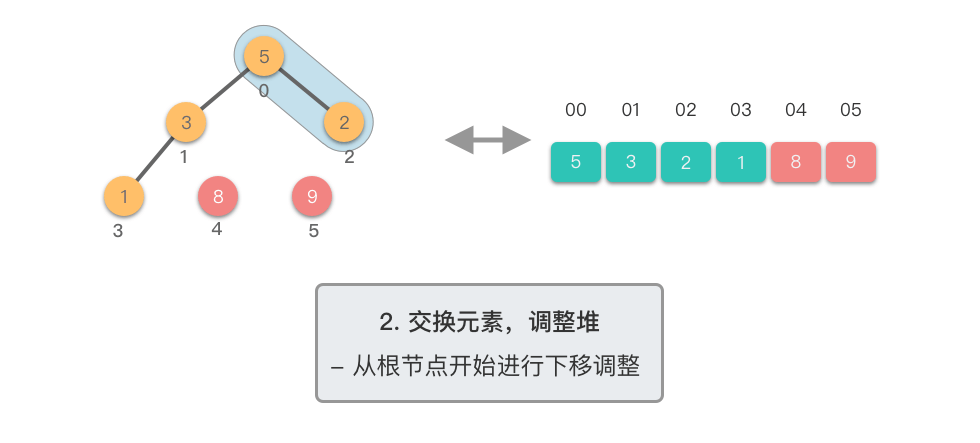
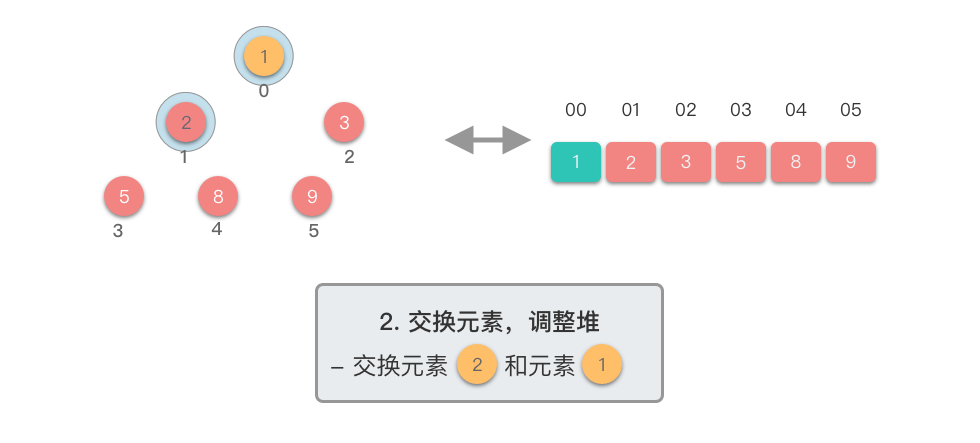
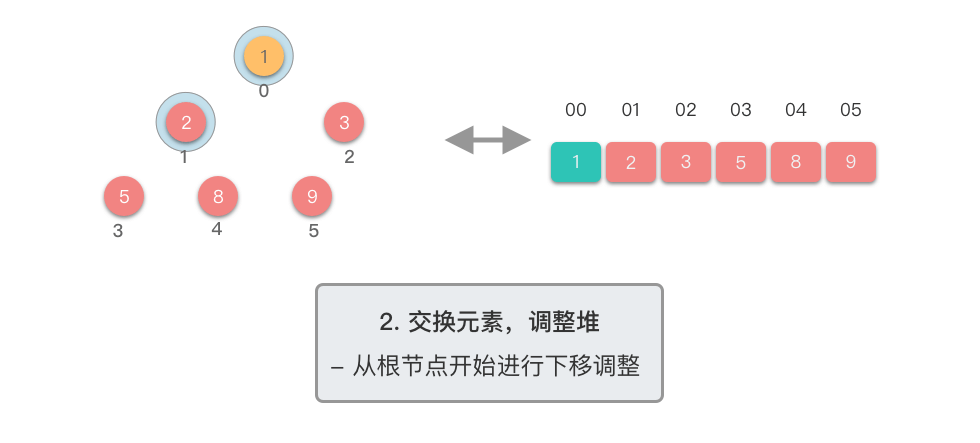
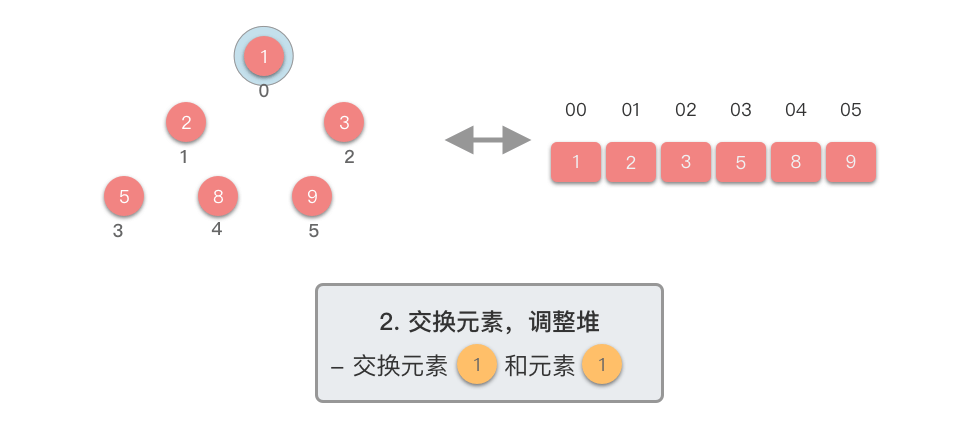
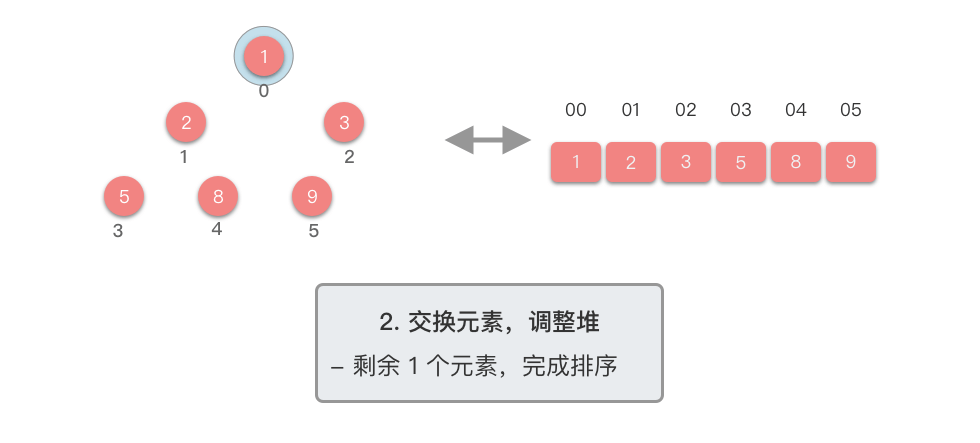
第二阶段:重复提取最大值
- 交换堆顶元素与当前末尾元素
- 堆长度减 ,末尾元素已排好序
- 对新的堆顶元素进行下移调整,恢复堆的性质
- 重复步骤 ,直到堆的大小为
2.3 堆排序代码实现
class MaxHeap:
def __init__(self):
self.max_heap = []
def __buildMaxHeap(self, nums: [int]):
# 将数组元素复制到堆中
self.max_heap = nums.copy()
size = len(nums)
# 从最后一个非叶子节点开始,自底向上构建堆
for i in range((size - 2) // 2, -1, -1):
self.__shift_down(i, size)
def maxHeapSort(self, nums: [int]) -> [int]:
# 第一阶段:构建初始大顶堆
self.__buildMaxHeap(nums)
size = len(self.max_heap)
# 第二阶段:重复提取最大值
for i in range(size - 1, -1, -1):
# 交换堆顶元素与当前末尾元素
self.max_heap[0], self.max_heap[i] = self.max_heap[i], self.max_heap[0]
# 对新的堆顶元素进行下移调整,堆的大小为 i
self.__shift_down(0, i)
# 返回排序后的数组
return self.max_heap
def __shift_down(self, i: int, n: int):
# 下移调整:将节点与其较大的子节点比较并交换
while 2 * i + 1 < n:
left, right = 2 * i + 1, 2 * i + 2
# 找出较大的子节点
larger = left
if right < n and self.max_heap[right] > self.max_heap[left]:
larger = right
# 如果当前节点小于较大子节点,则交换
if self.max_heap[i] < self.max_heap[larger]:
self.max_heap[i], self.max_heap[larger] = self.max_heap[larger], self.max_heap[i]
i = larger
else:
break
class Solution:
def sortArray(self, nums: [int]) -> [int]:
return MaxHeap().maxHeapSort(nums)2.4 堆排序算法分析
时间复杂度分析:
堆排序的时间复杂度由两个主要步骤组成:
构建初始堆:
- 从最后一个非叶子节点开始,自底向上进行下移调整
- 对于第 层的节点,最多需要下移 层
- 第 层有 个节点
- 总调整次数:
重复提取最大值:
- 需要进行 次提取操作
- 每次提取后需要下移调整,最坏情况下需要 时间
- 总时间复杂度:
总时间复杂度:
| 指标 | 复杂度 | 说明 |
|---|---|---|
| 最佳时间复杂度 | 无论数组状态如何,都需要构建堆和提取元素 | |
| 最坏时间复杂度 | 无论数组状态如何,都需要构建堆和提取元素 | |
| 平均时间复杂度 | 堆排序的时间复杂度与数据状态无关 | |
| 空间复杂度 | 原地排序,只使用常数空间 | |
| 稳定性 | 不稳定 | 调整堆的过程中可能改变相等元素的相对顺序 |
适用场景:
- 大规模数据排序
- 内存受限的环境
- 需要稳定时间复杂度的场景
- 需要保证最坏情况下性能的场景
3. 总结
堆排序是一种基于堆数据结构的排序算法,利用堆的特性实现高效排序。
核心思想:
- 将数组构建成大顶堆,堆顶元素始终是最大值
- 重复取出堆顶元素并调整堆结构,最终得到有序数组
算法步骤:
- 构建初始堆:将数组转换为大顶堆
- 重复提取:交换堆顶与末尾元素,调整堆结构,逐步得到有序数组
- 优点:
- 时间复杂度稳定,始终为
- 空间复杂度低,为
- 适合处理大规模数据
- 原地排序,不需要额外空间
- 缺点:
- 不稳定排序
- 常数因子较大,实际应用中可能比快速排序稍慢
- 对缓存不友好,访问模式不够局部化
堆排序是一种同时具备 时间复杂度和 空间复杂度的比较排序算法,在内存受限或需要稳定时间复杂度的场景下具有重要价值。