1.10 计数排序

---

1. 计数排序算法思想

计数排序（Counting Sort）基本思想：

统计数组中每个元素出现的次数，然后根据统计信息将元素按顺序放置到正确位置，实现排序。

2. 计数排序算法步骤

1. 确定数值范围：找出数组中的最大值和最小值，计算数值范围。
2. 创建计数数组：创建一个大小为数值范围的数组，用于统计每个元素出现的次数。
3. 统计元素频次：遍历原数组，统计每个元素出现的次数。
4. 计算累积频次：将计数数组转换为累积频次数组，表示每个元素在排序后数组中的位置。
5. 逆序填充结果：逆序遍历原数组，根据累积频次将元素放入正确位置。

以数组 $[3, 0, 4, 2, 5, 1, 3, 1, 4, 5]$ 为例，演示一下计数排序的算法步骤。

计数排序的算法步骤

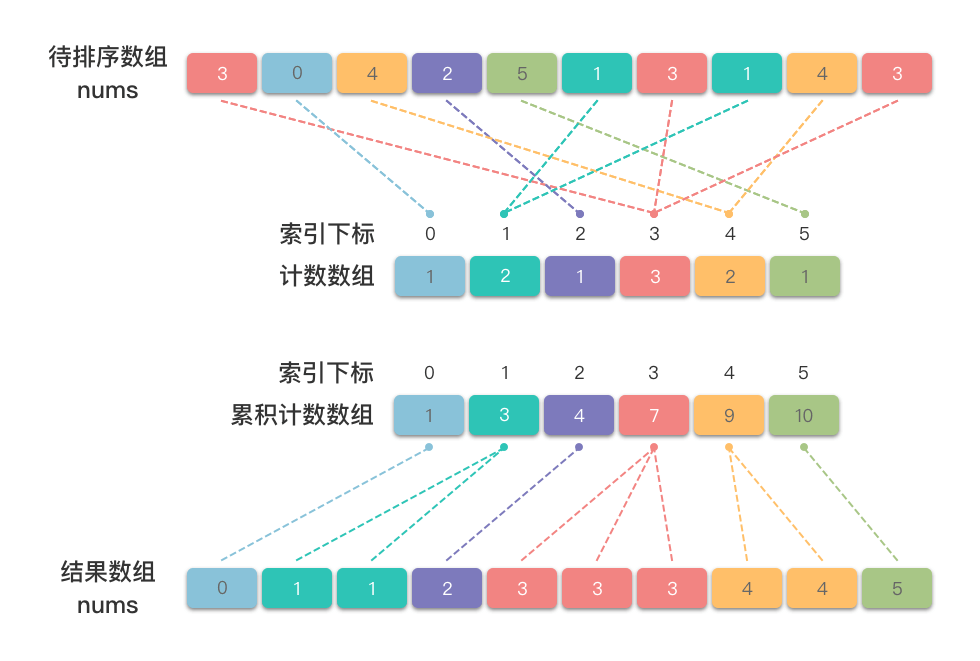
3. 计数排序代码实现

class Solution:
    def countingSort(self, nums: [int]) -> [int]:
        # 确定数值范围
        nums_min, nums_max = min(nums), max(nums)
        size = nums_max - nums_min + 1
        counts = [0 for _ in range(size)]
        
        # 统计每个元素出现的次数
        for num in nums:
            counts[num - nums_min] += 1
        
        # 计算累积频次（每个元素出现的次数）
        for i in range(1, size):
            counts[i] += counts[i - 1]

        # 逆序填充结果数组
        res = [0 for _ in range(len(nums))]
        for i in range(len(nums) - 1, -1, -1):
            num = nums[i]
            # 根据累积计数数组，将 num 放在数组对应位置
            res[counts[num - nums_min] - 1] = num
            counts[num - nums_min] -= 1

        return res

    def sortArray(self, nums: [int]) -> [int]:
        return self.countingSort(nums)

4. 计数排序算法分析

指标	复杂度	说明
最佳时间复杂度	$O(n + k)$	$n$ 为元素个数，$k$ 为数值范围，无论数组状态如何，都需要统计和填充操作
最坏时间复杂度	$O(n + k)$	无论数组状态如何，都需要统计和填充操作
平均时间复杂度	$O(n + k)$	计数排序的时间复杂度与数据状态无关
空间复杂度	$O(k)$	需要额外的计数数组，大小取决于数值范围
稳定性	✅ 稳定	逆序填充保持相等元素的相对顺序

适用场景：

• 整数排序
• 数值范围较小（$k$ 远小于 $n$）
• 对稳定性有要求的场景

5. 总结

计数排序是一种非比较排序算法，通过统计元素频次实现排序。它特别适合数值范围较小的整数排序。

优点：时间复杂度稳定，稳定排序，适合小范围整数排序
缺点：空间复杂度与数值范围相关，不适合大范围数值

练习题目

• 0912. 排序数组

• 1122. 数组的相对排序

• 排序算法题目列表