1.15 数组双指针

ITCharge大约 12 分钟

1.15 数组双指针

---

1. 双指针简介

双指针（Two Pointers）：在遍历序列时，同时用两个指针协同访问元素，以高效解决问题。常见类型有三种：同序列相向移动的「对撞指针」、同序列同向移动的「快慢指针」、以及分别指向不同序列的「分离双指针」。

在处理数组区间类问题时，传统的暴力解法时间复杂度通常为 $O(n^2)$ ，而双指针方法能够利用区间的「单调性」特征，将时间复杂度优化至 $O(n)$ 。

2. 对撞指针

对撞指针：即用两个指针 $left$ 和 $right$ ，分别指向序列的首尾， $left$ 向右、 $right$ 向左移动，直到两指针相遇（ $left == right$ ）或满足特定条件。

2.1 对撞指针求解步骤

初始化两个指针 $left = 0$ ， $right = len(nums) - 1$ 。
循环中根据条件移动指针：若满足某条件， $left$ 右移；若满足另一条件， $right$ 左移。
循环至两指针相遇或满足终止条件。

2.2 对撞指针通用模板

# 初始化左右指针，分别指向数组的首尾
left, right = 0, len(nums) - 1

# 当左指针小于右指针时循环
while left < right:
    # 如果满足题目要求的特殊条件，直接返回结果
    if 满足要求的特殊条件:
        return 符合条件的值 
    # 如果满足某一条件，左指针右移，缩小区间
    elif 一定条件 1:
        left += 1
    # 如果满足另一条件，右指针左移，缩小区间
    elif 一定条件 2:
        right -= 1

# 如果循环结束还未找到，返回未找到或对应值
return 没找到 或 找到对应值

2.3 对撞指针适用场景

对撞指针常用于有序数组或字符串，典型应用包括：

查找有序数组中特定元素组合，如二分查找、两数之和等。
字符串或数组反转，如反转字符串、判断回文、颠倒二进制等。

下面通过具体例子演示对撞指针的用法。

2.4 经典例题：两数之和 II - 输入有序数组

2.4.1 题目链接

167. 两数之和 II - 输入有序数组 - 力扣（LeetCode）

2.4.2 题目大意

描述：给定一个下标从 $1$ 开始计数、升序排列的整数数组： $numbers$ 和一个目标值 $target$ 。

要求：从数组中找出满足相加之和等于 $target$ 的两个数，并返回两个数在数组中下的标值。

说明：

$2 \le numbers.length \le 3 * 10^4$ 。
$-1000 \le numbers[i] \le 1000$ 。
$numbers$ 按非递减顺序排列。
$-1000 \le target \le 1000$ 。
仅存在一个有效答案。

示例：

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

2.4.3 解题思路

思路 1：暴力枚举

可以直接使用两重循环，枚举所有可能的两数组合，判断其和是否等于目标值 $target$ 。具体做法如下：

外层循环遍历数组的每一个元素 $i$ 。
内层循环遍历 $i$ 之后的每一个元素 $j$ 。
判断 $numbers[i] + numbers[j]$ 是否等于 $target$ ，如果相等则返回 $[i + 1, j + 1]$ （题目下标从 1 开始）。
如果遍历结束仍未找到，返回 $[-1, -1]$ 。

思路 1：代码

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        size = len(numbers)
        for i in range(size):
            for j in range(i + 1, size):
                if numbers[i] + numbers[j] == target:
                    return [i + 1, j + 1]
        return [-1, -1]

思路 1：复杂度分析

时间复杂度： $O(n^2)$ 。外层循环 $O(n)$ ，内层循环最坏情况下 $O(n)$ ，因此总时间复杂度为 $O(n^2)$ 。
空间复杂度： $O(1)$ 。只使用了常数级别的额外空间。

思路 2：对撞指针

可以考虑使用对撞指针来减少时间复杂度。具体做法如下：

使用两个指针 $left$ ， $right$ 。 $left$ 指向数组第一个值最小的元素位置， $right$ 指向数组值最大元素位置。
判断两个位置上的元素的和与目标值的关系。
1. 如果元素和等于目标值，则返回两个元素位置。
2. 如果元素和大于目标值，则让 $right$ 左移，继续检测。
3. 如果元素和小于目标值，则让 $left$ 右移，继续检测。
直到 $left$ 和 $right$ 移动到相同位置停止检测。
如果最终仍没找到，则返回 $[-1, -1]$ 。

思路 2：代码

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        left = 0
        right = len(numbers) - 1
        while left < right:
            total = numbers[left] + numbers[right]
            if total == target:
                return [left + 1, right + 1]
            elif total < target:
                left += 1
            else:
                right -= 1
        return [-1, -1]

思路 2：复杂度分析

时间复杂度： $O(n)$ 。
空间复杂度： $O(1)$ 。只用到了常数空间存放若干变量。

3. 快慢指针

快慢指针：指两个指针从同一侧出发，步长不同，快指针（fast）移动更快，慢指针（slow）移动较慢。它们以不同速度遍历序列，直到快指针到达末尾、两指针相遇或满足特定条件时停止。

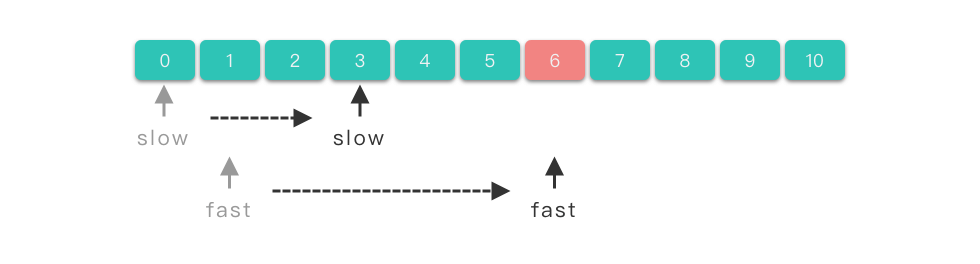
3.1 快慢指针求解步骤

初始化两个指针 $slow = 0$ ， $fast = 1$ ，分别指向第一个和第二个元素。
循环中根据条件移动指针：满足条件时 $slow += 1$ ，否则 $fast += 1$ 。
当 $fast$ 到达数组末尾、两指针相遇或满足其他条件时结束循环。

3.2 快慢指针通用模板

# 初始化慢指针 slow 和快指针 fast
slow = 0
fast = 1
# 当 fast 没有遍历到数组末尾时循环
while fast 未遍历到数组末尾：
    # 如果满足特定条件（如去重时 nums[fast] != nums[slow]）
    if 满足特定条件：
        slow += 1  # 慢指针右移一位，准备接收新元素
        # 根据实际需求，可能需要将 fast 指向的元素赋值给 slow 指向的位置
        # 例如：nums[slow] = nums[fast]
    fast += 1  # 快指针继续向右遍历
# 返回最终结果（如新数组长度 slow + 1 或处理后的数组等）
return 最终结果

3.3 快慢指针的应用场景

快慢指针主要用于解决数组元素的移动、删除等问题，以及链表中的环检测、长度统计等操作。链表相关的双指针技巧将在后续链表章节详细介绍。

接下来，我们通过具体例题，演示快慢指针的实际用法。

3.4 经典例题：删除有序数组中的重复项

3.4.1 题目链接

26. 删除有序数组中的重复项 - 力扣（LeetCode）

3.4.2 题目大意

描述：给定一个有序数组 $nums$ 。

要求：删除数组 $nums$ 中的重复元素，使每个元素只出现一次。并输出去除重复元素之后数组的长度。

说明：

不能使用额外的数组空间，在原地修改数组，并在使用 $O(1)$ 额外空间的条件下完成。

示例：

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

3.4.3 解题思路

思路 1：快慢指针

有序数组中，重复元素必然相邻。我们可以用双指针原地去重：

用两个指针 $slow$ 和 $fast$ ，初始 $slow = 0$ ， $fast = 1$ 。
遍历数组，若 $nums[fast] \neq nums[slow]$ ，则 $slow$ 右移一位，并将 $nums[fast]$ 赋值到 $nums[slow]$ 。
每轮 $fast$ 右移一位，直到遍历结束。
最终返回 $slow + 1$ ，即去重后数组长度。

思路 1：代码

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        # 数组为空或只有一个元素，直接返回长度
        if len(nums) <= 1:
            return len(nums)
        
        # slow 指针指向去重后数组的最后一个元素
        # fast 指针用于遍历整个数组
        slow, fast = 0, 1

        while fast < len(nums):
            # 如果当前 fast 指向的元素和 slow 指向的元素不同
            # 说明遇到了新的不重复元素
            if nums[slow] != nums[fast]:
                slow += 1                   # slow 前进一位
                nums[slow] = nums[fast]     # 将新元素赋值到 slow 位置
            # 无论是否赋值，fast 都要前进一位
            fast += 1
        
        # 返回去重后数组的长度（下标从0开始，所以要+1）
        return slow + 1

思路 1：复杂度分析

时间复杂度： $O(n)$ 。
空间复杂度： $O(1)$ 。

4. 分离双指针

分离双指针：指的是分别在两个不同数组上各设置一个指针，两个指针独立地在各自数组中移动，以协同完成特定任务。

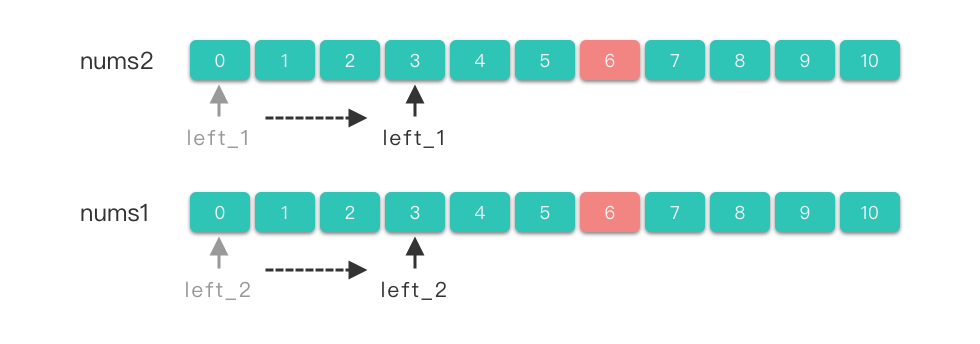
4.1 分离双指针求解步骤

定义两个指针 $left\underline{\hspace{0.5em}}1$ 和 $left\underline{\hspace{0.5em}}2$ ，分别指向两个数组的起始位置（均为 $0$ ）。
根据条件，若需要，两个指针同时右移： $left\underline{\hspace{0.5em}}1 += 1$ ， $left\underline{\hspace{0.5em}}2 += 1$ 。
若只需移动第一个数组指针，则 $left\underline{\hspace{0.5em}}1 += 1$ 。
若只需移动第二个数组指针，则 $left\underline{\hspace{0.5em}}2 += 1$ 。
当任一指针遍历到数组末尾或满足终止条件时，结束循环。

4.2 分离双指针通用模板

# 初始化两个指针，分别指向两个数组的起始位置
left_1, left_2 = 0, 0

# 当两个指针都未遍历到各自数组末尾时，循环进行比较
while left_1 < len(nums1) and left_2 < len(nums2):
    if 满足条件 1:
        # 通常表示两个指针指向的元素相等
        # 此时可以将该元素加入结果集（如交集），并同时移动两个指针
        left_1 += 1
        left_2 += 1
    elif 满足条件 2:
        # 通常表示第一个数组当前元素较小
        # 只移动第一个指针，继续比较下一个元素
        left_1 += 1
    elif 满足条件 3:
        # 通常表示第二个数组当前元素较小
        # 只移动第二个指针，继续比较下一个元素
        left_2 += 1

4.3 分离双指针适用场景

分离双指针主要应用于有序数组的合并、交集、并集等问题，能够高效地同时遍历两个数组，协同完成元素的比较与处理。

下面通过具体例子，详细讲解分离双指针的实际用法。

4.4 经典例题：两个数组的交集

4.4.1 题目链接

349. 两个数组的交集 - 力扣（LeetCode）

4.4.2 题目大意

描述：给定两个数组 $nums1$ 和 $nums2$ 。

要求：返回两个数组的交集。重复元素只计算一次。

说明：

$1 \le nums1.length, nums2.length \le 1000$ 。
$0 \le nums1[i], nums2[i] \le 1000$ 。

示例：

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]
示例 2：

示例 2：

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[9,4]
解释：[4,9] 也是可通过的

4.4.3 解题思路

思路 1：分离双指针

先对 $nums1$ 和 $nums2$ 排序。
用两个指针 $left\underline{\hspace{0.5em}}1$ 、 $left\underline{\hspace{0. 5em}}2$ 分别从两个数组头部开始遍历。
若 $nums1[left\underline{\hspace{0.5em}}1] == nums2[left\underline {\hspace{0.5em}}2]$ ，将该元素（去重）加入结果，并同时右移 $left\underline{\hspace{0.5em}}1$ 、 $left\underline {\hspace{0.5em}}2$ 。
若 $nums1[left\underline{\hspace{0.5em}}1] < nums2[left\underline {\hspace{0.5em}}2]$ ，则 $left\underline{\hspace{0.5em}}1$ 右移。
若 $nums1[left\underline{\hspace{0.5em}}1] > nums2[left\underline {\hspace{0.5em}}2]$ ，则 $left\underline {\hspace{0.5em}}2$ 右移。
遍历结束后返回结果数组。

思路 1：代码

class Solution:
    def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
        nums1.sort()  # 对 nums1 进行排序
        nums2.sort()  # 对 nums2 进行排序

        left_1 = 0  # 指向 nums1 的指针
        left_2 = 0  # 指向 nums2 的指针
        res = []

        # 优化：由于数组已排序，结果去重只需判断上一个加入的元素即可
        while left_1 < len(nums1) and left_2 < len(nums2):
            if nums1[left_1] == nums2[left_2]:
                # 只有 res 为空或当前元素与上一个加入的元素不同才加入结果，避免重复
                if not res or nums1[left_1] != res[-1]:
                    res.append(nums1[left_1])
                left_1 += 1
                left_2 += 1
            elif nums1[left_1] < nums2[left_2]:
                left_1 += 1
            else:  # nums1[left_1] > nums2[left_2]
                left_2 += 1
        return res

思路 1：复杂度分析

时间复杂度： $O(n)$ 。
空间复杂度： $O(1)$ 。

5. 双指针总结

双指针主要分为三类：「对撞指针」、「快慢指针」和「分离双指针」。

对撞指针：两个指针分别从序列两端向中间移动，常用于查找有序数组中满足特定条件的元素对、字符串反转等场景。
快慢指针：两个指针从同一端出发，步长不同，常用于数组元素的移动、删除，或链表中的环检测、长度统计等问题。
分离双指针：两个指针分别遍历不同的数组或链表，适合处理有序数组的合并、交集、并集等问题。

双指针算法能够显著降低时间复杂度，通常可将暴力解法的 $O(n^2)$ 优化为 $O(n)$ 。其核心在于利用数据的有序性或问题的单调性，通过灵活移动指针，快速排除不符合条件的情况，从而减少无效计算。熟练掌握双指针技巧，可以高效解决大量数组和链表相关的问题。

练习题目

参考资料

【博文】双指针算法之快慢指针 (yanyusoul.com)
【博文】双指针算法各类基础题型总结 - 掘金
【博文】双指针 - 力扣加加 - 努力做西湖区最好的算法题解
【博文】LeetCode分类专题（四）——双指针和滑动窗口1 - iwehdio - 博客园
【博文】双指针算法各类基础题型总结 - 掘金