1.16 数组滑动窗口

ITCharge大约 9 分钟

1.16 数组滑动窗口

---

1. 滑动窗口算法简介

在计算机网络中，滑动窗口协议（Sliding Window Protocol）是传输层进行流控的一种措施，接收方通过通告发送方自己的窗口大小，从而控制发送方的发送速度，从而达到防止发送方发送速度过快而导致自己被淹没的目的。我们所要讲解的滑动窗口算法也是利用了同样的特性。

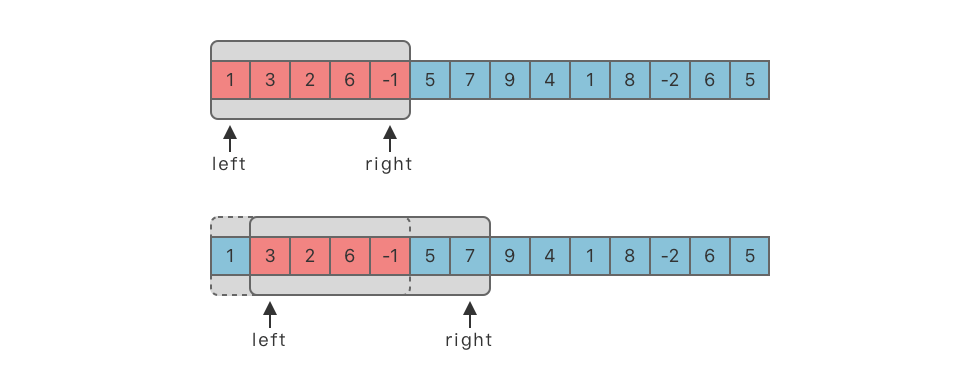
滑动窗口算法（Sliding Window）：在数组 / 字符串上维护一个固定或可变长度的窗口，通过滑动和缩放窗口，动态维护区间内的最优解。

滑动：窗口整体向一个方向移动，通常是向右。
缩放：窗口长度可变时，可以通过移动左指针缩小窗口，或移动右指针扩大窗口。

滑动窗口本质上是双指针（快慢指针）的一种应用，可以理解为用两个指针维护一个区间，动态调整区间范围以满足题目要求。

2. 滑动窗口的应用场景

滑动窗口常用于查找满足某些条件的连续子区间，能将嵌套循环优化为单循环，大幅降低时间复杂度。常见题型包括：

固定长度窗口：窗口大小固定，通常用于统计或查找长度为 $k$ 的区间性质。
可变长度窗口：窗口大小不固定，常用于查找满足条件的最长/最短区间。

下面分别介绍这两类滑动窗口的应用。

3. 固定长度滑动窗口

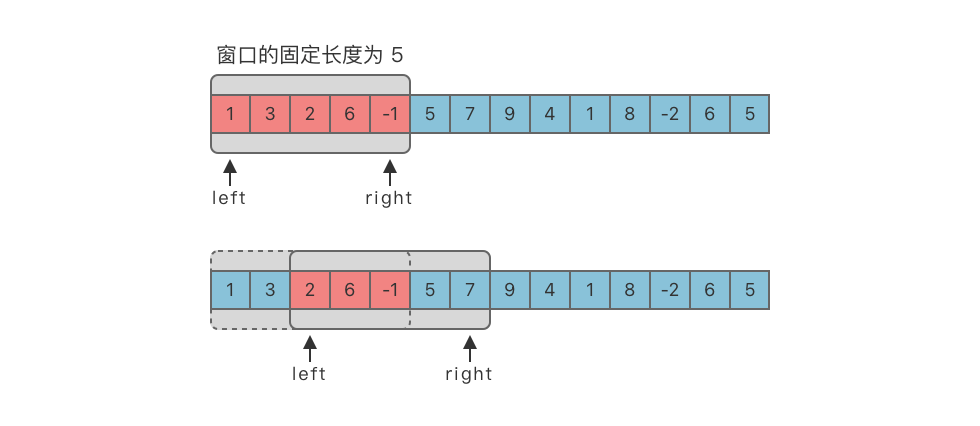
固定长度滑动窗口算法（Fixed Length Sliding Window）：在数组 / 字符串上维护一个长度固定的窗口，通过不断向右滑动窗口，实时更新窗口内的数据，并根据题目要求动态维护最优解。

3.1 固定长度滑动窗口算法步骤

假设窗口大小为 $window\_size$ ，步骤如下：

定义两个指针 $left$ 和 $right$ ，初始都指向序列起始位置（ $left = 0, right = 0$ ），区间 $[left, right]$ 表示当前窗口。
不断右移 $right$ ，将元素加入窗口（如 window.append(nums[right])）。
当窗口长度达到 $window\_size$ $w in d o w_s i ze$ （即 right - left + 1 >= window_size）时：
- 判断窗口内元素是否满足题目要求，若满足则更新答案。
- 右移 $left$ （left += 1），保持窗口长度不变。
重复上述过程，直到 $right$ 遍历完整个数组。

3.2 固定长度滑动窗口代码模板

left = 0  # 窗口左边界
right = 0  # 窗口右边界

while right < len(nums):
    # 将当前元素加入窗口
    window.append(nums[right])
    
    # 判断当前窗口长度是否达到 window_size
    if right - left + 1 >= window_size:
        # 在窗口长度达到要求时，进行答案的统计或更新
        # ... 这里根据题目需求维护/更新答案
        
        # 移除窗口最左侧元素，窗口向右滑动
        window.popleft()  
        left += 1  # 左指针右移，缩小窗口长度，保持窗口长度为 window_size
    
    # 右指针右移，扩大窗口
    right += 1

下面我们通过具体例题，详细说明如何利用固定长度滑动窗口方法高效解决相关问题。

3.3 经典例题：大小为 K 且平均值大于等于阈值的子数组数目

3.3.1 题目链接

1343. 大小为 K 且平均值大于等于阈值的子数组数目 - 力扣（LeetCode）

3.3.2 题目大意

描述：给定一个整数数组 $arr$ 和两个整数 $k$ 和 $threshold$ 。

要求：返回长度为 $k$ 且平均值大于等于 $threshold$ 的子数组数目。

说明：

$1 \le arr.length \le 10^5$ 。
$1 \le arr[i] \le 10^4$ 。
$1 \le k \le arr.length$ 。
$0 \le threshold \le 10^4$ 。

示例：

示例 1：

输入：arr = [2,2,2,2,5,5,5,8], k = 3, threshold = 4
输出：3
解释：子数组 [2,5,5],[5,5,5] 和 [5,5,8] 的平均值分别为 4，5 和 6 。其他长度为 3 的子数组的平均值都小于 4 （threshold 的值)。

示例 2：

输入：arr = [11,13,17,23,29,31,7,5,2,3], k = 3, threshold = 5
输出：6
解释：前 6 个长度为 3 的子数组平均值都大于 5 。注意平均值不是整数。

3.3.3 解题思路

思路 1：滑动窗口（固定长度）

本题是典型的定长滑动窗口问题，窗口大小为 $k$ 。具体做法如下：

用 $window\_sum$ 维护当前窗口内元素和， $ans$ 统计满足条件的子数组个数。
使用两个指针 $left$ 、 $right$ ，初始都为 $0$ 。
每次将 $arr[right]$ 加入 $window\_sum$ ， $right$ 右移。
当窗口长度达到 $k$ （即 right - left + 1 >= k）时，判断窗口平均值是否大于等于 $threshold$ ，满足则 $ans + 1$ 。
然后将 $arr[left]$ 移出窗口， $left$ 右移，保证窗口长度始终为 $k$ 。
重复上述过程直到遍历完整个数组，最后返回 $ans$ 。

思路 1：代码

class Solution:
def numOfSubarrays(self, arr: List[int], k: int, threshold: int) -> int:
left = 0 # 窗口左边界
right = 0 # 窗口右边界
window_sum = 0 # 当前窗口内元素的和
ans = 0 # 满足条件的子数组个数

    while right < len(arr):
        window_sum += arr[right]  # 将右边界元素加入窗口和

        # 当窗口长度达到k时，判断是否满足条件
        if right - left + 1 >= k:
            # 判断当前窗口的平均值是否大于等于 threshold
            if window_sum >= k * threshold:
                ans += 1  # 满足条件，计数加一
            window_sum -= arr[left]  # 移除左边界元素，准备滑动窗口
            left += 1  # 左边界右移

        right += 1  # 右边界右移，扩大窗口

    return ans  # 返回满足条件的子数组个数

思路 1：复杂度分析

时间复杂度： $O(n)$ 。
空间复杂度： $O(1)$ 。

4. 不定长度滑动窗口

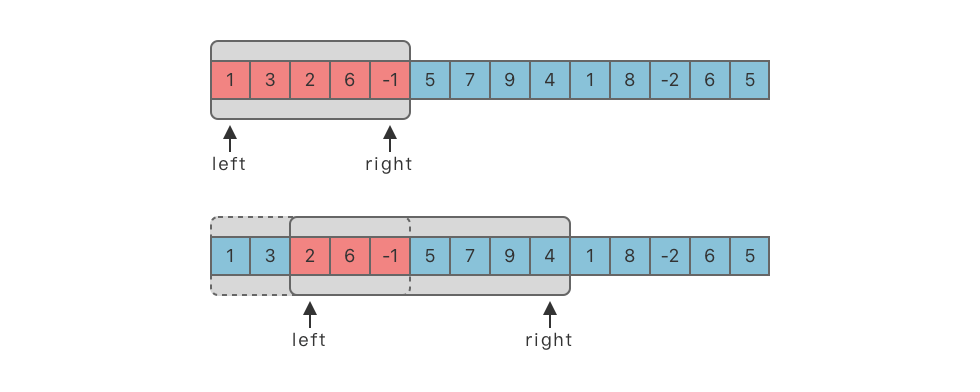
不定长滑动窗口（Sliding Window）：在数组 / 字符串上用两个指针动态维护一个可变长度的窗口，通过左右移动指针灵活调整窗口范围，实时维护最优解。

4.1 不定长度滑动窗口算法步骤

定义左右指针 $left$ 、 $right$ ，初始都为 $0$ ，区间 $[left, right]$ 表示当前窗口。
将 $s[right]$ 加入窗口（如 window.add(s[right])），然后 $right += 1$ ，扩大窗口。
当窗口不满足条件时，不断移除 $s[left]$ （如 window.popleft()），并 $left += 1$ ，缩小窗口，直到重新满足条件。
重复上述过程，直到 $right$ 遍历完整个序列。

4.2 不定长度滑动窗口代码模板

# 初始化左右指针，均指向数组起始位置
left = 0
right = 0

# 主循环，右指针遍历整个数组
while right < len(nums):
    # 将当前右指针指向的元素加入窗口
    window.append(nums[right])
    
    # 当窗口不满足题目要求时，缩小窗口（移动左指针）
    while 窗口需要缩小:
        # 此处可根据题意维护/更新答案
        window.popleft()  # 移除左边界元素
        left += 1         # 左指针右移，缩小窗口
    
    # 此处可根据题意维护/更新答案（如记录最大/最小窗口等）
    
    # 右指针右移，扩大窗口
    right += 1

4.3 经典例题：无重复字符的最长子串

4.3.1 题目链接

3. 无重复字符的最长子串 - 力扣（LeetCode）

4.3.2 题目大意

描述：给定一个字符串 $s$ 。

要求：找出其中不含有重复字符的最长子串的长度。

说明：

$0 \le s.length \le 5 * 10^4$ 。
$s$ 由英文字母、数字、符号和空格组成。

示例：

示例 1：

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2：

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

4.3.3 解题思路

思路 1：滑动窗口（不定长度）

使用滑动窗口（哈希表 $window$ 记录窗口内每个字符出现的次数）来维护一个不含重复字符的子串。

初始化两个指针 $left$ 和 $right$ ，分别作为滑动窗口的左右边界，初始都为 $0$ 。
右指针 $right$ 向右移动，每次将 $s[right]$ 加入 window，并统计其出现次数。
若当前字符 $s[right]$ 在窗口中的出现次数大于 $1$ （即 $window[s[right]] > 1$ ），说明出现重复字符。此时不断右移左指针 $left$ ，并相应减少 $window[s[left]]$ 的计数，直到窗口内 $s[right]$ 只出现一次，保证窗口内无重复字符。
每次窗口合法（无重复字符）时，更新最长子串长度的答案。
重复上述过程，直到 $right$ 遍历完整个字符串。
最终返回无重复字符的最长子串长度。

思路 1：代码

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        left = 0  # 滑动窗口左边界
        right = 0  # 滑动窗口右边界
        window = dict()  # 记录窗口内每个字符出现的次数
        ans = 0  # 记录最长无重复子串的长度

        while right < len(s):
            # 将当前字符加入窗口，统计出现次数
            if s[right] not in window:
                window[s[right]] = 1
            else:
                window[s[right]] += 1

            # 如果当前字符出现次数大于1，说明有重复，需要收缩左边界
            while window[s[right]] > 1:
                window[s[left]] -= 1  # 左边界字符出现次数减少
                left += 1  # 左边界右移，缩小窗口

            # 更新最长无重复子串的长度
            ans = max(ans, right - left + 1)
            right += 1  # 右边界右移，扩大窗口

        return ans  # 返回结果

思路 1：复杂度分析

时间复杂度： $O(n)$ 。
空间复杂度： $O(| \sum |)$ 。其中 $\sum$ 表示字符集， $| \sum |$ 表示字符集的大小。

5. 总结

滑动窗口算法高效解决数组或字符串的连续区间问题。

固定长度窗口：窗口大小固定，常用于统计定长子区间的和、均值等。
不定长度窗口：窗口大小可变，适合查找最长/最短满足条件的子区间，如最长无重复子串。

滑动窗口通过动态调整左右边界，避免重复遍历，将时间复杂度从 $O(n^2)$ 降至 $O(n)$ 。

使用时需注意：

窗口的起始位置
何时扩展或收缩窗口
如何及时更新答案
边界情况处理

熟练掌握滑动窗口，可高效应对各类区间类问题。

1.16 数组滑动窗口

1.16 数组滑动窗口

1. 滑动窗口算法简介

2. 滑动窗口的应用场景

3. 固定长度滑动窗口

3.1 固定长度滑动窗口算法步骤

3.2 固定长度滑动窗口代码模板

3.3 经典例题：大小为 K 且平均值大于等于阈值的子数组数目

3.3.1 题目链接

3.3.2 题目大意

3.3.3 解题思路

思路 1：滑动窗口（固定长度）

思路 1：代码

思路 1：复杂度分析

4. 不定长度滑动窗口

4.1 不定长度滑动窗口算法步骤

4.2 不定长度滑动窗口代码模板

4.3 经典例题：无重复字符的最长子串

4.3.1 题目链接

4.3.2 题目大意

4.3.3 解题思路

思路 1：滑动窗口（不定长度）

思路 1：代码

思路 1：复杂度分析

5. 总结

练习题目

参考资料