跳至主要內容

2.1 链表基础

ITCharge大约 12 分钟

2.1 链表基础

---

1. 链表简介

1.1 链表定义

链表（Linked List）：一种线性表数据结构，通过一组任意（可连续或不连续）的存储单元，存储同类型数据。

简而言之，链表 是线性表的链式存储实现。

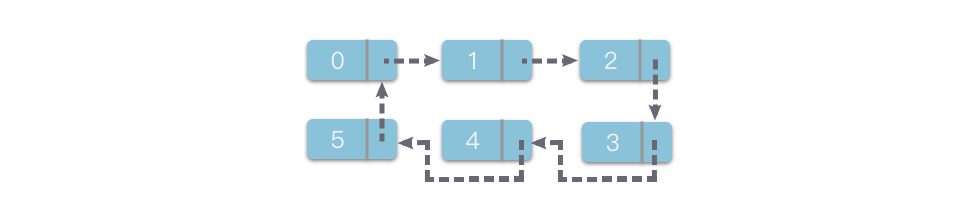
以单链表为例，其结构如下图：

链表
链表

如上图所示，链表通过指针将一组任意的存储单元串联起来。每个数据元素及其所在的存储单元构成一个「链节点」。为了将所有节点连接成链，每个链节点除了存放数据元素本身，还需要额外存储一个指向其直接后继节点的指针，称为「后继指针 nextnext」。

在链表结构中，数据元素之间的逻辑顺序由指针维护。虽然逻辑上相邻的数据元素在物理内存中可以相邻，也可以完全不相邻，因此链表在物理存储上的分布是非连续、随机的。

链表的优缺点如下：

  • 优点：链表无需预先分配存储空间，按需动态申请，能够有效避免空间浪费；在插入、删除等操作上，链表通常比数组更高效，尤其是在需要频繁修改数据结构时表现突出。

  • 缺点：链表除了存储数据本身外，还需额外存储指针信息，因此整体空间开销大于数组；同时，链表不支持随机访问，查找元素时需要从头遍历，效率较低。

下面介绍除单链表外的其他链表类型。

1.2 双向链表

双向链表（Doubly Linked List）：链表的一种，也称为双链表。每个节点包含两个指针，分别指向其直接前驱和直接后继节点。

  • 双向链表的特点：可以从任意节点高效地访问其前驱和后继节点，支持双向遍历，插入和删除操作更加灵活。
双向链表
双向链表

1.3 循环链表

循环链表（Circular Linked List）：一种特殊的链表结构，其最后一个节点的指针指向头节点，从而使整个链表首尾相连，形成一个闭环。

  • 循环链表的特点：无论从哪个节点出发，都可以遍历到链表中的任意节点，实现了节点间的循环访问。
循环链表
循环链表

下面我们将以最基础的「单链表」为例，详细讲解链表的基本操作。

2. 链表的基本操作

在数据结构中，常见的基本操作包括增、删、改、查四类，链表的操作同样主要围绕这四个方面展开。下面我们详细介绍链表的基本操作。

2.1 链表的结构定义

链表由若干链节点通过 nextnext 指针依次连接而成。通常我们会先定义一个简单的「链节点类」，再基于此实现完整的「链表类」。

  • 链节点类（ListNode）：包含成员变量 valval（存储数据元素的值）和 nextnext（指向下一个节点的指针）。

  • 链表类（LinkedList）：包含一个链节点变量 headhead，用于表示链表的头节点。

创建空链表时，只需将头节点 headhead 设为「空指针」。在 Python 中可用 NoneNone 表示，其他语言中常用 NULLNULL、nilnil、00 等。

链节点与链表结构的代码实现如下：

# 链节点类
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val      # 节点的值
        self.next = next    # 指向下一个节点

class LinkedList:
    def __init__(self):
        self.head = None    # 链表头指针，初始为 None

2.2 创建链表

创建链表：根据给定的线性表数据，依次生成链表节点，并将它们顺序连接起来，构成完整的链表。

具体步骤如下：

  1. 取出线性表的第 11 个元素，创建链表头节点。
  2. 依次遍历剩余元素，每获取一个数据元素，就新建一个节点，并将其连接到当前链表的尾部。
  3. 所有元素插入完成后，返回头节点。

创建链表 的实现代码如下：

# 根据 data 列表初始化一个新链表
def create(self, data):
    if not data:
        # 如果输入数据为空，直接返回，不创建链表
        return
    # 创建头节点，并将 head 指向头节点
    self.head = ListNode(data[0])
    cur = self.head  # cur 用于指向当前链表的尾节点
    # 依次遍历 data 中剩余的元素，逐个创建新节点并连接到链表尾部
    for i in range(1, len(data)):
        node = ListNode(data[i])  # 创建新节点
        cur.next = node           # 将新节点连接到当前尾节点
        cur = cur.next            # cur 指向新的尾节点，准备连接下一个节点

「创建链表」的操作需要遍历所有数据元素，时间复杂度为 O(n)O(n)，其中 nn 为线性表的长度。

2.3 链表长度

链表长度：通过一个指针变量 curcur 沿着链表的 nextnext 指针逐个遍历节点，并用计数器 countcount 统计节点数量，最终得到链表长度。

具体步骤如下：

  1. 令指针 curcur 指向链表头节点（第 11 个节点）。
  2. 沿着 nextnext 指针遍历链表，每访问一个节点，计数器 countcount 加 11。
  3. 当 curcur 变为 NoneNone（即遍历到链表末尾）时，遍历结束，此时 countcount 即为链表长度，返回该值。

「求链表长度」 的实现代码如下：

# 获取线性链表长度
def length(self):
    count = 0                # 初始化计数器，记录节点个数
    cur = self.head          # 从链表头节点开始遍历
    while cur:               # 只要当前节点不为 None，就继续遍历
        count += 1           # 每遍历到一个节点，计数器加 1
        cur = cur.next       # 指针后移，指向下一个节点
    return count             # 返回计数器的值，即链表长度

「求链表长度」的操作需要遍历链表的所有节点，操作次数为 nn，因此时间复杂度为 O(n)O(n)，其中 nn 为链表长度。

2.4 查找节点

链表中查找值为 valval 的节点：从头节点 headhead 开始，依次遍历链表，查找值等于 valval 的节点。如果找到，返回该节点；否则返回 NoneNone。

具体步骤如下：

  1. 定义指针变量 curcur，初始指向链表的头节点。
  2. 沿着链表的 nextnext 指针依次遍历每个节点：
    • 如果当前节点 curcur 的值等于 valval，则查找成功，返回该节点。
    • 否则，curcur 指向下一个节点，继续查找。
  3. 如果遍历完整个链表仍未找到，说明链表中不存在值为 valval 的节点，返回 NoneNone。

「链表中查找值为 valval 的节点」 的实现代码如下：

# 链表中查找值为 val 的节点
def find(self, val):
    cur = self.head  # 从链表头节点开始遍历
    while cur:  # 只要当前节点不为 None，就继续遍历
        if val == cur.val:  # 如果当前节点的值等于目标值，查找成功
            return cur      # 返回当前节点
        cur = cur.next      # 指针后移，指向下一个节点

    # 遍历完整个链表都没有找到目标值，返回 None
    return None

「链表中查找值为 valval 的节点」需要遍历链表的所有节点，因此其时间复杂度为 O(n)O(n)，其中 nn 表示链表的长度。

2.5 插入节点

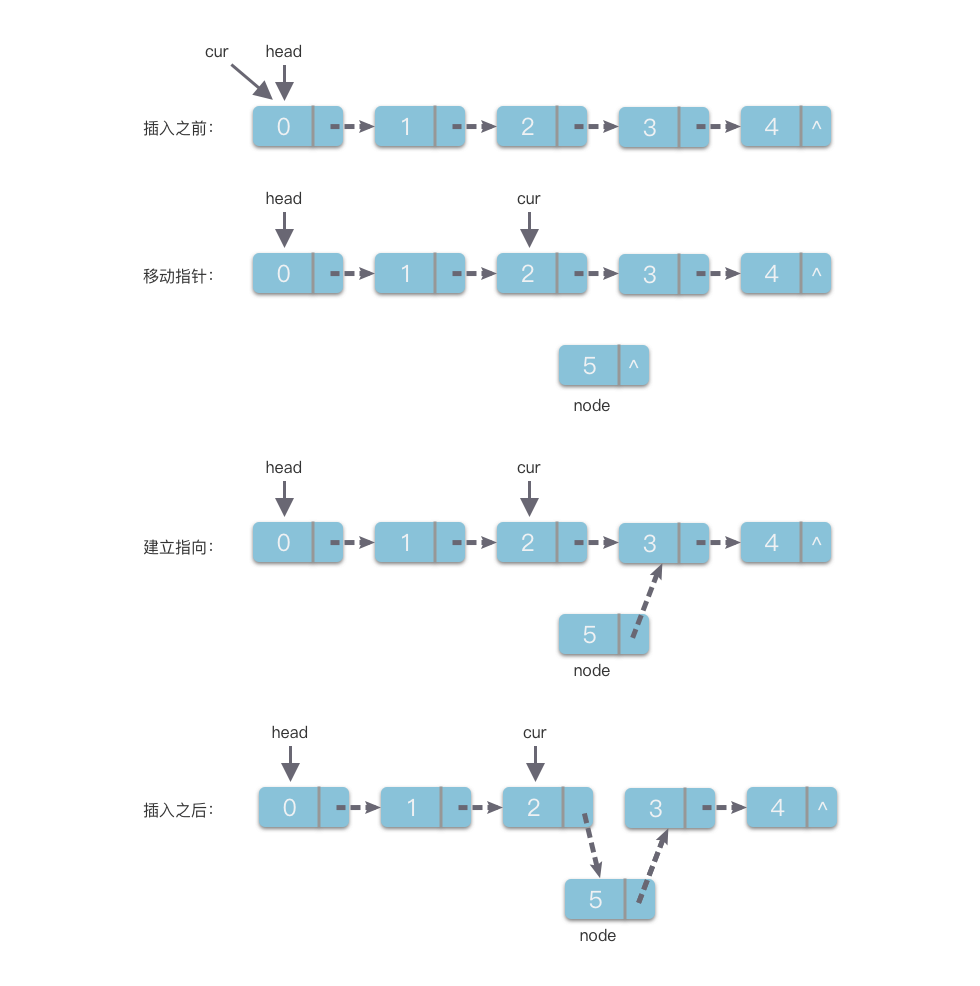
  • 插入节点：在链表的第 ii 个位置前插入一个值为 valval 的新节点。

具体步骤如下：

  1. 定义指针变量 curcur，初始指向链表头节点，同时定义计数器 countcount，初始值为 00。
  2. 沿着链表的 nextnext 指针遍历，curcur 每指向一个节点，countcount 加 11。
  3. 当 countcount 等于 index−1index - 1 时，curcur 正好指向第 index−1index - 1 个节点（即新节点的前驱节点），此时停止遍历。
  4. 创建一个新节点 nodenode，其值为 valval。
  5. 将 node.nextnode.next 指向 cur.nextcur.next，即新节点的后继为原本的第 indexindex 个节点。
  6. 将 cur.nextcur.next 指向 nodenode，完成插入操作。

注意：如果 index=1index = 1，即在头节点前插入，需要特殊处理（如使用虚拟头节点或单独判断）。

插入节点
插入节点

「插入节点」 的实现代码如下：

# 插入节点
def insertInside(self, index, val):
    # 头部插入（index == 1）
    if index == 1:
        node = ListNode(val)
        node.next = self.head
        self.head = node
        return

    count = 0
    cur = self.head
    # 遍历链表，找到第 index - 1 个节点（即新节点的前驱节点）
    while cur and count < index - 1:
        cur = cur.next
        count += 1

    # 如果遍历到链表末尾还没找到前驱节点，说明 index 越界，插入失败
    if not cur:
        return 'Error'

    node = ListNode(val)
    # 尾部插入（index 指向最后一个节点的下一个位置）
    if cur.next is None:
        cur.next = node
    else:
        node.next = cur.next
        cur.next = node

「插入节点」操作需要将指针 curcur 从链表头部遍历到第 ii 个节点的前一个位置，平均时间复杂度为 O(n)O(n)，因此整体的时间复杂度为 O(n)O(n)。

2.6 改变节点

将链表中第 ii 个节点的值修改为 valval：只需遍历到第 ii 个节点，然后直接修改该节点的值。具体步骤如下：

  1. 定义指针变量 curcur 指向链表头节点，并设置计数器 countcount，初始为 00。
  2. 沿着 nextnext 指针遍历链表，每遍历一个节点，countcount 加 11。
  3. 当 countcount 等于 indexindex 时，curcur 正好指向第 ii 个节点，停止遍历。
  4. 直接将 curcur 的值设为 valval。

「将链表中第 ii 个节点的值修改为 valval」 的实现代码如下：

# 改变元素：将链表中第 i 个元素值改为 val
def change(self, index, val):
    # 初始化计数器 count 和指针 cur，cur 指向链表头节点
    count = 0
    cur = self.head
    # 遍历链表，直到找到第 index 个节点
    while cur and count < index:
        count += 1
        cur = cur.next
        
    # 如果 cur 为空，说明 index 越界，返回错误
    if not cur:
        return 'Error'

    # 修改第 index 个节点的值为 val
    cur.val = val

要将链表中第 ii 个节点的值修改为 valval，需要从链表头节点出发，遍历到第 ii 个节点，然后进行赋值操作。由于遍历链表的时间复杂度为 O(n)O(n)，因此该操作的整体时间复杂度为 O(n)O(n)。

2.7 删除元素

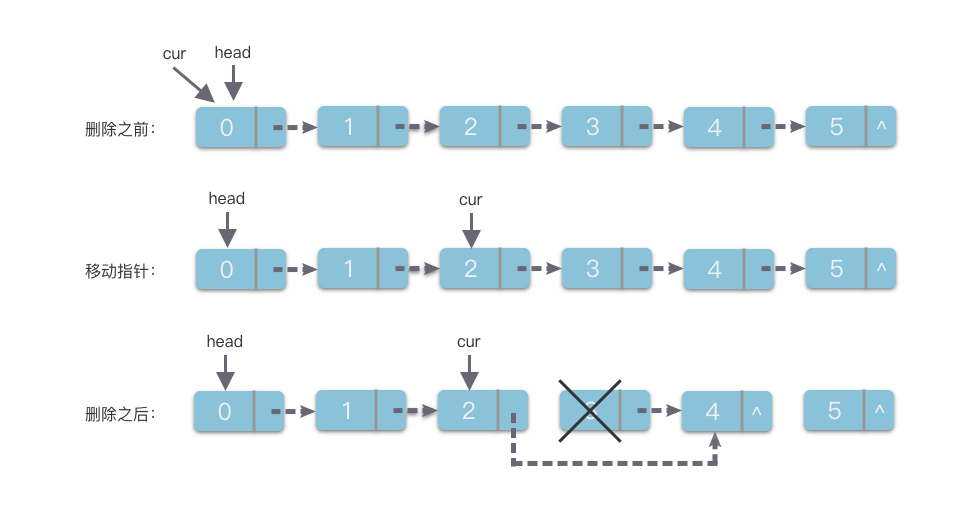
删除元素：删除链表中第 ii 个节点。

具体步骤如下：

  1. 使用指针变量 curcur 遍历至第 i−1i - 1 个节点（即待删除节点的前驱）。
  2. 将 curcur 的 nextnext 指针指向第 ii 个节点的下一个节点，从而跳过并移除第 ii 个节点。
删除元素
删除元素

「删除元素」 的实现代码如下：

# 链表删除元素
def removeInside(self, index):
    # 初始化计数器 count 和指针 cur，cur 指向链表头节点
    count = 0
    cur = self.head

    # 遍历链表，cur 移动到第 index - 1 个节点（即待删除节点的前驱）
    while cur.next and count < index - 1:
        count += 1
        cur = cur.next

    # 如果 cur 为空，说明 index 越界，返回错误
    if not cur:
        return 'Error'

    # del_node 指向待删除的节点
    del_node = cur.next
    # 将 cur 的 next 指针指向 del_node 的下一个节点，实现删除
    cur.next = del_node.next

「删除元素」操作需要将指针 curcur 从链表头节点遍历至第 ii 个节点的前一个节点，因此其时间复杂度为 O(n)O(n)。

3. 总结

3.1 链表特点

链表是一种链式存储的线性表数据结构，具有以下核心特征：

  • 存储方式：通过指针连接任意存储单元，物理存储非连续
  • 节点结构：每个节点包含数据域和指针域
  • 访问方式：只能顺序访问，不支持随机访问

3.2 链表类型

类型特点适用场景
单链表每个节点只有一个后继指针基础链表操作
双向链表每个节点有前驱和后继指针需要双向遍历
循环链表尾节点指向头节点形成环循环访问场景

3.3 基本操作复杂度

操作时间复杂度空间复杂度说明
查找O(n)O(n)O(1)O(1)需要遍历到目标位置
插入O(n)O(n)O(1)O(1)找到插入位置后操作简单
删除O(n)O(n)O(1)O(1)找到删除位置后操作简单
修改O(n)O(n)O(1)O(1)需要遍历到目标位置

3.4 链表 vs 数组

特性链表数组
存储方式链式存储，非连续顺序存储，连续
随机访问不支持，O(n)O(n)支持，O(1)O(1)
插入删除高效，O(1)O(1)（已知位置）需要移动元素，O(n)O(n)
空间开销额外指针开销无额外开销
内存分配动态分配静态分配

3.5 应用场景

  • 频繁插入删除：链表在插入删除操作上比数组更高效
  • 动态内存管理：适合内存大小不确定的场景
  • 实现其他数据结构：栈、队列、哈希表等的基础
  • 算法优化：某些算法中链表结构能提供更好的性能

练习题目

参考资料

本站总访问量  次 | 您是本站第  位访问者
Copyright © 2025 ITCharge