3.4 优先队列

---

1. 优先队列简介

优先队列（Priority Queue）：是一种为每个元素分配优先级的特殊队列结构。每次访问或移除元素时，总是优先处理优先级最高的元素。

优先队列与普通队列的核心区别在于 出队顺序：

• 普通队列按照「先进先出（First In, First Out）」原则，元素按入队顺序依次出队。
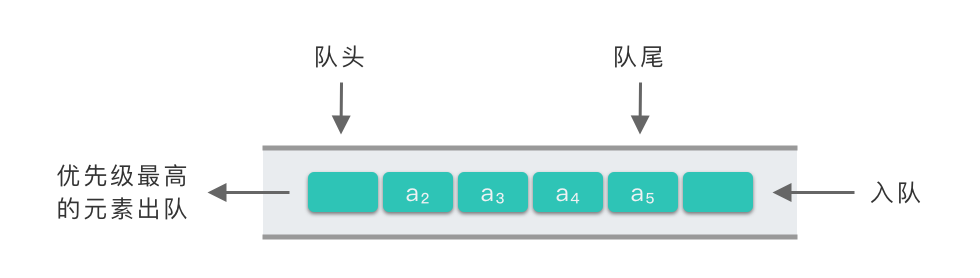
• 优先队列则根据元素的优先级决定出队顺序，优先级高的元素先出队，优先级低的元素后出队，遵循 「优先级高者先出」 的规则，与入队顺序无关。

下图展示了优先队列的结构示意：

优先队列

优先队列在实际开发和算法设计中有着广泛的应用，常见场景包括：

• 数据压缩：如赫夫曼编码算法中，频率最低的节点优先合并。
• 最短路径搜索：如 Dijkstra 算法，优先扩展当前距离最小的节点。
• 最小生成树构建：如 Prim 算法，优先选择权值最小的边。
• 任务调度：根据任务优先级动态分配执行顺序。
• 事件驱动仿真：如排队系统，优先处理最早到达或优先级最高的事件。
• Top-K 问题：如查找第 k 大（小）元素、实时维护前 K 个高频元素等。

主流编程语言均内置了优先队列相关的数据结构。例如 Java 的 PriorityQueue，C++ 的 priority_queue，Python 可通过 heapq 模块实现优先队列。接下来将详细介绍优先队列的实现方式。

2. 优先队列的实现方式

优先队列的基本操作与普通队列类似，主要包括 「入队」 和 「出队」，但在出队时会优先移除优先级最高的元素。

优先队列的实现方式主要有三种：数组（顺序存储）、链表（链式存储） 和 二叉堆结构。其中，最常用且高效的是基于二叉堆的实现。下面简要对比三种方案：

• 数组（顺序存储）：入队时直接将元素插入数组末尾，时间复杂度为 $O(1)$；出队时需遍历整个数组以找到优先级最高的元素并删除，时间复杂度为 $O(n)$。
• 链表（链式存储）：链表内元素按优先级有序排列，入队时需找到合适插入位置，时间复杂度为 $O(n)$；出队时直接移除链表头节点，时间复杂度为 $O(1)$。
• 二叉堆结构：通过二叉堆维护优先级顺序，入队操作（插入新元素）和出队操作（弹出优先级最高元素）均为 $O(\log n)$，效率较高。

三种实现方式的时间复杂度对比如下：

实现方式	入队操作	出队操作（取优先级最高元素）
二叉堆	$O(\log n)$	$O(\log n)$
数组	$O(1)$	$O(n)$
链表	$O(n)$	$O(1)$

综上，二叉堆是实现优先队列的主流高效方案。接下来将详细介绍基于二叉堆的优先队列实现。

3. 二叉堆实现的优先队列

3.1 二叉堆的定义

二叉堆是一种完全二叉树，分为两类：

• 大顶堆：每个节点值 ≥ 子节点值
• 小顶堆：每个节点值 ≤ 子节点值

3.2 二叉堆的基本操作

二叉堆的核心操作有两个：

• 堆调整（heapAdjust）：从某个节点出发，自上而下比较并交换，使以该节点为根的子树满足堆性质（如大顶堆则父节点 ≥ 子节点），直到整个堆有序。
• 建堆（heapify）：从最后一个非叶子节点开始，依次向前对每个节点执行堆调整，最终将数组整体调整为二叉堆。

3.3 优先队列的基本操作

优先队列主要有两种操作：

• 入队（heappush）：将新元素加到数组末尾，然后从下往上调整，恢复堆结构。
• 出队（heappop）：将堆顶元素与末尾元素交换，弹出末尾元素，再对新堆顶自上而下调整，恢复堆结构。

3.4 手写二叉堆实现优先队列

手写二叉堆实现优先队列，常用方法包括：

• heapAdjust：调整堆结构
• heapify：建堆
• heappush：入队
• heappop：出队
• heapSort：堆排序

class Heapq:
    # 堆调整方法：将以 index 为根的子树调整为大顶堆
    def heapAdjust(self, nums: list, index: int, end: int):
        """
        nums: 堆数组
        index: 当前需要调整的根节点下标
        end: 堆的最后一个元素下标
        """
        left = index * 2 + 1  # 左子节点下标
        right = left + 1      # 右子节点下标
        while left <= end:
            max_index = index  # 假设当前根节点最大
            # 比较左子节点
            if nums[left] > nums[max_index]:
                max_index = left
            # 比较右子节点（注意要先判断是否越界）
            if right <= end and nums[right] > nums[max_index]:
                max_index = right
            if index == max_index:
                # 如果根节点就是最大值，调整结束
                break
            # 交换根节点与最大子节点
            nums[index], nums[max_index] = nums[max_index], nums[index]
            # 继续调整被交换下去的子树
            index = max_index
            left = index * 2 + 1
            right = left + 1

    # 建堆：将数组整体调整为大顶堆
    def heapify(self, nums: list):
        size = len(nums)
        # 从最后一个非叶子节点开始，依次向前调整
        for i in range((size - 2) // 2, -1, -1):
            self.heapAdjust(nums, i, size - 1)

    # 入队操作：插入新元素到堆中
    def heappush(self, nums: list, value):
        """
        nums: 堆数组
        value: 待插入的新元素
        """
        nums.append(value)  # 先将新元素加到末尾
        i = len(nums) - 1   # 新元素下标
        # 自下向上调整，恢复堆结构
        while i > 0:
            parent = (i - 1) // 2  # 父节点下标
            if nums[parent] >= value:
                # 父节点比新元素大，插入到当前位置
                break
            # 父节点下移
            nums[i] = nums[parent]
            i = parent
        nums[i] = value  # 插入到最终位置

    # 出队操作：弹出堆顶元素（最大值）
    def heappop(self, nums: list) -> int:
        """
        nums: 堆数组
        return: 堆顶元素
        """
        size = len(nums)
        if size == 0:
            raise IndexError("heappop from empty heap")
        # 交换堆顶和末尾元素
        nums[0], nums[-1] = nums[-1], nums[0]
        top = nums.pop()  # 弹出最大值
        if size > 1:
            # 重新调整堆
            self.heapAdjust(nums, 0, size - 2)
        return top

    # 堆排序：原地将数组升序排序
    def heapSort(self, nums: list):
        """
        nums: 待排序数组
        return: 升序排序后的数组
        """
        self.heapify(nums)  # 先建堆
        size = len(nums)
        # 依次将堆顶元素（最大值）交换到末尾，缩小堆范围
        for i in range(size - 1, 0, -1):
            nums[0], nums[i] = nums[i], nums[0]  # 堆顶与末尾交换
            self.heapAdjust(nums, 0, i - 1)      # 调整剩余部分为大顶堆
        return nums

3.5 使用 heapq 模块实现优先队列

Python 标准库中的 heapq 模块实现了高效的最小堆（小顶堆），可用于构建优先队列。其核心操作如下：

• heapq.heappush(heap, item)：将元素 item 压入堆 heap 中，保持堆结构。
• heapq.heappop(heap)：弹出并返回堆中的最小元素。

注意事项：

• heapq 默认是小顶堆，即每次弹出的是最小值。
• 若需实现「大顶堆」（每次弹出最大优先级元素），可将优先级取负数存入堆中。
• 为保证当优先级相同时元素的入队顺序，通常可额外存储一个自增索引。

下面是一个基于 heapq 实现的优先队列类，支持自定义优先级，且保证稳定性：

import heapq

class PriorityQueue:
    def __init__(self):
        # 初始化一个空堆和自增索引
        self.queue = []
        self.index = 0

    def push(self, item, priority):
        """
        入队操作，将元素 item 按照优先级 priority 压入堆中。
        为实现大顶堆，优先级取负数；index 保证相同优先级时的稳定性。
        """
        heapq.heappush(self.queue, (-priority, self.index, item))
        self.index += 1

    def pop(self):
        """
        出队操作，弹出并返回优先级最高的元素（大顶堆）。
        """
        if not self.queue:
            raise IndexError("pop from empty priority queue")
        return heapq.heappop(self.queue)[-1]

5. 经典例题：滑动窗口最大值

5.1.1 题目链接

• 239. 滑动窗口最大值 - 力扣（LeetCode）

5.1.2 题目大意

描述：给定一个整数数组 $nums$，再给定一个整数 $k$，表示为大小为 $k$ 的滑动窗口从数组的最左侧移动到数组的最右侧。我们只能看到滑动窗口内的 $k$ 个数字，滑动窗口每次只能向右移动一位。

要求：返回滑动窗口中的最大值。

说明：

• $1 \le nums.length \le 10^5$。
• $-10^4 \le nums[i] \le 10^4$。
• $1 \le k \le nums.length$。

示例：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

 
输入：nums = [1], k = 1
输出：[1]

5.1.3 解题思路

如果采用暴力解法，需要用两重循环遍历每个滑动窗口，时间复杂度为 $O(n \times k)$，在本题数据范围下会超时。

可以利用优先队列（堆）高效求解：

思路 1：优先队列

1. 首先，将前 $k$ 个元素以 (值, 索引) 形式加入优先队列（大顶堆），以值为优先级。
2. 从第 $k$ 个元素开始，依次将当前元素及其索引压入堆中。
3. 每次插入后，检查堆顶元素的索引是否已滑出窗口（即 $q[0][1] \le i - k$），若是则不断弹出堆顶，直到堆顶索引在窗口范围内。
4. 此时堆顶元素即为当前窗口最大值，将其加入结果数组。
5. 重复上述过程，直到遍历完整个数组，最后返回结果数组。

思路 1：代码

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        size = len(nums)
        q = [(-nums[i], i) for i in range(k)]
        heapq.heapify(q)
        res = [-q[0][0]]

        for i in range(k, size):
            heapq.heappush(q, (-nums[i], i))
            while q[0][1] <= i - k:
                heapq.heappop(q)
            res.append(-q[0][0])
        return res

思路 1：复杂度分析

• 时间复杂度：$O(n \times \log n)$。
• 空间复杂度：$O(k)$。

练习题目

• 0215. 数组中的第K个最大元素

• 0347. 前 K 个高频元素

• 0451. 根据字符出现频率排序

• 优先队列题目列表

参考资料

• 【博文】浅入浅出数据结构（15）—— 优先队列（堆） - NSpt - 博客园
• 【博文】堆（Heap）和优先队列（Priority Queue） - 简书
• 【博文】漫画：什么是优先队列？- 吴师兄学编程
• 【博文】Python3，手写一个堆及其简易功能，并实现优先队列，最小堆任务调度等 - pythonstrat 的博客
• 【文档】实现一个优先级队列 - python3-cookbook 3.0.0 文档
• 【文档】heapq - 堆队列算法 - Python 3.10.1 文档
• 【题解】239. 滑动窗口最大值 （优先队列&单调栈） - 滑动窗口最大值 - 力扣