3.6 哈希表

ITCharge大约 10 分钟

3.6 哈希表

---

1. 哈希表简介

哈希表（Hash Table），又称散列表，是一种能通过关键码（Key）直接访问数据的结构。
哈希表利用「键 $key$ 」和「哈希函数 $Hash(key)$ 」将关键码映射到表中的某个位置，从而实现高效的查找和存储。这个映射过程由「哈希函数（散列函数）」完成，存储数据的数组称为「哈希表（散列表）」。

哈希表的核心思想是：通过哈希函数将键 $key$ 映射到表的某个区块，实现高效的数据插入与查找。其基本操作流程如下：

插入关键码：利用哈希函数计算关键字应存放的区块索引，然后将数据存入该区块。
查找关键码：用相同的哈希函数定位区块，再在该区块中查找目标数据。

如下图所示为哈希表的原理示意：

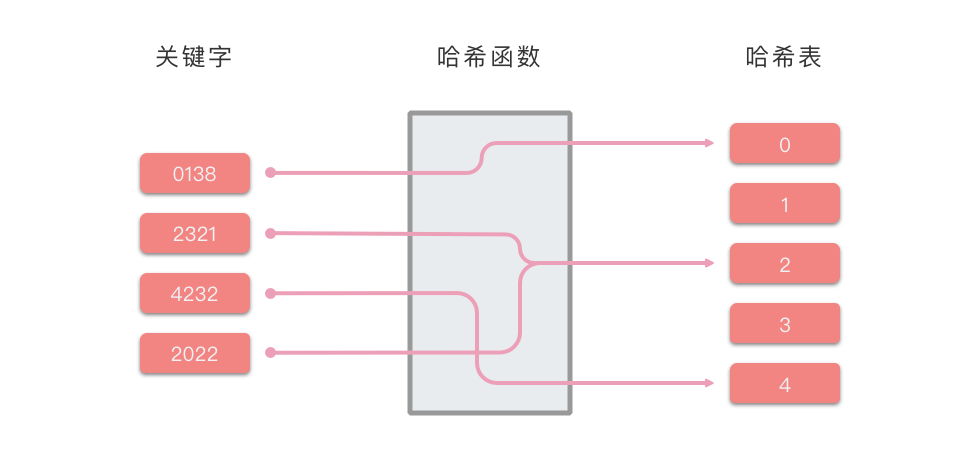
以图中为例，假设哈希函数为 $Hash(key) = key // 1000$ （ $//$ 表示整除），则哈希表的插入和查找过程如下：

插入：如 $0138$ ，通过 $Hash(0138) = 0$ ，应存入第 $0$ 区块。
查找：
- 查找 $2321$ ， $Hash(2321) = 2$ ，在第 $2$ 区块中找到 $2321$ 。
- 查找 $3214$ ， $Hash(3214) = 3$ ，在第 $3$ 区块未找到，说明 $3214$ 不在哈希表中。

哈希表在实际生活中也有广泛应用，例如「查字典」：

查找 「赞」 这个字时，我们根据拼音索引 zan 查到页码 $599$ ，然后翻到第 $599$ 页即可查看解释。

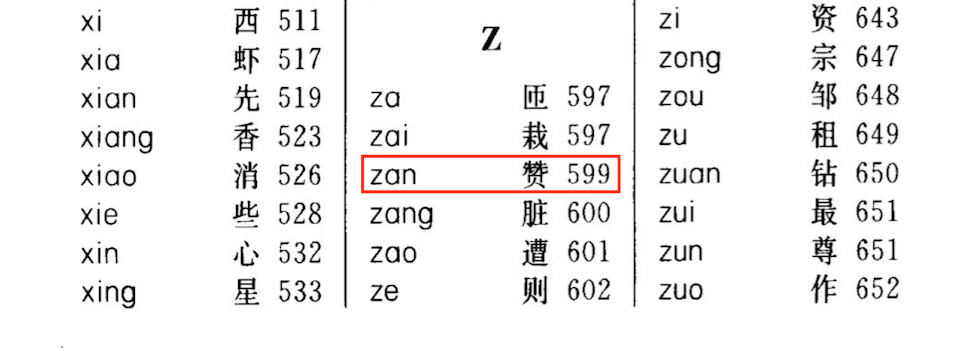
在这个例子中：

存放拼音与页码的表，相当于 哈希表。
「赞」 的拼音 zan，相当于哈希表的 关键字 $key$ 。
通过拼音查页码的过程，相当于 哈希函数 $Hash(key)$ 的作用。
查到的页码 $599$ ，相当于哈希表中的 哈希地址 $value$ 。

2. 哈希函数

哈希函数（Hash Function）：是一种将元素的关键字映射为哈希表存储位置的函数。

哈希函数是哈希表设计的核心。一个优秀的哈希函数通常应具备以下特点：

计算简单高效，便于实现；
能将关键字均匀分布到哈希表的各个位置，减少冲突；
输出哈希值为固定长度；
如果 $Hash(key1) \ne Hash(key2)$ ，则 $key1$ 和 $key2$ 必然不同；
如果 $Hash(key1) = Hash(key2)$ ，则 $key1$ 和 $key2$ 可能相同，也可能不同（即可能发生哈希冲突）。

在实际应用中，关键字类型可能为数字、字符串、浮点数、大整数，甚至多种类型的组合。通常会先将各种类型的关键字转换为整数，再通过哈希函数映射到哈希表中。

针对整数类型关键字，常见的哈希函数设计方法包括：直接定址法、除留余数法、平方取中法、基数转换法、数字分析法、折叠法、随机数法、乘积法、点积法等。下面介绍几种常用方法：

2.1 直接定址法

直接定址法：直接取关键字本身或其线性函数作为哈希地址，即 $Hash(key) = key$ 或 $Hash(key) = a \times key + b$ ，其中 $a$ 、 $b$ 为常数。

该方法计算极为简单，且不会产生冲突，适用于关键字分布连续的场景。如果关键字分布稀疏，则会造成空间浪费。

例如，统计 $1 \sim 100$ 岁人口，年龄为关键字，哈希函数取关键字本身：

年龄	1	2	3	...	25	26	27	...	100
人数	3000	2000	5000	...	1050	...	...	...	...

假如想要查询 $25$ 岁人数，直接访问第 $25$ 项即可。

2.2 除留余数法

除留余数法：设哈希表长度为 $m$ ，选取不大于 $m$ 的质数 $p$ ，用 $Hash(key) = key \mod p$ 计算哈希地址。

这是最常用的哈希函数之一。关键在于 $p$ 的选择，通常取质数或与 $m$ 接近的数，以减少冲突。

例如，将 $[432, 5, 128, 193, 92, 111, 88]$ 存入长度为 $11$ 的哈希表，哈希地址如下：

索引	00	01	02	03	04	05	06	07	08	09	10
数据	88	111		432	92	5	193		128

2.3 平方取中法

平方取中法：先对关键字平方，再取中间若干位作为哈希地址。例如 $Hash(key) = (key \times key) // 100 \mod 1000$ ，即先平方，去掉末尾两位，再取中间三位。

该方法能有效利用关键字的各位信息，使哈希地址分布更均匀，减少冲突。

2.4 基数转换法

基数转换法：将关键字视为某一进制数，转换为另一进制后，选取部分位作为哈希地址。
- 例如，将关键字视为 $13$ 进制，转换为 $10$ 进制后作为哈希地址。

以 $343246$ 为例，计算如下：

$343246_{13} = 3 \times 13^5 + 4 \times 13^4 + 3 \times 13^3 + 2 \times 13^2 + 4 \times 13^1 + 6 \times 13^0 = 1235110_{10}$

3. 哈希冲突

哈希冲突（Hash Collision）：指不同的关键字经过同一个哈希函数后，得到相同的哈希地址，即 $key1 \ne key2$ ，但 $Hash(key1) == Hash(key2)$ ，这种现象称为哈希冲突。

理想情况下，哈希函数能够实现一一映射，每个关键字（ $key$ ）都对应唯一的存储位置（ $value$ ），无需处理冲突。但在实际应用中，即使哈希函数设计得再好，也难以完全避免不同关键字映射到同一地址的情况，即哈希冲突不可避免。

因此，必须采用一定的策略来解决哈希冲突。常见的哈希冲突解决方法主要有两大类：开放地址法（Open Addressing） 和 链地址法（Chaining）。

3.1 开放地址法

开放地址法（Open Addressing）：当哈希冲突发生时，通过探查哈希表中的其他「空地址」来存放冲突元素，直到找到空位为止。

具体做法是：当发生冲突时，按照如下公式计算下一个可用地址： $H(i) = (Hash(key) + F(i)) \mod m$ ，其中 $i = 1, 2, 3, ..., n$ ， $n \le m-1$ 。

$H(i)$ 表示第 $i$ 次探查得到的地址。每次冲突时，依次尝试新的地址，直到找到空位。
$Hash(key)$ 是哈希函数， $m$ 是哈希表长度，取模保证地址在表内。
$F(i)$ $F (i)$ 是探查增量，常见方式有：
- 线性探查： $F(i) = i$ ，即每次向后顺序查找。
- 二次探查： $F(i) = \pm i^2$ ，即以二次方步长向前后查找。
- 伪随机探查： $F(i)$ 为伪随机数序列。

举例说明：假设哈希表长度为 $11$ ，哈希函数 $Hash(key) = key \mod 11$ ，已存入 $28$ 、 $49$ 、 $18$ ，现插入 $38$ ，其哈希地址为 $5$ ，发生冲突。分别采用三种方法处理：

线性探查： $H(1) = (5 + 1) \mod 11 = 6$ （冲突）， $H(2) = (5 + 2) \mod 11 = 7$ （冲突）， $H(3) = (5 + 3) \mod 11 = 8$ （空位），将 $38$ 存入 $8$ 。
二次探查： $H(1) = (5 + 1^2) \mod 11 = 6$ （冲突）， $H(2) = (5 - 1^2) \mod 11 = 4$ （空位），将 $38$ 存入 $4$ 。
伪随机探查：假设伪随机数为 $9$ ， $H(1) = (5+9)\mod 11 = 3$ （空位），将 $38$ 存入 $3$ 。

如下图所示：

3.2 链地址法

链地址法（Chaining）：将哈希地址相同的元素以链表的形式存储在同一个槽位中。

链地址法是实际应用中更常用的哈希冲突解决方案。与开放地址法相比，链地址法实现更为简洁灵活。

假设哈希表长度为 $m$ ，哈希函数输出范围为 $[0, m - 1]$ ，则哈希表可以看作是 $m$ 个链表头指针组成的数组 $T$ 。

插入时，先通过 $Hash(key)$ 计算哈希地址 $i$ ，再将元素以链表节点的形式插入 $T[i]$ 指向的链表中。通常插入到表头，时间复杂度为 $O(1)$ 。
查询时，同样先计算哈希地址 $i$ ，然后遍历 $T[i]$ 链表，查找目标关键字。查找复杂度与链表长度 $k$ 成正比，即 $O(k)$ 。若哈希函数分布均匀， $k \approx n/m$ ， $n$ 为元素总数。

举例：将 $keys = [88, 60, 65, 69, 90, 39, 07, 06, 14, 44, 52, 70, 21, 45, 19, 32]$ 依次插入哈希表，哈希函数 $Hash(key) = key \mod 13$ ，表长 $m=13$ 。采用链地址法，插入结果如下图：

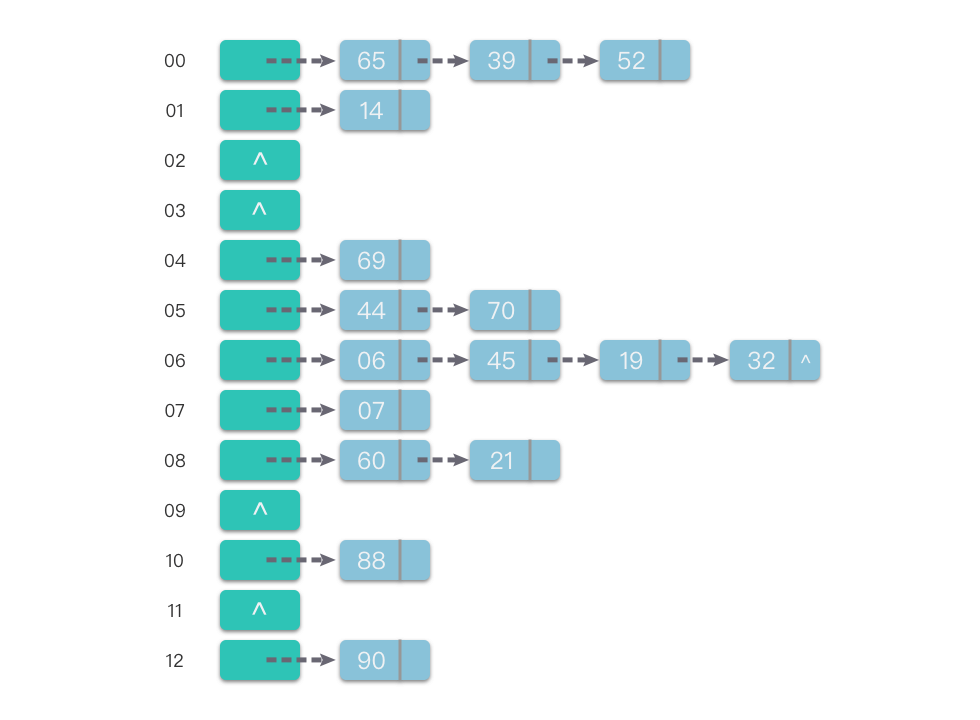
与开放地址法相比，链地址法虽然需要额外的链表节点存储空间，但能有效降低插入和查找时的平均查找长度。因为链地址法只需比较哈希地址相同的元素，而开放地址法可能需要探查多个不同地址的元素。

4. 哈希表总结

本文系统梳理了哈希表的基本原理与核心技术要点，内容涵盖哈希表的定义、哈希函数的设计、哈希冲突的本质及主流冲突解决策略。

哈希表（Hash Table）：一种通过哈希函数将关键字 $key$ 映射到存储位置，实现高效查找、插入和删除的数据结构。
哈希函数（Hash Function）：用于将关键字转换为哈希表索引的函数，其优劣直接影响哈希表的性能和冲突概率。
哈希冲突（Hash Collision）：指不同关键字经过哈希函数后映射到同一地址，是哈希表设计中不可避免的问题。

哈希表的设计与实现主要关注两个核心问题：

哈希函数的构建：常见方法包括直接定址法、除留余数法、平方取中法、基数转换法、数字分析法、折叠法、随机数法、乘积法、点积法等。合理选择和设计哈希函数有助于均匀分布关键字，降低冲突概率。
哈希冲突的解决：主流方法有两类，开放地址法和链地址法。
- 开放地址法：通过探查其他空槽位存放冲突元素，常见探查方式有线性探查、二次探查和伪随机探查等。
- 链地址法：将哈希地址相同的元素以链表形式存储在同一槽位，结构灵活，实际应用更为广泛。

合理的哈希函数设计与高效的冲突解决策略，是哈希表高性能的关键所在。

练习题目

参考资料

【博文】哈希算法及 python 字典的实现 – Tim's Path
【文章】哈希表 - LeetBook - 力扣（LeetCode）
【文章】漫画算法 - 小灰的算法之旅 - LeetBook - 力扣（LeetCode）
【博文】面试官：哈希表都不知道，你是怎么看懂 HashMap 的？ - 掘金
【博文】散列表 | Frank's Blog
【博文】哈希表 - OI Wiki
【博文】散列表（上）- 数据结构与算法之美 - 极客时间
【书籍】数据结构（C 语言版）- 严蔚敏著
【书籍】数据结构教程（第 3 版）- 唐发根著
【书籍】数据结构与算法 Python 语言描述 - 裘宗燕著