5.1 树与二叉树基础

ITCharge大约 12 分钟

5.1 树与二叉树基础

---

1. 树

1.1 树的定义

树（Tree）：由 $n \ge 0$ 个节点及其相互之间的关系组成的有限集合。当 $n = 0$ 时称为空树， $n > 0$ 时称为非空树。

之所以称为「树」，是因为这种数据结构的形态类似于一棵倒挂的树：根节点在上，叶子节点在下。如下图所示：

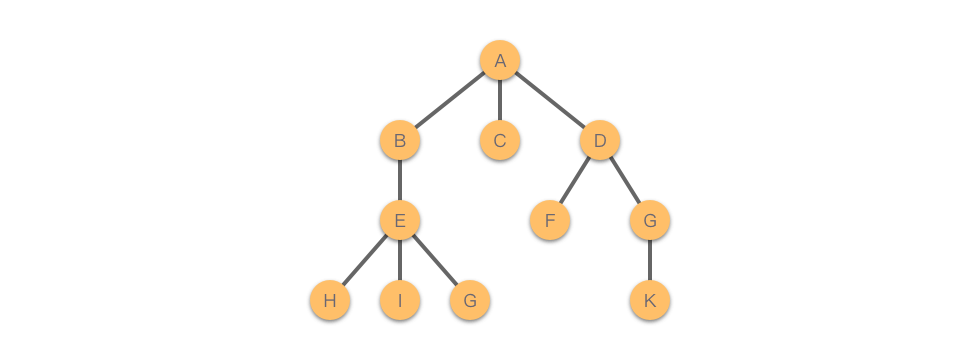
树结构具备以下基本特性：

仅有一个没有前驱的节点，称为 根节点（Root）。
除根节点外，其余每个节点都且仅有一个直接前驱节点。
每个节点（包括根节点）可以有零个或多个后继节点。
当 $n > 1$ 时，除根节点外的其余节点可分为 $m\ (m > 0)$ 个互不相交的有限集合 $T_1, T_2, ..., T_m$ ，每个集合本身又是一棵树，称为根的 子树（SubTree）。

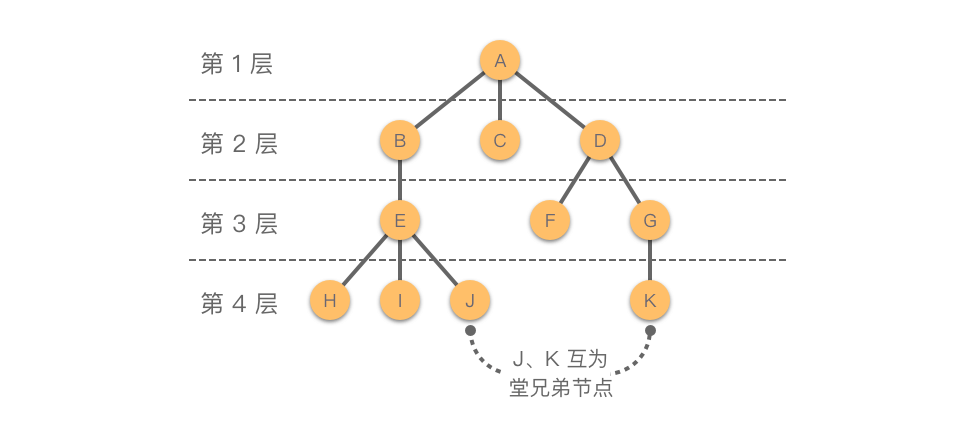
如下图所示，红色节点 $A$ 是根节点，除根节点外，存在 $3$ 棵互不相交的子树： $T_1(B, E, H, I, G)$ 、 $T_2(C)$ 、 $T_3(D, F, G, K)$ 。

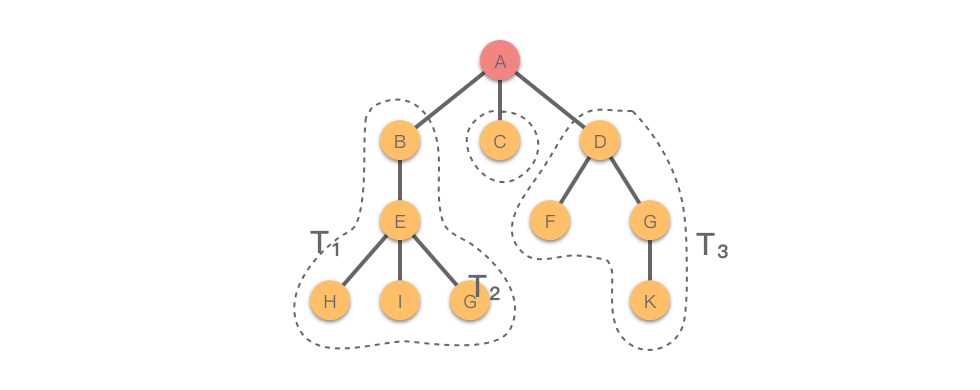
1.2 树的相关术语

下面介绍树结构中的常用基本术语。

1.2.1 节点分类

树的节点：由一个数据元素和若干指向其子树的分支组成。节点拥有的子树数量称为 节点的度。
叶子节点（终端节点）：度为 $0$ 的节点。例如图中 $C$ 、 $H$ 、 $I$ 、 $G$ 、 $F$ 、 $K$ 。
分支节点（非终端节点）：度大于 $0$ 的节点。例如图中 $A$ 、 $B$ 、 $D$ 、 $E$ 、 $G$ 。
树的度：树中所有节点的最大度数。例如图中树的度为 $3$ 。

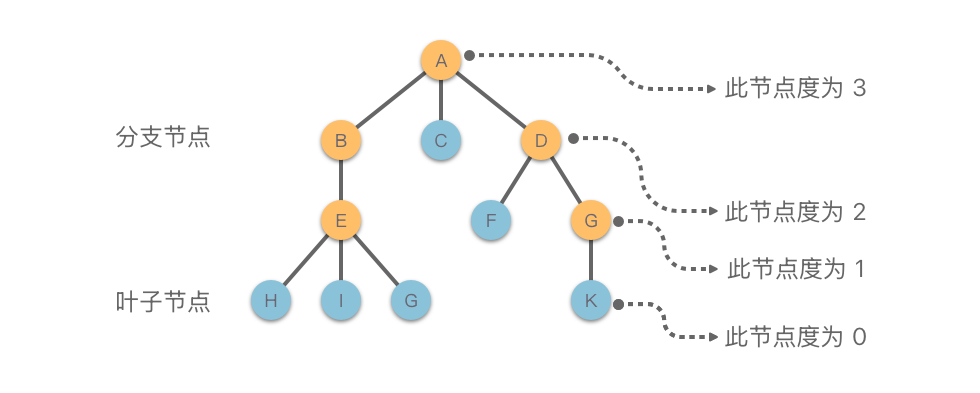
1.2.2 节点间关系

孩子节点（子节点）：某节点的子树的根节点。例如图中 $B$ 是 $A$ 的孩子节点。
父节点：拥有子节点的节点称为其子节点的父节点。例如图中 $B$ 是 $E$ 的父节点。
兄弟节点：同一父节点的不同子节点互为兄弟。例如图中 $F$ 、 $G$ 互为兄弟节点。

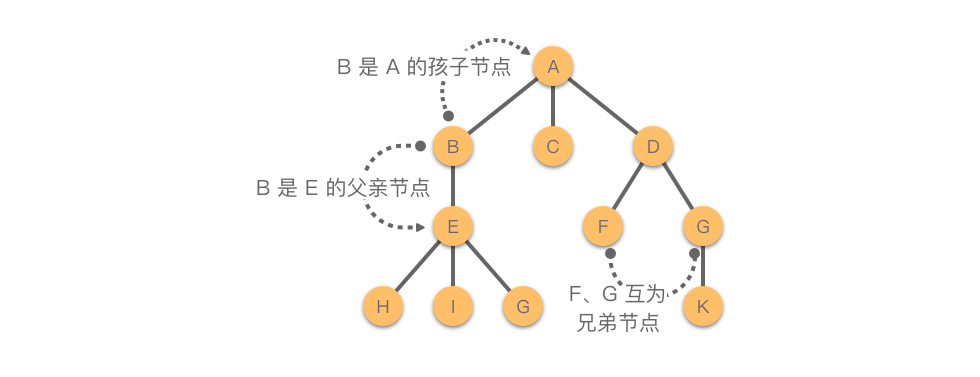
1.2.3 其他常用术语

节点的层次：从根节点开始，根为第 $1$ 层，根的子节点为第 $2$ 层，依此类推。
树的深度（高度）：树中节点的最大层数。例如图中树的深度为 $4$ 。
堂兄弟节点：父节点在同一层的节点互为堂兄弟。例如图中 $J$ 、 $K$ 互为堂兄弟节点。
路径：树中两个节点之间经过的节点序列。例如 $E$ 到 $G$ 的路径为 $E - B - A - D - G$ 。
路径长度：路径上经过的边数。例如 $E$ 到 $G$ 的路径长度为 $4$ 。
节点的祖先：从该节点到根节点路径上所有节点。例如 $H$ 的祖先为 $E$ 、 $B$ 、 $A$ 。
节点的子孙：以该节点为根的子树中所有节点。例如 $D$ 的子孙为 $F$ 、 $G$ 、 $K$ 。

1.3 树的分类

树按照节点子树之间是否可以交换位置，可以分为两大类：有序树 和 无序树。

有序树：每个节点的子树有严格的左右次序，子树之间的位置不可随意交换。例如二叉树就是典型的有序树。
无序树：每个节点的子树之间没有顺序要求，子树可以任意交换位置。

简而言之，有序树强调子树的排列顺序，结构唯一；无序树则只关注连接关系，不关心子树的排列顺序。

2. 二叉树

2.1 二叉树的定义

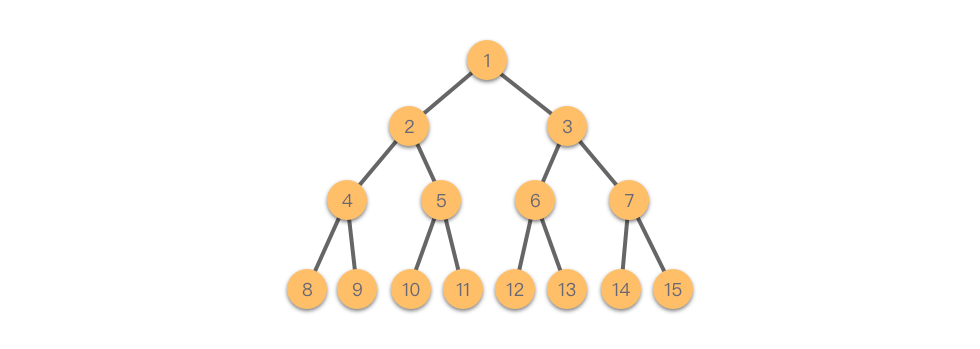
二叉树（Binary Tree）：是一种有序树，其中每个节点的度最多为 $2$ 。每个节点的两个分支分别称为 左子树 和 右子树，且左右子树的顺序不可交换。

如下图所示是一棵典型的二叉树：

二叉树还可以递归地定义为：

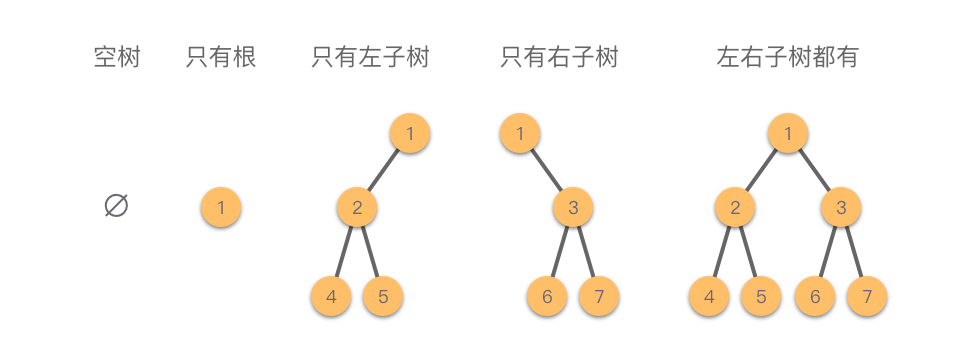
空树：即不包含任何节点的树。
非空树：由一个根节点和两棵互不相交的子树 $T_1$ 、 $T_2$ 组成， $T_1$ 称为左子树， $T_2$ 称为右子树，且 $T_1$ 、 $T_2$ 本身也都是二叉树。

简而言之，二叉树是一种每个节点最多有两个子树（左子树和右子树）的有序树，且左右子树的位置不可交换。换句话说，二叉树中每个节点的度都不超过 2。

二叉树在结构上可以分为以下 $5$ 种基本形态，如下图所示：

2.2 二叉树的基本性质

二叉树作为最常用的树形结构之一，具有以下基本性质：

第 $i$ 层的最大节点数：在二叉树中，第 $i$ 层最多有 $2^{i-1}$ 个节点（ $i \geq 1$ ）。
深度为 $k$ 的二叉树的最大节点数： $2^k - 1$ 。
任意一棵非空二叉树的第 $k$ 层至多有 $2^{k-1}$ 个节点。
节点数为 $n$ 的二叉树的最小深度： $\lceil \log_2(n+1) \rceil$ 。
叶子节点数与度为 $2$ 的节点数关系：二叉树中叶子节点数 $n_0$ 恰好比度为 $2$ 的节点数 $n_2$ 多 $1$ ，即 $n_0 = n_2 + 1$ 。
二叉树的边数： $n - 1$ ，其中 $n$ 为节点数。

这些性质对于分析二叉树的结构、空间复杂度和算法效率具有重要意义。

2.3 特殊的二叉树

下面介绍几类常见的特殊二叉树。

2.3.1 满二叉树

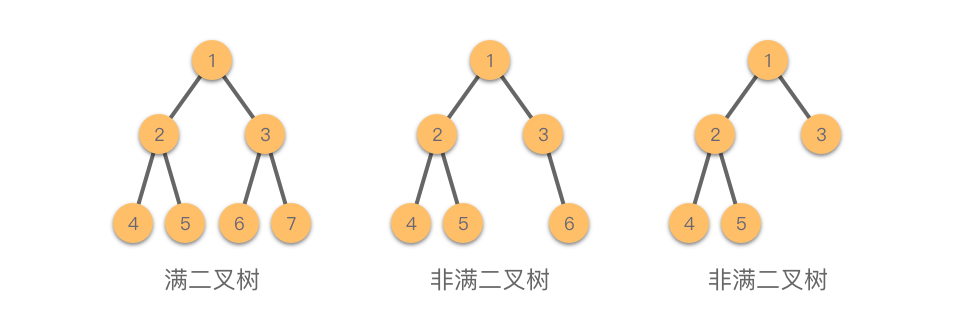
满二叉树（Full Binary Tree）：指所有非叶子节点均有左右两个子节点，且所有叶子节点都集中在同一层的二叉树。

满二叉树具有以下特征：

叶子节点全部位于最底层。
所有非叶子节点的度均为 $2$ 。
在相同深度的二叉树中，满二叉树的节点数和叶子节点数均为最大。

如果对满二叉树的节点自上而下、从左到右依次编号，根节点编号为 $1$ ，则深度为 $k$ 的满二叉树最后一个节点的编号为 $2^k - 1$ 。

如下图所示，展示了满二叉树与非满二叉树的示例：

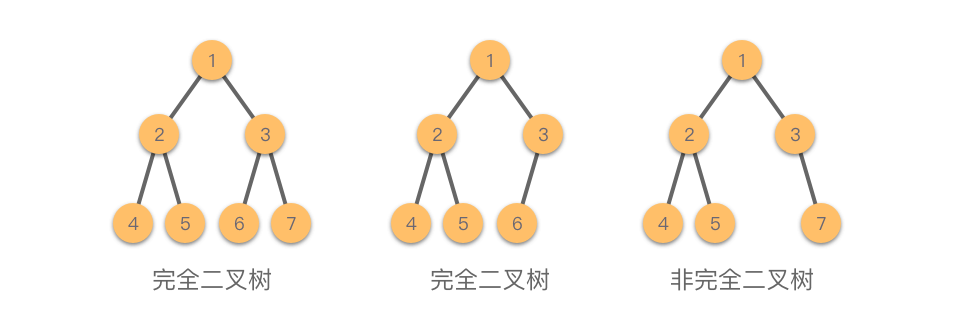
2.3.2 完全二叉树

完全二叉树（Complete Binary Tree）：一种特殊的二叉树，要求除了最后一层外，每一层的节点数都达到最大，且最后一层的所有节点都连续排列在最左侧。

完全二叉树的主要特征如下：

叶子节点只可能出现在最后两层。
最底层的叶子节点必须依次排列在最左侧。
倒数第二层如果有叶子节点，则这些节点必须集中在右侧。
如果某节点的度为 $1$ ，则该节点只能有左孩子，不存在只有右孩子的情况。
在节点数相同的二叉树中，完全二叉树的深度最小。

完全二叉树也可以通过节点编号来定义：从根节点开始，按层次自上而下、从左到右依次编号（根为 $1$ ）。若一棵深度为 $k$ 、节点数为 $n$ 的二叉树，其每个节点与深度为 $k$ 的满二叉树中编号 $1$ 到 $n$ 的节点一一对应，则该树为完全二叉树。

下面通过示例图进行说明：

2.3.3 二叉搜索树

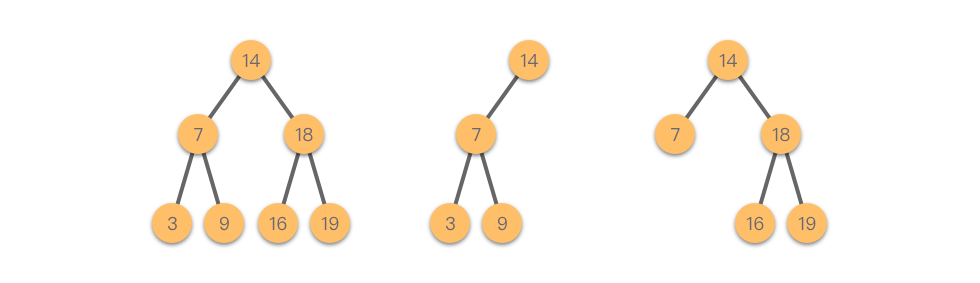
二叉搜索树（Binary Search Tree, BST），又称二叉查找树、有序二叉树或排序二叉树，是一种特殊的二叉树结构。其定义如下：
对于任意一个节点，如果其左子树非空，则左子树所有节点的值均小于该节点的值；
对于任意一个节点，如果其右子树非空，则右子树所有节点的值均大于该节点的值；
左右子树本身也都是二叉搜索树；
空树也被视为二叉搜索树。

二叉搜索树的结构保证了对任意节点的中序遍历结果是递增有序的。下图展示了三棵典型的二叉搜索树：

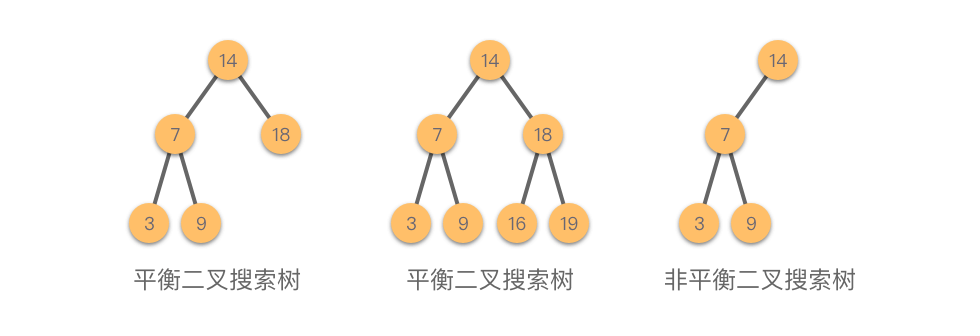
2.3.4 平衡二叉搜索树

平衡二叉搜索树（Balanced Binary Search Tree, BBST）：是一类结构上保持平衡的二叉搜索树。其核心特性是任意节点的左右子树高度差的绝对值不超过 $1$ ，且左右子树本身也都是平衡二叉搜索树。通过这种结构，平衡二叉搜索树能够保证插入、查找和删除操作的时间复杂度均为 $O(\log n)$ 。最早提出的平衡二叉搜索树是 AVL 树（Adelson-Velsky and Landis Tree）。

AVL 树的主要性质如下：

空树是一棵 AVL 树。
如果二叉树 $T$ 是 AVL 树，则 $T$ 的左右子树也都是 AVL 树，且满足 $|h(\text{left}) - h(\text{right})| \le 1$ ，其中 $h(\text{left})$ 和 $h(\text{right})$ 分别为左、右子树的高度。
AVL 树的高度始终保持在 $O(\log n)$ 。

下图中，前两棵树为平衡二叉搜索树，最后一棵树不是平衡二叉搜索树，因为其某节点的左右子树高度差超过 $1$ 。

2.4 二叉树的存储结构

二叉树常见的存储方式有两种：「顺序存储结构」和「链式存储结构」。下面分别介绍这两种方式。

2.4.1 二叉树的顺序存储结构

顺序存储结构通常使用一维数组来保存二叉树的所有节点。节点在数组中的位置按照完全二叉树的层序编号排列：自上而下、从左到右依次存放。如果某个节点不存在，则在数组对应位置填充「空节点」。

例如，堆排序和优先队列中的二叉堆结构就是采用顺序存储结构实现的。

以节点值为 $[1, 2, 3, 4, 5, 6, 7]$ 的完全二叉树为例，其顺序存储结构如下图所示。

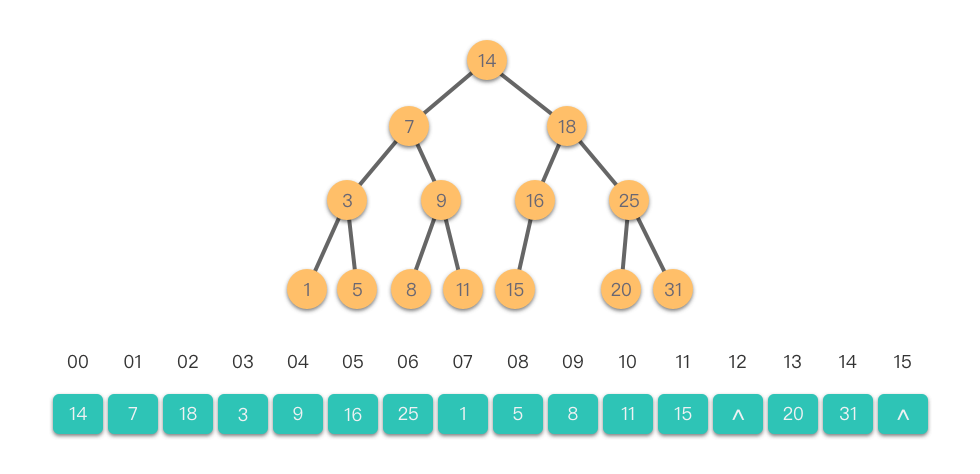
通过顺序存储结构，节点之间的关系可以通过下标直接计算得到：

如果某节点（非叶子节点）下标为 $i$ ，则其左孩子下标为 $2 \times i + 1$ ，右孩子下标为 $2 \times i + 2$ 。
如果某节点（非根节点）下标为 $i$ ，则其父节点下标为 $(i - 1) // 2$ （ $//$ 表示整除）。

顺序存储结构非常适合 完全二叉树（尤其是满二叉树），因为可以充分利用数组空间，节点排列紧凑。但对于一般二叉树，若存在大量空节点，则会造成空间浪费。此外，顺序存储结构不利于二叉树的插入和删除操作，灵活性较差。当二叉树结构和规模经常变化时，更推荐使用链式存储结构。

2.4.2 二叉树的链式存储结构

在链式存储结构中，二叉树的每个节点通常包含三个部分：一个数据域 $val$ 用于存放节点的值，两个指针域 $left$ 和 $right$ 分别指向左、右子节点。当某个子节点不存在时，相应的指针为 None（或 null）。这种结构如下图所示：

其对应的代码实现如下：

class TreeNode:
    """
    二叉树节点定义（链式存储结构）

    属性:
        val: 节点存储的值
        left: 指向左子节点的指针（无左子节点时为 None）
        right: 指向右子节点的指针（无右子节点时为 None）
    """
    def __init__(self, val=0, left=None, right=None):
        self.val = val          # 节点的值
        self.left = left        # 左子节点指针
        self.right = right      # 右子节点指针

以节点值为 $[1, 2, 3, 4, 5, 6, 7]$ 的完全二叉树为例，其链式存储结构如下图所示。

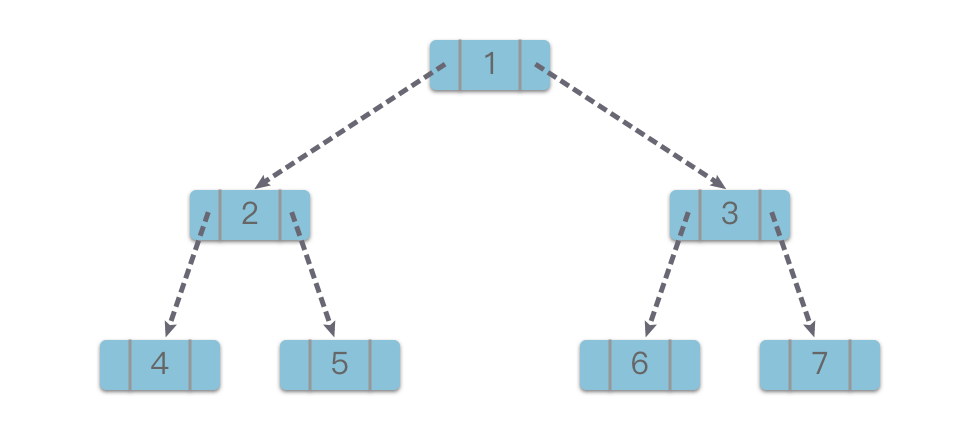
链式存储结构具有高度的灵活性和便利性。其节点数量仅受限于系统可用内存，且通常比顺序存储结构更节省空间（指针域的空间开销与节点数成线性关系）。此外，链式结构便于进行插入、删除等操作，因此在实际应用中，二叉树大多采用链式存储结构。

3. 总结

树是一种层次化的非线性数据结构，由节点和边组成，具有一个根节点和若干子树。二叉树是树的一种特殊形式，每个节点最多有两个子节点（左子树和右子树）。

二叉树的核心特性：

层次性：二叉树以根节点为起点，节点自上而下、由左至右分层排列，形成清晰的层级结构。
递归性：每个节点的左右子树本身也是二叉树，天然适合递归定义与处理。
有序性：每个节点的左、右子树位置固定，不能随意交换，保证结构的唯一性和有序性。

二叉树常见类型：

满二叉树：除叶子节点外，每个节点都有两个子节点
完全二叉树：除最后一层外，其他层都被填满，最后一层从左到右填充
二叉搜索树：左子树所有节点值小于根节点，右子树所有节点值大于根节点
平衡二叉树：左右子树高度差不超过1，保证操作效率

二叉树存储方式：

顺序存储：用数组存储，适合完全二叉树，空间利用率高
链式存储：用指针连接，灵活性好，便于动态操作

参考链接

【书籍】数据结构教程第 3 版 - 唐发根著
【书籍】大话数据结构程杰著
【书籍】算法训练营陈小玉著
【博文】二叉树理论基础 - 代码随想录
【博文】二叉树基础 - 袁厨的算法小屋