5.2 二叉树的遍历

ITCharge大约 15 分钟

5.2 二叉树的遍历

---

1. 二叉树的遍历简介

二叉树的遍历：是指从根节点出发，按照特定顺序依次访问二叉树中的所有节点，确保每个节点被且仅被访问一次。

在实际应用中，常常需要按照一定的顺序访问二叉树的每个节点，以便查找特定节点或处理全部节点。例如，可以依次输出节点的值、统计满足某条件的节点数量等。这里的「访问」通常指对节点执行某种操作。

根据二叉树的递归结构是由根节点、左子树和右子树组成的，只要依次遍历这三部分，就能遍历整棵二叉树。

按照遍历顺序的不同，二叉树的遍历方式主要分为两大类：

深度优先遍历（DFS）：根据节点访问顺序的不同，理论上有 $6$ 种遍历方式。若约定先遍历左子树再遍历右子树，常用的有 $3$ 种：前序遍历、中序遍历、后序遍历。
广度优先遍历（BFS）：按照层次自上而下、每层从左到右依次访问所有节点，称为 层序遍历。

这些遍历方式为二叉树的各种操作和算法奠定了基础。

2. 二叉树前序遍历

二叉树前序遍历（Preorder Traversal）：是指按照「根节点 → 左子树 → 右子树」的顺序依次访问二叉树的所有节点。

具体规则如下：

如果二叉树为空，直接返回；
如果二叉树非空，则：

访问根节点；
递归前序遍历左子树；
递归前序遍历右子树。

前序遍历本质上是一个递归过程。无论遍历哪一棵子树，始终遵循「先访问根节点，再遍历左子树，最后遍历右子树」的顺序。

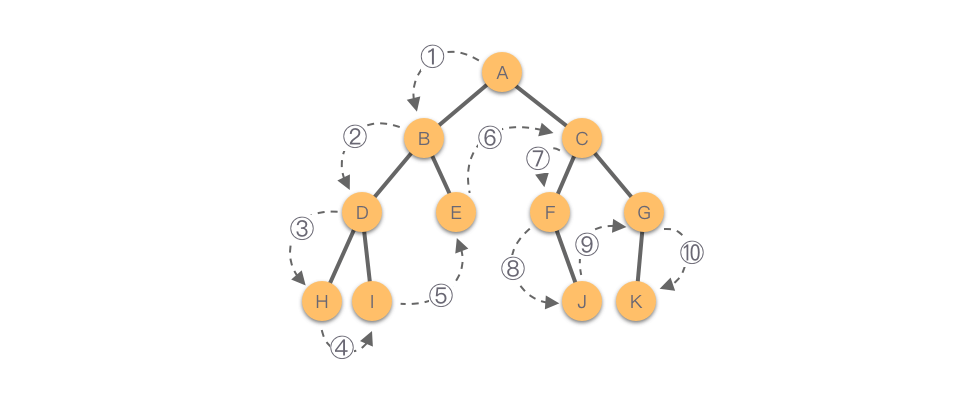
如下图所示，该二叉树的前序遍历结果为： $A - B - D - H - I - E - C - F - J - G - K$ 。

2.1 二叉树前序遍历的递归实现

二叉树前序遍历递归实现的基本步骤：

如果当前节点为空，直接返回；
访问当前节点（根节点）；
递归遍历左子树；
递归遍历右子树。

前序遍历的递归实现代码如下：

class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        """
        二叉树的前序遍历（递归实现）
        参数:
            root: TreeNode，二叉树的根节点
        返回:
            List[int]，前序遍历的节点值列表
        """
        res = []  # 用于存储遍历结果

        def preorder(node):
            if not node:
                return  # 递归终止条件：节点为空
            res.append(node.val)      # 1. 访问根节点
            preorder(node.left)       # 2. 递归遍历左子树
            preorder(node.right)      # 3. 递归遍历右子树

        preorder(root)  # 从根节点开始递归
        return res

2.2 二叉树前序遍历的非递归实现

递归实现前序遍历时，实际上是借助系统调用栈来完成的。我们同样可以用一个显式栈 $stack$ 来手动模拟递归过程，实现前序遍历。

前序遍历的访问顺序为：根节点 → 左子树 → 右子树。由于栈具有「后进先出」的特性，为了保证遍历顺序正确，入栈时应先将右子节点压入，再将左子节点压入，这样弹出时会先访问左子树，再访问右子树。

具体实现步骤如下：

如果二叉树为空，直接返回。
初始化一个栈，将根节点压入栈中。
当栈不为空时，重复以下操作：
1. 弹出栈顶节点 $node$ ，访问该节点。
2. 如果 $node$ 的右子节点存在，则将其压入栈中。
3. 如果 $node$ 的左子节点存在，则将其压入栈中。

这样即可实现前序遍历的非递归（显式栈）写法。

class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """
        二叉树的前序遍历（非递归/显式栈实现）
        参数:
            root: Optional[TreeNode]，二叉树的根节点
        返回:
            List[int]，前序遍历的节点值列表
        """
        if not root:  # 特判：二叉树为空，直接返回空列表
            return []

        res = []              # 用于存储遍历结果
        stack = [root]        # 初始化栈，根节点先入栈

        while stack:          # 当栈不为空时循环
            node = stack.pop()        # 弹出栈顶节点
            res.append(node.val)      # 访问当前节点（根节点）
            # 注意：先右后左，保证左子树先被遍历
            if node.right:            # 如果右子节点存在，先将其入栈
                stack.append(node.right)
            if node.left:             # 如果左子节点存在，再将其入栈
                stack.append(node.left)

        return res  # 返回前序遍历结果

3. 二叉树中序遍历

二叉树中序遍历（Inorder Traversal） 的基本规则如下：
如果二叉树为空，直接返回。
如果二叉树非空，则依次执行：
递归遍历左子树（中序方式）；
访问当前根节点；
递归遍历右子树（中序方式）。

中序遍历本质上是一个递归过程。无论遍历哪一棵子树，始终遵循「先左子树，后根节点，最后右子树」的顺序。每到一个节点，先深入其左子树，左子树遍历完毕后访问该节点本身，最后再遍历其右子树。

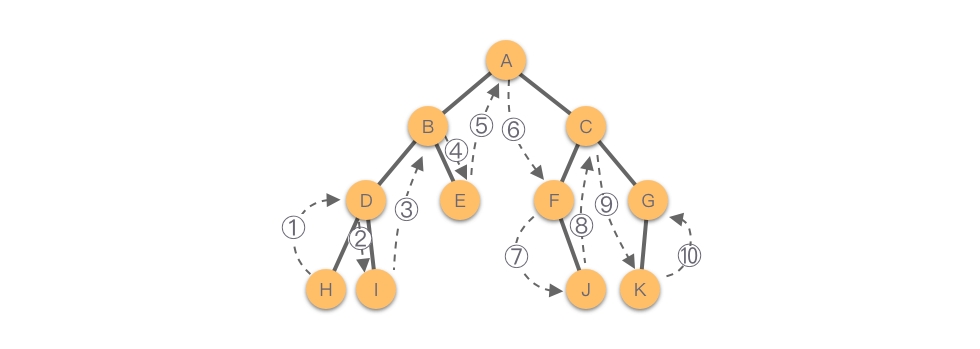
如下图所示，该二叉树的中序遍历结果为： $H - D - I - B - E - A - F - J - C - K - G$ 。

3.1 二叉树中序遍历的递归实现

二叉树的序遍历递归实现的基本步骤：

如果当前节点为空，直接返回。
递归遍历左子树。
访问当前节点。
递归遍历右子树。

对应的递归实现代码如下：

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        """
        二叉树中序遍历（递归实现）

        参数:
            root: TreeNode，二叉树的根节点
        返回:
            List[int]，中序遍历的节点值列表
        """
        res = []  # 用于存储遍历结果

        def inorder(node):
            if not node:
                return  # 递归终止条件：节点为空
            inorder(node.left)         # 递归遍历左子树
            res.append(node.val)       # 访问当前节点
            inorder(node.right)        # 递归遍历右子树

        inorder(root)  # 从根节点开始递归
        return res     # 返回中序遍历结果

3.2 二叉树中序遍历的非递归实现

我们可以通过显式维护一个栈 $stack$ ，来模拟递归实现的中序遍历过程。

与前序遍历不同，中序遍历要求在访问根节点前，必须先遍历完其左子树。因此，只有在左子树全部入栈后，当前节点才能出栈并被访问。

具体做法是：从根节点出发，不断将当前节点压入栈中，并向左移动，直到没有左子节点为止。此时弹出栈顶节点，访问该节点，然后转向其右子树，重复上述过程。这样可以确保遍历顺序严格按照「左-根-右」进行。

中序遍历的非递归（显式栈）实现步骤如下：

如果二叉树为空，直接返回。
初始化一个空栈。
当当前节点不为空或栈不为空时，重复以下操作：
1. 如果当前节点不为空，不断将其压入栈，并向左移动，直到左子节点为空。
2. 如果当前节点为空，说明已到达最左侧，弹出栈顶节点 $node$ ，访问该节点，然后将当前节点指向 $node$ 的右子节点，继续上述循环。

二叉树中序遍历的非递归实现代码如下：

class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """
        二叉树中序遍历（非递归/显式栈实现）

        参数:
            root: Optional[TreeNode]，二叉树的根节点
        返回:
            List[int]，中序遍历的节点值列表
        """
        res = []    # 用于存储遍历结果
        stack = []  # 显式栈，用于模拟递归过程
        cur = root  # 当前遍历的节点指针

        while cur or stack:  # 只要当前节点不为空或栈不为空就继续
            # 不断向左子树深入，将沿途节点全部入栈
            while cur:
                stack.append(cur)      # 当前节点入栈
                cur = cur.left         # 继续遍历左子树

            # 此时已到达最左侧，弹出栈顶节点
            node = stack.pop()         # 弹出最左侧节点
            res.append(node.val)       # 访问该节点（中序遍历的“根”）
            cur = node.right           # 转向右子树，继续上述过程

        return res

4. 二叉树后序遍历

二叉树后序遍历（Postorder Traversal） 的基本规则如下：
如果二叉树为空，直接返回。
如果二叉树非空，则依次执行：
递归遍历左子树（后序方式）。
递归遍历右子树（后序方式）。
访问根节点。

后序遍历的本质是递归地先处理左子树，再处理右子树，最后处理根节点。无论遍历到哪一棵子树，始终遵循「左-右-根」的顺序。

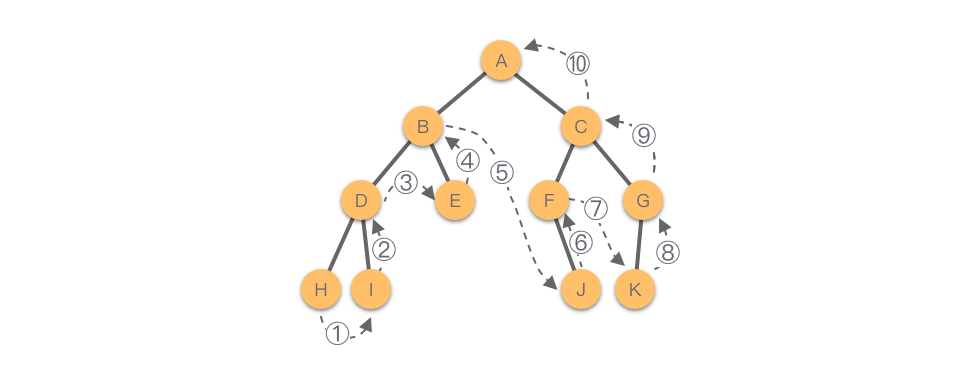
如下图所示，该二叉树的后序遍历结果为： $H - I - D - E - B - J - F - K - G - C - A$ 。

4.1 二叉树后序遍历的递归实现

后序遍历递归实现的核心思想是：对于每个节点，先处理其左子树，再处理右子树，最后访问节点本身。具体步骤如下：

如果当前节点为空，直接返回。
递归遍历左子树。
递归遍历右子树。
访问当前节点（即处理节点值）。

下面是二叉树后序遍历的递归实现代码：

class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        """
        二叉树后序遍历（递归实现）
        参数:
            root: TreeNode，二叉树的根节点
        返回:
            List[int]，后序遍历的节点值列表
        """
        res = []  # 用于存储遍历结果

        def postorder(node):
            if not node:
                return
            # 递归遍历左子树
            postorder(node.left)
            # 递归遍历右子树
            postorder(node.right)
            # 访问当前节点
            res.append(node.val)

        postorder(root)
        return res

4.2 二叉树后序遍历的非递归实现

后序遍历可以通过显式栈 $stack$ 来模拟递归过程。与前序和中序遍历不同，后序遍历要求在左右子树都访问完成后，才能访问根节点。因此，必须确保：当前节点在其左右孩子节点都访问完毕之前不能出栈。

后序遍历的非递归实现可以通过如下方式优化理解：

从根节点出发，将其依次压入栈中，并不断向左深入，直到到达最左侧节点。
每次弹出栈顶节点，判断其右子树是否已被访问：
- 如果已访问，则访问该节点；
- 如果未访问，则将该节点重新压入栈，并转而遍历其右子树。

具体步骤如下：

如果二叉树为空，直接返回。
初始化一个空栈 $stack$ ，并用 $prev$ 记录上一个访问的节点。
当当前节点不为空或栈不为空时，循环执行：
1. 不断将当前节点压入栈，并向左移动，直到最左侧节点。
2. 弹出栈顶节点 $node$ 。
3. 若 $node$ 没有右子树，或右子树已被访问，则访问 $node$ ，更新 $prev$ ，并将当前节点设为空。
4. 否则，将 $node$ 重新压回栈，转而遍历其右子树。

这样即可实现二叉树的后序遍历非递归写法。

class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        """
        二叉树后序遍历（非递归/显式栈实现）
        参数:
            root: Optional[TreeNode]，二叉树的根节点
        返回:
            List[int]，后序遍历的节点值列表
        """
        res = []        # 用于存储遍历结果
        stack = []      # 显式栈，用于模拟递归过程
        prev = None     # 记录上一个访问的节点，用于判断右子树是否已访问

        while root or stack:  # 只要当前节点不为空或栈不为空就继续遍历
            # 一直向左走，将所有左子节点入栈
            while root:
                stack.append(root)      # 当前节点入栈
                root = root.left        # 继续遍历左子树

            node = stack.pop()          # 弹出栈顶节点，准备访问或遍历其右子树

            # 判断是否可以访问当前节点
            # 1. 没有右子树
            # 2. 右子树已经访问过（即上一次访问的节点是当前节点的右子节点）
            if not node.right or node.right == prev:
                res.append(node.val)    # 访问当前节点
                prev = node             # 更新上一次访问的节点
                root = None             # 当前节点已访问，重置root，防止重复入栈
            else:
                # 右子树还未访问，当前节点重新入栈，转而遍历右子树
                stack.append(node)
                root = node.right

        return res

5. 二叉树层序遍历

二叉树层序遍历（Level Order Traversal）的基本规则为：指按照从上到下、从左到右的顺序，逐层依次访问二叉树的所有节点。
如果二叉树为空，直接返回。
如果二叉树非空，则：
先访问第 $1$ 层（根节点）；
再访问第 $2$ 层的所有节点；
依次类推，直到访问到最底层的所有节点。

层序遍历本质上是一种广度优先搜索（BFS）过程。遍历时，先访问每一层的所有节点，再进入下一层，并且同一层的节点总是从左到右依次访问。

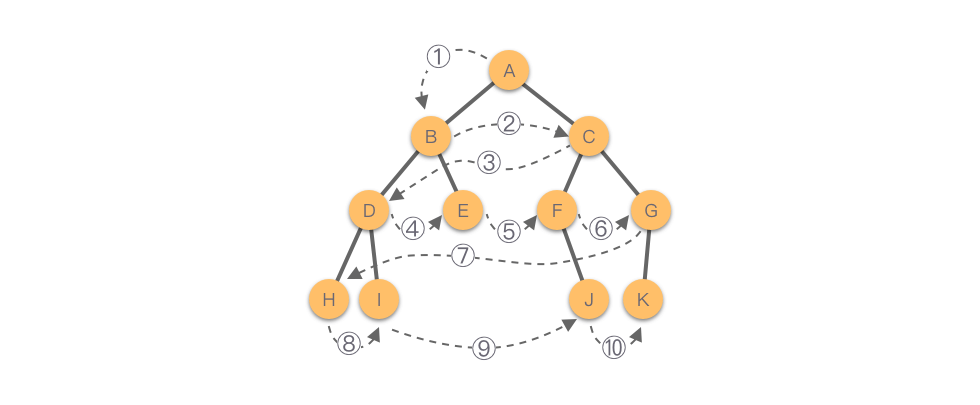
如下图所示，该二叉树的层序遍历结果为： $A - B - C - D - E - F - G - H - I - J - K$ 。

层序遍历通常借助队列（Queue）来实现。具体流程如下：

如果二叉树为空，直接返回。
将根节点加入队列。
当队列不为空时，重复以下操作：
1. 记录当前队列长度 $s_i$ （即当前层的节点数）。
2. 依次从队列中取出这 $s_i$ 个节点，访问它们，并将它们的左右子节点（如存在）加入队列。
队列为空时，遍历结束。

二叉树层序遍历的代码实现如下：

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        """
        二叉树层序遍历（广度优先搜索，BFS）
        返回每一层的节点值组成的二维列表
        """
        if not root:
            return []  # 空树直接返回空列表

        from collections import deque  # 推荐使用 deque 提高队列效率
        queue = deque([root])  # 初始化队列，根节点入队
        order = []             # 用于存储最终结果

        while queue:
            level = []                 # 存储当前层的节点值
            size = len(queue)          # 当前层的节点数量
            for _ in range(size):
                curr = queue.popleft() # 弹出队首节点
                level.append(curr.val) # 访问当前节点
                if curr.left:
                    queue.append(curr.left)   # 左子节点入队
                if curr.right:
                    queue.append(curr.right)  # 右子节点入队
            if level:
                order.append(level)     # 当前层结果加入总结果

        return order

6. 总结

6.1 算法特点对比

遍历方式	访问顺序	递归实现	非递归实现	空间复杂度	时间复杂度
前序遍历	根 → 左 → 右	简单直观	使用栈，先右后左入栈	O(h)	O(n)
中序遍历	左 → 根 → 右	简单直观	使用栈，先左后右	O(h)	O(n)
后序遍历	左 → 右 → 根	简单直观	使用栈，需要标记访问状态	O(h)	O(n)
层序遍历	按层从左到右	不适用	使用队列，BFS思想	O(w)	O(n)

注：h 为树的高度，w 为树的最大宽度，n 为节点总数

6.2 优缺点分析

前序遍历

优点：
- 递归实现简单直观，易于理解
- 适合需要先处理根节点再处理子节点的场景
- 常用于树的复制、序列化等操作
缺点：
- 非递归实现需要特别注意入栈顺序
- 对于深度很大的树，递归可能导致栈溢出

中序遍历

优点：
- 对于二叉搜索树，中序遍历得到有序序列
- 递归实现逻辑清晰
- 适合需要按顺序处理节点的场景
缺点：
- 非递归实现相对复杂
- 需要理解"左-根-右"的访问时机

后序遍历

优点：
- 适合需要先处理子节点再处理父节点的场景
- 常用于树的删除、后序表达式计算等
- 递归实现简单
缺点：
- 非递归实现最复杂，需要额外的访问状态标记
- 理解难度较高

层序遍历

优点：
- 直观反映树的层次结构
- 适合需要按层处理节点的场景
- 非递归实现相对简单
缺点：
- 不适用于递归实现
- 空间复杂度可能较高（对于宽树）

练习题目

参考资料

【书籍】数据结构教程第 3 版 - 唐发根著
【书籍】大话数据结构程杰著
【书籍】算法训练营陈小玉著
【题解】LeetCode 二叉树前序遍历（递归法 + 非递归法）- 二叉树的前序遍历 - 力扣
【题解】二叉树遍历通解（递归和迭代解法）- 完全模拟递归 - 二叉树的后序遍历 - 力扣
【题解】迭代后序遍历 - 二叉树的后序遍历 - 力扣