5.5 线段树（一）

---

1. 线段树简介

1.1 线段树的定义

线段树（Segment Tree）：一种用于高效处理区间查询和区间修改的二叉树结构。它将一个区间不断二分，每个节点管理一个区间，叶子节点对应单个元素，内部节点则代表其子区间的合并结果。这样可以在 $O(\log n)$ 时间内完成区间相关操作。

线段树就像「区间的管家」：每个节点专管一个区间 $[left, right]$，叶子节点只负责一个元素（$left = right$），非叶子节点则把区间一分为二，左孩子管 $[left, mid]$，右孩子管 $[mid+1, right]$，其中 $mid = (left + right) // 2$。整棵树自顶向下分工明确，根节点总揽全局。无论是单点修改、区间修改还是区间查询，都能在 $O(\log n)$ 时间内完成，非常适合处理大规模区间数据。

下图展示了区间 $[0, 7]$ 的线段树结构：

区间 [0, 7] 对应的线段树

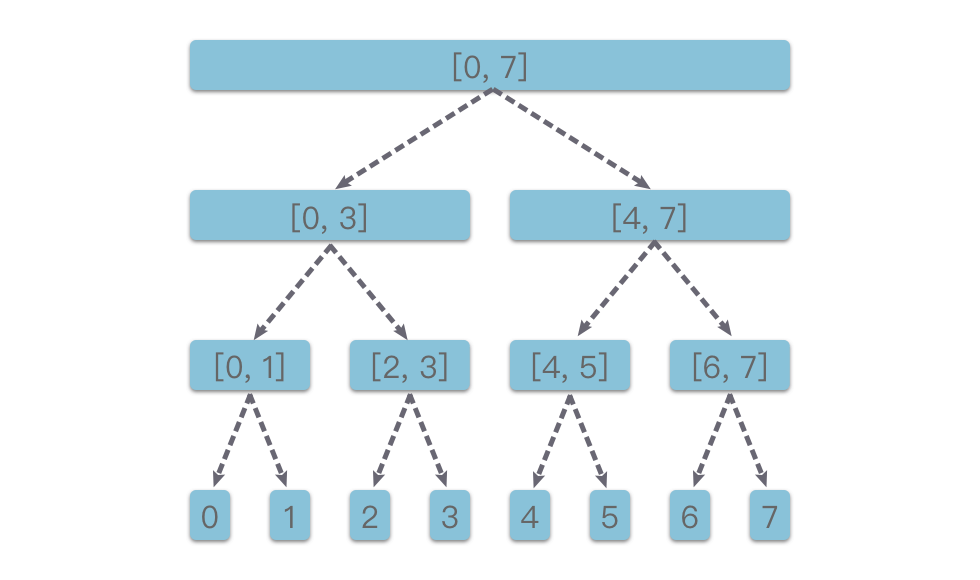
1.2 线段树的特点

线段树的核心特点如下：

1. 每个节点对应一个区间。
2. 根节点管理整个区间（如 $[1, n]$）。
3. 叶子节点对应单个元素区间（$[x, x]$）。
4. 每个内部节点 $[left, right]$ 的左子节点为 $[left, mid]$，右子节点为 $[mid + 1, right]$，其中 $mid = (left + right) // 2$（向下取整）。

2. 线段树的构建

2.1 线段树的存储结构

在二叉树中，我们常见的存储方式有「链式存储」和「顺序存储」。线段树同样可以采用这两种方式实现，但由于其结构接近完全二叉树，使用「顺序存储结构」（即数组）更加高效和简洁。

线段树的数组存储编号规则如下：

• 根节点编号为 $0$。
• 如果某节点编号为 $i$，则其左孩子编号为 $2 \times i + 1$，右孩子编号为 $2 \times i + 2$。
• 如果某节点编号为 $i$（且 $i > 0$），其父节点编号为 $(i - 1) // 2$。

这样，我们可以用一个数组来存储整棵线段树。那么数组的大小如何确定呢？

• 理想情况下，$n$ 个叶子节点构成的线段树是一棵满二叉树，总节点数为 $2 \times n - 1$。因此，数组大小取 $2 \times n$ 足够。
• 但实际上，为了适配任意长度的区间，线段树的深度为 $\lceil \log_2 n \rceil$，最坏情况下节点总数约为 $2^{\lceil \log_2 n \rceil + 1} - 1$，可近似为 $4 \times n$。因此，通常分配 $4 \times n$ 大小的数组即可保证安全。

2.2 线段树的构建方法

线段树父子节点下标关系

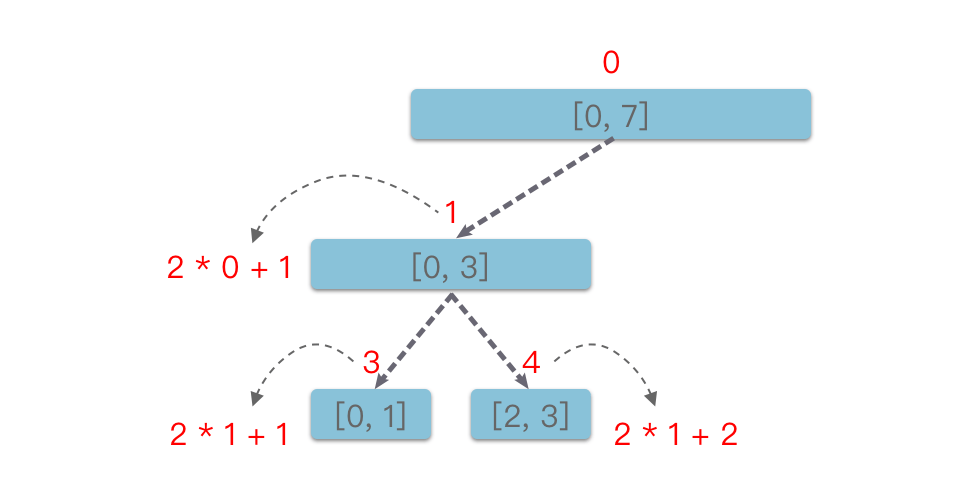
如上图所示，编号为 $i$ 的节点，其左右孩子编号分别为 $2 \times i + 1$ 和 $2 \times i + 2$。因此，线段树的构建非常适合递归实现。具体步骤如下：

1. 如果当前区间为叶子节点（$left == right$），则节点值为对应元素值。
2. 如果为非叶子节点，递归构建左、右子树。
3. 当前节点的区间值（如区间和、最大值、最小值等）由左右子节点的值合并得到。

线段树的构建实现代码如下：

# 线段树的节点类
class TreeNode:
    def __init__(self, val=0):
        self.left = -1          # 区间左边界
        self.right = -1         # 区间右边界
        self.val = val          # 节点值（区间值，如区间和、区间最大值等）
        self.lazy_tag = None    # 区间延迟更新标记（如区间加法、区间赋值等懒惰标记）

# 线段树类
class SegmentTree:
    def __init__(self, nums, function):
        """
        :param nums: 原始数据数组
        :param function: 区间聚合函数（如 sum, max, min 等）
        """
        self.size = len(nums)
        # 线段树最多需要 4 * n 个节点，使用数组存储
        self.tree = [TreeNode() for _ in range(4 * self.size)]
        self.nums = nums
        self.function = function
        if self.size > 0:
            self.__build(0, 0, self.size - 1)

    def __build(self, index, left, right):
        """
        递归构建线段树
        :param index: 当前节点在数组中的下标
        :param left: 当前节点管理的区间左端点
        :param right: 当前节点管理的区间右端点
        """
        self.tree[index].left = left
        self.tree[index].right = right
        if left == right:
            # 叶子节点，直接赋值为原数组对应元素
            self.tree[index].val = self.nums[left]
            return

        mid = left + (right - left) // 2
        left_index = index * 2 + 1      # 左子节点下标
        right_index = index * 2 + 2     # 右子节点下标
        self.__build(left_index, left, mid)         # 构建左子树
        self.__build(right_index, mid + 1, right)   # 构建右子树
        self.__pushup(index)                        # 更新当前节点的区间值

    def __pushup(self, index):
        """
        向上更新当前节点的区间值
        :param index: 当前节点在数组中的下标
        """
        left_index = index * 2 + 1      # 左子节点下标
        right_index = index * 2 + 2     # 右子节点下标
        # 当前节点的区间值由左右子节点的区间值聚合得到
        self.tree[index].val = self.function(
            self.tree[left_index].val,
            self.tree[right_index].val
        )

这里的 function 参数用于指定线段树在区间合并时所采用的聚合函数。根据具体题目需求，可以灵活传入如求和（sum）、取最大值（max）、取最小值（min）等常见操作，实现不同类型的区间查询。

3. 线段树的基本操作

线段树的基本操作包括：单点更新、区间查询和区间更新。下面依次介绍。

3.1 单点更新

单点更新：将 $nums[i]$ 修改为 $val$。

递归实现思路如下：

1. 如果当前节点为叶子节点（$left == right$），直接更新其值。
2. 否则，判断 $i$ 属于左子树还是右子树，递归更新对应子树。
3. 更新完后，向上合并，重新计算当前节点的区间值。

单点更新的代码如下：

def update_point(self, i, val):
    """
    单点更新：将原数组 nums[i] 的值修改为 val，并同步更新线段树
    :param i: 需要更新的元素下标
    :param val: 新的值
    """
    self.nums[i] = val  # 更新原数组
    self.__update_point(i, val, 0, 0, self.size - 1)  # 从根节点递归更新线段树

def __update_point(self, i, val, index, left, right):
    """
    递归实现单点更新
    :param i: 需要更新的元素下标
    :param val: 新的值
    :param index: 当前节点在线段树数组中的下标
    :param left: 当前节点管理的区间左端点
    :param right: 当前节点管理的区间右端点
    """
    # 如果到达叶子节点，直接更新节点值
    if self.tree[index].left == self.tree[index].right:
        self.tree[index].val = val  # 叶子节点，节点值修改为 val
        return

    mid = left + (right - left) // 2  # 计算区间中点
    left_index = index * 2 + 1        # 左子节点的下标
    right_index = index * 2 + 2       # 右子节点的下标

    # 判断 i 属于左子树还是右子树，递归更新
    if i <= mid:
        self.__update_point(i, val, left_index, left, mid)  # 在左子树中更新
    else:
        self.__update_point(i, val, right_index, mid + 1, right)  # 在右子树中更新

    self.__pushup(index)  # 向上更新当前节点的区间值

3.2 区间查询

区间查询：即查询区间 $[q\_left, q\_right]$ 上的区间聚合值（如区间和、区间最值等）。

区间查询通常采用递归方式实现，具体流程如下：

1. 如果查询区间 $[q\_left, q\_right]$ 完全覆盖当前节点区间 $[left, right]$（即 $left \ge q\_left$ 且 $right \le q\_right$），直接返回该节点的区间值。
2. 如果查询区间 $[q\_left, q\_right]$ 与当前节点区间 $[left, right]$ 无交集（即 $right < q\_left$ 或 $left > q\_right$），返回 $0$（或聚合运算的单位元）。
3. 如果两区间有交集，则递归查询左右子区间，并将结果合并：
   • 如果 $q\_left \le mid$，递归查询左子区间 $[left, mid]$，记为 $res\_left$。
   • 如果 $q\_right > mid$，递归查询右子区间 $[mid+1, right]$，记为 $res\_right$。
   • 最终返回 $res\_left$ 与 $res\_right$ 的聚合结果。

线段树区间查询的代码如下：

# 区间查询，查询区间 [q_left, q_right] 的区间聚合值
def query_interval(self, q_left, q_right):
    """
    查询区间 [q_left, q_right] 的区间聚合值（如区间和、区间最值等）

    :param q_left: 查询区间左端点
    :param q_right: 查询区间右端点
    :return: 区间 [q_left, q_right] 的聚合值
    """
    return self.__query_interval(q_left, q_right, 0, 0, self.size - 1)

# 区间查询的递归实现
def __query_interval(self, q_left, q_right, index, left, right):
    """
    递归查询线段树节点 [left, right] 区间与查询区间 [q_left, q_right] 的交集部分的聚合值

    :param q_left: 查询区间左端点
    :param q_right: 查询区间右端点
    :param index: 当前节点在线段树数组中的下标
    :param left: 当前节点管理的区间左端点
    :param right: 当前节点管理的区间右端点
    :return: 区间 [q_left, q_right] 与 [left, right] 的交集部分的聚合值
    """
    # 情况 1：当前节点区间被查询区间完全覆盖，直接返回节点值
    if left >= q_left and right <= q_right:
        return self.tree[index].val
    # 情况 2：当前节点区间与查询区间无交集，返回单位元（如区间和为 0，区间最小值为正无穷等）
    if right < q_left or left > q_right:
        return 0

    # 情况 3：当前节点区间与查询区间有部分重叠，递归查询左右子区间
    self.__pushdown(index)  # 下推懒惰标记，保证子节点信息正确

    mid = left + (right - left) // 2        # 计算区间中点
    left_index = index * 2 + 1              # 左子节点下标
    right_index = index * 2 + 2             # 右子节点下标
    res_left = 0                            # 左子树查询结果初始化
    res_right = 0                           # 右子树查询结果初始化
    if q_left <= mid:                       # 查询区间与左子区间有交集
        res_left = self.__query_interval(q_left, q_right, left_index, left, mid)
    if q_right > mid:                       # 查询区间与右子区间有交集
        res_right = self.__query_interval(q_left, q_right, right_index, mid + 1, right)
    return self.function(res_left, res_right)  # 合并左右子树结果并返回

3.3 区间更新

区间更新：即将区间 $[q\_left, q\_right]$ 内所有元素批量修改为 $val$。

3.3.1 延迟标记（懒惰标记）

线段树的区间更新如果每次都递归到所有被覆盖的叶子节点，复杂度会退化为 $O(n)$。为避免无用的重复更新，线段树引入了 延迟标记（懒惰标记）：当某个节点区间 $[left, right]$ 被更新区间 $[q\_left, q\_right]$ 完全覆盖时，只需直接更新该节点的值，并打上延迟标记，表示其子节点尚未被真正更新。只有在后续递归访问到子节点时，才将更新操作「下推」到子节点。

这样，区间更新和区间查询的时间复杂度都能保持 $O(\log_2 n)$。

区间更新的主要步骤如下：

1. 如果 $[q\_left, q\_right]$ 完全覆盖当前节点区间 $[left, right]$，则直接更新当前节点的值，并设置延迟标记。
2. 如果 $[q\_left, q\_right]$ 与 $[left, right]$ 无交集，直接返回。
3. 若有部分重叠，先将当前节点的延迟标记下推到子节点（如果有），然后递归更新左右子区间，最后更新当前节点的值。

3.3.2 下推延迟标记

当节点有延迟标记时，需要将该标记下推到左右子节点，具体做法：

1. 将左子节点的值和懒惰标记更新为 $val$。
2. 将右子节点的值和懒惰标记更新为 $val$。
3. 清除当前节点的懒惰标记。

这样可以保证每个节点的更新操作只在必要时才真正执行，极大提升效率。

3.3.3 区间赋值操作（延迟标记）

使用延迟标记实现区间赋值的代码如下：

def update_interval(self, q_left, q_right, val):
    """
    对区间 [q_left, q_right] 进行区间赋值操作，将该区间内所有元素修改为 val
    """
    self.__update_interval(q_left, q_right, val, 0, 0, self.size - 1)

def __update_interval(self, q_left, q_right, val, index, left, right):
    """
    递归实现区间赋值更新
    参数说明：
        q_left, q_right: 待更新的目标区间
        val: 赋值的目标值
        index: 当前节点在线段树数组中的下标
        left, right: 当前节点所表示的区间范围
    """
    # 情况 1：当前节点区间被 [q_left, q_right] 完全覆盖，直接更新并打懒惰标记
    if left >= q_left and right <= q_right:
        interval_size = (right - left + 1)  # 当前区间长度
        self.tree[index].val = interval_size * val  # 区间所有元素赋值为 val
        self.tree[index].lazy_tag = val             # 打上懒惰标记
        return
    # 情况 2：当前节点区间与 [q_left, q_right] 无交集，直接返回
    if right < q_left or left > q_right:
        return

    # 情况 3：部分重叠，先下推懒惰标记，再递归更新左右子区间
    self.__pushdown(index)

    mid = left + (right - left) // 2            # 区间中点
    left_index = index * 2 + 1                  # 左子节点下标
    right_index = index * 2 + 2                 # 右子节点下标
    if q_left <= mid:                           # 左子区间有交集
        self.__update_interval(q_left, q_right, val, left_index, left, mid)
    if q_right > mid:                           # 右子区间有交集
        self.__update_interval(q_left, q_right, val, right_index, mid + 1, right)

    self.__pushup(index)                        # 回溯时更新当前节点的值


def __pushdown(self, index):
    """
    将当前节点的懒惰标记下推到左右子节点，并更新子节点的值
    """
    lazy_tag = self.tree[index].lazy_tag
    if lazy_tag is None:
        return

    left_index = index * 2 + 1                  # 左子节点下标
    right_index = index * 2 + 2                 # 右子节点下标

    # 更新左子节点的懒惰标记和值
    self.tree[left_index].lazy_tag = lazy_tag
    left_size = self.tree[left_index].right - self.tree[left_index].left + 1
    self.tree[left_index].val = lazy_tag * left_size

    # 更新右子节点的懒惰标记和值
    self.tree[right_index].lazy_tag = lazy_tag
    right_size = self.tree[right_index].right - self.tree[right_index].left + 1
    self.tree[right_index].val = lazy_tag * right_size

    # 清除当前节点的懒惰标记
    self.tree[index].lazy_tag = None

3.3.4 区间加减操作（延迟标记）

有些题目要求将区间 $[q\_left, q\_right]$ 内每个元素在原有基础上增加或减少 $val$，而不是直接赋值为 $val$。

针对这种情况，我们需要重新定义「延迟标记」的含义：即表示当前区间整体增加了 $val$，但该操作尚未下传到子区间。相应地，代码实现也要相应调整以支持区间加减操作的延迟更新。

以下是基于延迟标记的区间加减操作代码：

# 区间更新，将区间 [q_left, q_right] 上的所有元素增加 val
def update_interval(self, q_left, q_right, val):
    """
    对区间 [q_left, q_right] 内的所有元素增加 val
    """
    self.__update_interval(q_left, q_right, val, 0, 0, self.size - 1)

def __update_interval(self, q_left, q_right, val, index, left, right):
    """
    递归实现区间加法更新
    参数:
        q_left, q_right: 待更新的区间范围
        val: 增加的值
        index: 当前节点在线段树数组中的下标
        left, right: 当前节点所表示的区间范围
    """
    # 情况 1：当前节点区间被 [q_left, q_right] 完全覆盖，直接打懒惰标记并更新区间和
    if left >= q_left and right <= q_right:
        interval_size = right - left + 1  # 当前节点区间长度
        if self.tree[index].lazy_tag is not None:
            self.tree[index].lazy_tag += val  # 累加懒惰标记
        else:
            self.tree[index].lazy_tag = val   # 新建懒惰标记
        self.tree[index].val += val * interval_size  # 区间和增加
        return

    # 情况2：当前节点区间与 [q_left, q_right] 无交集，直接返回
    if right < q_left or left > q_right:
        return

    # 情况3：部分重叠，先下推懒惰标记，再递归更新左右子区间
    self.__pushdown(index)

    mid = left + (right - left) // 2
    left_index = index * 2 + 1
    right_index = index * 2 + 2
    if q_left <= mid:
        self.__update_interval(q_left, q_right, val, left_index, left, mid)
    if q_right > mid:
        self.__update_interval(q_left, q_right, val, right_index, mid + 1, right)

    self.__pushup(index)  # 回溯时更新当前节点的区间和

def __pushdown(self, index):
    """
    将当前节点的懒惰标记下推到左右子节点，并同步更新子节点的区间和
    """
    lazy_tag = self.tree[index].lazy_tag
    if lazy_tag is None:
        return

    left_index = index * 2 + 1
    right_index = index * 2 + 2

    # 处理左子节点
    if self.tree[left_index].lazy_tag is not None:
        self.tree[left_index].lazy_tag += lazy_tag
    else:
        self.tree[left_index].lazy_tag = lazy_tag
    left_size = self.tree[left_index].right - self.tree[left_index].left + 1
    self.tree[left_index].val += lazy_tag * left_size

    # 处理右子节点
    if self.tree[right_index].lazy_tag is not None:
        self.tree[right_index].lazy_tag += lazy_tag
    else:
        self.tree[right_index].lazy_tag = lazy_tag
    right_size = self.tree[right_index].right - self.tree[right_index].left + 1
    self.tree[right_index].val += lazy_tag * right_size

    # 清除当前节点的懒惰标记
    self.tree[index].lazy_tag = None

4. 总结

4.1 核心要点

• 线段树通过对区间反复二分，让每个节点维护一个子区间的聚合信息（如和、最值）。
• 使用数组顺序存储，容量通常取约 4 * n，查询/更新沿树高进行。
• 引入懒惰标记后，区间更新无需遍历到所有叶子，保持对数级复杂度。
• 聚合函数可配置（sum/max/min/自定义），需满足可结合性以支持自底向上合并。

4.2 复杂度分析

操作	最优时间	最坏时间	平均时间	空间复杂度	稳定性
构建	O(n)	O(n)	O(n)	O(n)	不涉及
单点更新	O(log n)	O(log n)	O(log n)	O(1)（递归为 O(log n) 栈）	不涉及
区间查询	O(log n)	O(log n)	O(log n)	O(1)（递归为 O(log n) 栈）	不涉及
区间更新（含懒标）	O(log n)	O(log n)	O(log n)	O(1)（递归为 O(log n) 栈）	不涉及

说明：如果不使用懒惰标记，区间更新在最坏情况下会退化为 O(n)。

4.3 算法特点

优点：

• 区间查询与区间更新效率高（均为 O(log n)）。
• 适配多种聚合函数，扩展性强。
• 支持动态数据的在线维护。

缺点：

• 实现复杂度与常数因子较大，代码易错。
• 对聚合函数有约束（需可结合），不适合不可结合的运算。
• 多维线段树实现复杂，内存与常数进一步增大；对于简单前缀和/仅单点更新的场景，树状数组往往更简洁高效。

练习题目

• 线段树题目列表

参考资料

• 【书籍】ACM-ICPC 程序设计系列 - 算法设计与实现 - 陈宇 吴昊 主编
• 【书籍】算法训练营 陈小玉 著
• 【博文】史上最详细的线段树教程 - 知乎
• 【博文】线段树 Segment Tree 实战 - halfrost
• 【博文】线段树 - OI Wiki
• 【博文】线段树的 python 实现 - 年糕的博客 - CSDN博客
• 【博文】线段树 从入门到进阶 - Dijkstra·Liu - 博客园