01. 线段树知识

ITCharge大约 21 分钟

线段树知识

1. 线段树简介

1.1 线段树的定义

线段树（Segment Tree）：一种基于分治思想的二叉树，用于在区间上进行信息统计。它的每一个节点都对应一个区间 $[left, right]$ ， $left$ 、 $right$ 通常是整数。每一个叶子节点表示了一个单位区间（长度为 $1$ ），叶子节点对应区间上 $left == right$ 。每一个非叶子节点 $[left, right]$ 的左子节点表示的区间都为 $[left, (left + right) / 2]$ ，右子节点表示的的区间都为 $[(left + right) / 2 + 1, right]$ 。

线段树是一棵平衡二叉树，树上的每个节点维护一个区间。根节点维护的是整个区间，每个节点维护的是父亲节点的区间二等分之后的其中一个子区间。当有 $n$ 个元素时，对区间的操作（单点更新、区间更新、区间查询等）可以在 $O(\log_2n)$ 的时间复杂度内完成。

如下图所示，这是一棵区间为 $[0, 7]$ 的线段树。

1.2 线段树的特点

根据上述描述，我们可以总结一下线段树的特点：

线段树的每个节点都代表一个区间。
线段树具有唯一的根节点，代表的区间是整个统计范围，比如 $[1, n]$ 。
线段树的每个叶子节点都代表一个长度为 $1$ 的单位区间 $[x, x]$ 。
对于每个内部节点 $[left, right]$ ，它的左子节点是 $[left, mid]$ ，右子节点是 $[mid + 1, right]$ 。其中 $mid = (left + right) / 2$ （向下取整）。

2. 线段树的构建

2.1 线段树的存储结构

之前我们学习过二叉树的两种存储结构，一种是「链式存储结构」，另一种是「顺序存储结构」。线段树也可以使用这两种存储结构来实现。

由于线段树近乎是完全二叉树，所以很适合用「顺序存储结构」来实现。

我们可以采用与完全二叉树类似的编号方法来对线段树进行编号，方法如下：

根节点的编号为 $0$ 。
如果某二叉树节点（非叶子节点）的下标为 $i$ ，那么其左孩子节点下标为 $2 \times i + 1$ ，右孩子节点下标为 $2 \times i + 2$ 。
如果某二叉树节点（非根节点）的下标为 $i$ ，那么其父节点下标为 $(i - 1) // 2$ ， $//$ 表示整除。

这样我们就能使用一个数组来保存线段树。那么这个数组的大小应该设置为多少才合适？

在理想情况下， $n$ 个单位区间构成的线段树是一棵满二叉树，节点数为 $n + n/2 + n/4 + ... + 2 + 1 = 2 \times n - 1$ 个。因为 $2 \times n - 1 < 2 \times n$ ，所以在理想情况下，只需要使用一个大小为 $2 \times n$ 的数组来存储线段树就足够了。
但是在一般情况下，有些区间元素需要开辟新的一层来存储元素。线段树的深度为 $\lceil \log_2n \rceil$ ，最坏情况下叶子节点（包括无用的节点）的数量为 $2^{\lceil \log_2n \rceil}$ 个，总节点数为 $2^{\lceil \log_2n \rceil + 1} - 1$ 个，可以近似看做是 $4 * n$ ，所以我们可以使用一个大小为 $4 \times n$ 的数组来存储线段树。

2.2 线段树的构建方法

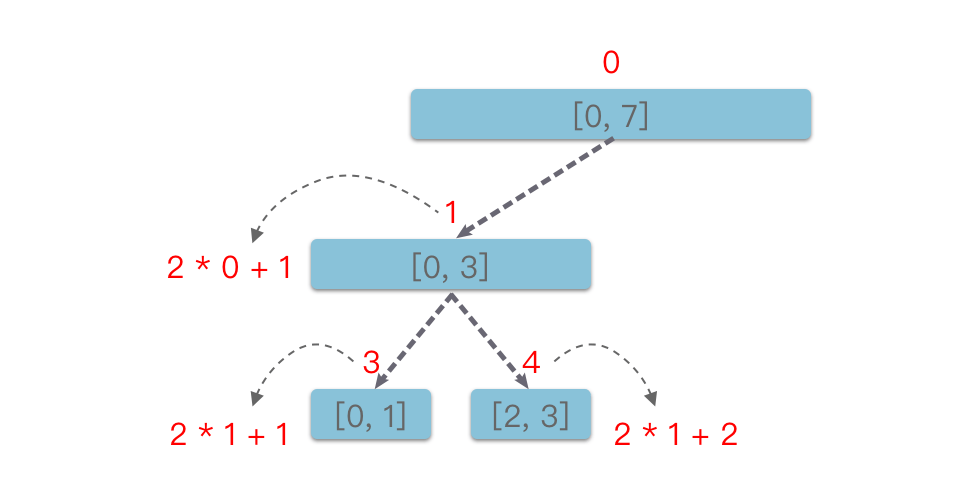
通过上图可知：下标为 $i$ 的节点的孩子节点下标为 $2 \times i + 1$ 和 $2 \times i + 2$ 。所以线段树十分适合采用递归的方法来创建。具体步骤如下：

如果是叶子节点（ $left == right$ ），则节点的值就是对应位置的元素值。
如果是非叶子节点，则递归创建左子树和右子树。
节点的区间值（区间和、区间最大值、区间最小值）等于该节点左右子节点元素值的对应计算结果。

线段树的构建实现代码如下：

# 线段树的节点类
class TreeNode:
    def __init__(self, val=0):
        self.left = -1                              # 区间左边界
        self.right = -1                             # 区间右边界
        self.val = val                              # 节点值（区间值）
        self.lazy_tag = None                        # 区间和问题的延迟更新标记
        
        
# 线段树类
class SegmentTree:
    def __init__(self, nums, function):
        self.size = len(nums)
        self.tree = [TreeNode() for _ in range(4 * self.size)]  # 维护 TreeNode 数组
        self.nums = nums                            # 原始数据
        self.function = function                    # function 是一个函数，左右区间的聚合方法
        if self.size > 0:
            self.__build(0, 0, self.size - 1)
            
    # 构建线段树，节点的存储下标为 index，节点的区间为 [left, right]
    def __build(self, index, left, right):
        self.tree[index].left = left
        self.tree[index].right = right
        if left == right:                           # 叶子节点，节点值为对应位置的元素值
            self.tree[index].val = self.nums[left]
            return
    
        mid = left + (right - left) // 2            # 左右节点划分点
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        self.__build(left_index, left, mid)         # 递归创建左子树
        self.__build(right_index, mid + 1, right)   # 递归创建右子树
        self.__pushup(index)                        # 向上更新节点的区间值
    
    # 向上更新下标为 index 的节点区间值，节点的区间值等于该节点左右子节点元素值的聚合计算结果
    def __pushup(self, index):
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        self.tree[index].val = self.function(self.tree[left_index].val, self.tree[right_index].val)

这里的 function 指的是线段树区间合并的聚合方法。可以根据题意进行变化，常见的操作有求和、取最大值、取最小值等等。

3. 线段树的基本操作

线段树的基本操作主要涉及到单点更新、区间查询和区间更新操作。下面我们来进行一一讲解。

3.1 线段树的单点更新

线段树的单点更新：修改一个元素的值，例如将 $nums[i]$ 修改为 $val$ 。

我们可以采用递归的方式进行单点更新，具体步骤如下：

如果是叶子节点，满足 $left == right$ ，则更新该节点的值。
如果是非叶子节点，则判断应该在左子树中更新，还是应该在右子树中更新。
在对应的左子树或右子树中更新节点值。
左右子树更新返回之后，向上更新节点的区间值（区间和、区间最大值、区间最小值等），区间值等于该节点左右子节点元素值的聚合计算结果。

线段树的单点更新实现代码如下：

    # 单点更新，将 nums[i] 更改为 val
    def update_point(self, i, val):
        self.nums[i] = val
        self.__update_point(i, val, 0, 0, self.size - 1)
        
    # 单点更新，将 nums[i] 更改为 val。节点的存储下标为 index，节点的区间为 [left, right]
    def __update_point(self, i, val, index, left, right):
        if self.tree[index].left == self.tree[index].right:
            self.tree[index].val = val              # 叶子节点，节点值修改为 val
            return
        
        mid = left + (right - left) // 2            # 左右节点划分点
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        if i <= mid:                                # 在左子树中更新节点值
            self.__update_point(i, val, left_index, left, mid)
        else:                                       # 在右子树中更新节点值
            self.__update_point(i, val, right_index, mid + 1, right)
        self.__pushup(index)                        # 向上更新节点的区间值

3.2 线段树的区间查询

线段树的区间查询：查询一个区间为 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 的区间值。

我们可以采用递归的方式进行区间查询，具体步骤如下：

如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 完全覆盖了当前节点所在区间 $[left, right]$ ，即 $left \ge q\underline{\hspace{0.5em}}left$ 并且 $right \le q\underline{\hspace{0.5em}}right$ ，则返回该节点的区间值。
如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 与当前节点所在区间 $[left, right]$ 毫无关系，即 $right < q\underline{\hspace{0.5em}}left$ 或者 $left > q\underline{\hspace{0.5em}}right$ ，则返回 $0$ 。
如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ $[q l e f t, q r i g h t]$ 与当前节点所在区间有交集，则：
1. 如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 与左子节点所在区间 $[left, mid]$ 有交集，即 $q\underline{\hspace{0.5em}}left \le mid$ ，则在当前节点的左子树中进行查询并保存查询结果 $res_\underline{\hspace{0.5em}}left$ 。
2. 如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 与右子节点所在区间 $[mid + 1, right]$ 有交集，即 $q\underline{\hspace{0.5em}}right > mid$ ，则在当前节点的右子树中进行查询并保存查询结果 $res_\underline{\hspace{0.5em}}right$ 。
3. 最后返回左右子树元素区间值的聚合计算结果。

线段树的区间查询代码如下：

    # 区间查询，查询区间为 [q_left, q_right] 的区间值
    def query_interval(self, q_left, q_right):
        return self.__query_interval(q_left, q_right, 0, 0, self.size - 1)
    
    # 区间查询，在线段树的 [left, right] 区间范围中搜索区间为 [q_left, q_right] 的区间值
    def __query_interval(self, q_left, q_right, index, left, right):
        if left >= q_left and right <= q_right:     # 节点所在区间被 [q_left, q_right] 所覆盖
            return self.tree[index].val             # 直接返回节点值
        if right < q_left or left > q_right:        # 节点所在区间与 [q_left, q_right] 无关
            return 0
    
        self.__pushdown(index)
    
        mid = left + (right - left) // 2            # 左右节点划分点
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        res_left = 0                                # 左子树查询结果
        res_right = 0                               # 右子树查询结果
        if q_left <= mid:                           # 在左子树中查询
            res_left = self.__query_interval(q_left, q_right, left_index, left, mid)
        if q_right > mid:                           # 在右子树中查询
            res_right = self.__query_interval(q_left, q_right, right_index, mid + 1, right)
        return self.function(res_left, res_right)   # 返回左右子树元素值的聚合计算结果

3.3 线段树的区间更新

线段树的区间更新：对 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 区间进行更新，例如将 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 区间内所有元素都更新为 $val$ 。

3.3.1 延迟标记

线段树在进行单点更新、区间查询时，区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 在线段树上会被分成 $O(\log_2n)$ 个小区间（节点），从而在 $O(\log_2n)$ 的时间复杂度内完成操作。

而在「区间更新」操作中，如果某个节点区间 $[left, right]$ 被修改区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 完全覆盖，则以该节点为根的整棵子树中所有节点的区间值都要发生变化，如果逐一进行更新的话，将使得一次区间更新操作的时间复杂度增加到 $O(n)$ 。

设想这一种情况：如果我们在一次执行更新操作时，发现当前节点区间 $[left, right]$ 被修改区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 完全覆盖，然后逐一更新了区间 $[left, right]$ 对应子树中的所有节点，但是在后续的区间查询操作中却根本没有用到 $[left, right]$ 作为候选答案，则更新 $[left, right]$ 对应子树的工作就是徒劳的。

如果我们减少更新的次数和时间复杂度，应该怎么办？

我们可以向线段树的节点类中增加一个 「延迟标记」，标识为 「该区间曾经被修改为 $val$ ，但其子节点区间值尚未更新」。也就是说除了在进行区间更新时，将区间子节点的更新操作延迟到 「在后续操作中递归进入子节点时」 再执行。这样一来，每次区间更新和区间查询的时间复杂度都降低到了 $O(\log_2n)$ 。

使用「延迟标记」的区间更新步骤为：

如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 完全覆盖了当前节点所在区间 $[left, right]$ ，即 $left \ge q\underline{\hspace{0.5em}}left$ 并且 $right \le q\underline{\hspace{0.5em}}right$ ，则更新当前节点所在区间的值，并将当前节点的延迟标记为区间值。
如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 与当前节点所在区间 $[left, right]$ 毫无关系，即 $right < q\underline{\hspace{0.5em}}left$ 或者 $left > q\underline{\hspace{0.5em}}right$ ，则直接返回。
如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ $[q l e f t, q r i g h t]$ 与当前节点所在区间有交集，则：
1. 如果当前节点使用了「延迟标记」，即延迟标记不为 $None$ ，则将当前区间的更新操作应用到该节点的子节点上（即向下更新）。
2. 如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 与左子节点所在区间 $[left, mid]$ 有交集，即 $q\underline{\hspace{0.5em}}left \le mid$ ，则在当前节点的左子树中更新区间值。
3. 如果区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 与右子节点所在区间 $[mid + 1, right]$ 有交集，即 $q\underline{\hspace{0.5em}}right > mid$ ，则在当前节点的右子树中更新区间值。
4. 左右子树更新返回之后，向上更新节点的区间值（区间和、区间最大值、区间最小值），区间值等于该节点左右子节点元素值的对应计算结果。

3.3.2 向下更新

上面提到了如果当前节点使用了「延迟标记」，即延迟标记不为 $None$ ，则将当前区间的更新操作应用到该节点的子节点上（即向下更新）。这里描述一下向下更新的具体步骤：

更新左子节点值和左子节点懒惰标记为 $val$ 。
更新右子节点值和右子节点懒惰标记为 $val$ 。
将当前节点的懒惰标记更新为 $None$ 。

使用「延迟标记」的区间更新实现代码如下：

    # 区间更新，将区间为 [q_left, q_right] 上的元素值修改为 val
    def update_interval(self, q_left, q_right, val):
        self.__update_interval(q_left, q_right, val, 0, 0, self.size - 1)
        
    # 区间更新
    def __update_interval(self, q_left, q_right, val, index, left, right):
        
        if left >= q_left and right <= q_right:     # 节点所在区间被 [q_left, q_right] 所覆盖
            interval_size = (right - left + 1)      # 当前节点所在区间大小
            self.tree[index].val = interval_size * val # 当前节点所在区间每个元素值改为 val
            self.tree[index].lazy_tag = val         # 将当前节点的延迟标记为区间值
            return
        if right < q_left or left > q_right:        # 节点所在区间与 [q_left, q_right] 无关
            return 0
    
        self.__pushdown(index)
    
        mid = left + (right - left) // 2            # 左右节点划分点
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        if q_left <= mid:                           # 在左子树中更新区间值
            self.__update_interval(q_left, q_right, val, left_index, left, mid)
        if q_right > mid:                           # 在右子树中更新区间值
            self.__update_interval(q_left, q_right, val, right_index, mid + 1, right)
        
        self.__pushup(index)
    
    # 向下更新下标为 index 的节点所在区间的左右子节点的值和懒惰标记
    def __pushdown(self, index):
        lazy_tag = self.tree[index].lazy_tag
        if not lazy_tag:
            return
        
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        
        self.tree[left_index].lazy_tag = lazy_tag   # 更新左子节点懒惰标记
        left_size = (self.tree[left_index].right - self.tree[left_index].left + 1)
        self.tree[left_index].val = lazy_tag * left_size    # 更新左子节点值

        self.tree[right_index].lazy_tag = lazy_tag  # 更新右子节点懒惰标记
        right_size = (self.tree[right_index].right - self.tree[right_index].left + 1)
        self.tree[right_index].val = lazy_tag * right_size  # 更新右子节点值

        self.tree[index].lazy_tag = None            # 更新当前节点的懒惰标记

注意：有些题目中不是将 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 区间更新为 $val$ ，而是将 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 区间中每一个元素值在原值基础增加或减去 $val$ 。
对于这种情况，我们可以更改一下「延迟标记」的定义。改变为： 「该区间曾经变化了 $val$ ，但其子节点区间值尚未更新」。并更改对应的代码逻辑。

使用「延迟标记」的区间增减更新实现代码如下：

    # 区间更新，将区间为 [q_left, q_right] 上的元素值修改为 val
    def update_interval(self, q_left, q_right, val):
        self.__update_interval(q_left, q_right, val, 0, 0, self.size - 1)
        
    # 区间更新
    def __update_interval(self, q_left, q_right, val, index, left, right):
        
        if left >= q_left and right <= q_right:     # 节点所在区间被 [q_left, q_right] 所覆盖
#            interval_size = (right - left + 1)      # 当前节点所在区间大小
#            self.tree[index].val = interval_size * val # 当前节点所在区间每个元素值改为 val
#            self.tree[index].lazy_tag = val         # 将当前节点的延迟标记为区间值
        
            if self.tree[index].lazy_tag:
                self.tree[index].lazy_tag += val    # 将当前节点的延迟标记增加 val
            else:
                self.tree[index].lazy_tag = val     # 将当前节点的延迟标记增加 val
            interval_size = (right - left + 1)      # 当前节点所在区间大小
            self.tree[index].val += val * interval_size  # 当前节点所在区间每个元素值增加 val
            return
        if right < q_left or left > q_right:        # 节点所在区间与 [q_left, q_right] 无关
            return 0
    
        self.__pushdown(index)
    
        mid = left + (right - left) // 2            # 左右节点划分点
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        if q_left <= mid:                           # 在左子树中更新区间值
            self.__update_interval(q_left, q_right, val, left_index, left, mid)
        if q_right > mid:                           # 在右子树中更新区间值
            self.__update_interval(q_left, q_right, val, right_index, mid + 1, right)
        
        self.__pushup(index)
    
    # 向下更新下标为 index 的节点所在区间的左右子节点的值和懒惰标记
    def __pushdown(self, index):
        lazy_tag = self.tree[index].lazy_tag
        if not lazy_tag:
            return
        
        left_index = index * 2 + 1                  # 左子节点的存储下标
        right_index = index * 2 + 2                 # 右子节点的存储下标
        
        if self.tree[left_index].lazy_tag:
            self.tree[left_index].lazy_tag += lazy_tag  # 更新左子节点懒惰标记
        else:
            self.tree[left_index].lazy_tag = lazy_tag
        left_size = (self.tree[left_index].right - self.tree[left_index].left + 1)
        self.tree[left_index].val += lazy_tag * left_size   # 左子节点每个元素值增加 lazy_tag
        
        if self.tree[right_index].lazy_tag:
            self.tree[right_index].lazy_tag += lazy_tag # 更新右子节点懒惰标记
        else:
            self.tree[right_index].lazy_tag = lazy_tag
        right_size = (self.tree[right_index].right - self.tree[right_index].left + 1)
        self.tree[right_index].val += lazy_tag * right_size # 右子节点每个元素值增加 lazy_tag
        
        self.tree[index].lazy_tag = None            # 更新当前节点的懒惰标记

4. 线段树的常见题型

4.1 RMQ 问题

RMQ 问题：Range Maximum / Minimum Query 的缩写，指的是对于长度为 $n$ 的数组序列 $nums$ ，回答若干个询问问题 RMQ(nums, q_left, q_right)，要求返回数组序列 $nums$ 在区间 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 中的最大（最小）值。也就是求区间最大（最小）值问题。

假设查询次数为 $q$ ，则使用朴素算法解决 RMQ 问题的时间复杂度为 $O(q \times n)$ 。而使用线段树解决 RMQ 问题的时间复杂度为 $O(q \times n) \sim Q(q \times \log_2n)$ 之间。

4.2 单点更新，区间查询问题

单点更新，区间查询问题：
修改某一个元素的值。
查询区间为 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 的区间值。

这类问题直接使用「3.1 线段树的单点更新」和「3.2 线段树的区间查询」即可解决。

4.3 区间更新，区间查询问题

区间更新，区间查询问题：
修改某一个区间的值。
查询区间为 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 的区间值。

这类问题直接使用「3.3 线段树的区间更新」和「3.2 线段树的区间查询」即可解决。

4.4 区间合并问题

区间合并，区间查询问题：
修改某一个区间的值。
查询区间为 $[q\underline{\hspace{0.5em}}left, q\underline{\hspace{0.5em}}right]$ 中满足条件的连续最长区间值。

这类问题需要在「3.3 线段树的区间更新」和「3.2 线段树的区间查询」的基础上增加变动，在进行向上更新时需要对左右子节点的区间进行合并。

4.5 扫描线问题

扫描线问题：虚拟扫描线或扫描面来解决欧几里德空间中的各种问题，一般被用来解决图形面积，周长等问题。
主要思想为：想象一条线（通常是一条垂直线）在平面上扫过或移动，在某些点停止。几何操作仅限于几何对象，无论何时停止，它们都与扫描线相交或紧邻扫描线，并且一旦线穿过所有对象，就可以获得完整的解。

这类问题通常坐标跨度很大，需要先对每条扫描线的坐标进行离散化处理，将 $y$ 坐标映射到 $0, 1, 2, ...$ 中。然后将每条竖线的端点作为区间范围，使用线段树存储每条竖线的信息（ $x$ 坐标、是左竖线还是右竖线等），然后再进行区间合并，并统计相关信息。

5. 线段树的拓展

5.1 动态开点线段树

在有些情况下，线段树需要维护的区间很大（例如 $[1, 10^9]$ ），在实际中用到的节点却很少。

如果使用之前数组形式实现线段树，则需要 $4 \times n$ 大小的空间，空间消耗有点过大了。

这时候我们就可以使用动态开点的思想来构建线段树。

动态开点线段树的算法思想如下：

开始时只建立一个根节点，代表整个区间。
当需要访问线段树的某棵子树（某个子区间）时，再建立代表这个子区间的节点。

动态开点线段树实现代码如下：

# 线段树的节点类
class TreeNode:
    def __init__(self, left=-1, right=-1, val=0):
        self.left = left                            # 区间左边界
        self.right = right                          # 区间右边界
        self.mid = left + (right - left) // 2
        self.leftNode = None                        # 区间左节点
        self.rightNode = None                       # 区间右节点
        self.val = val                              # 节点值（区间值）
        self.lazy_tag = None                        # 区间问题的延迟更新标记
        
        
# 线段树类
class SegmentTree:
    def __init__(self, function):
        self.tree = TreeNode(0, int(1e9))
        self.function = function                    # function 是一个函数，左右区间的聚合方法
            
    # 向上更新 node 节点区间值，节点的区间值等于该节点左右子节点元素值的聚合计算结果
    def __pushup(self, node):
        leftNode = node.leftNode
        rightNode = node.rightNode
        if leftNode and rightNode:
            node.val = self.function(leftNode.val, rightNode.val)
            
    # 单点更新，将 nums[i] 更改为 val
    def update_point(self, i, val):
        self.__update_point(i, val, self.tree)
        
    # 单点更新，将 nums[i] 更改为 val。node 节点的区间为 [node.left, node.right]
    def __update_point(self, i, val, node):
        if node.left == node.right:
            node.val = val                          # 叶子节点，节点值修改为 val
            return
        
        if i <= node.mid:                           # 在左子树中更新节点值
            if not node.leftNode:
                node.leftNode = TreeNode(node.left, node.mid)
            self.__update_point(i, val, node.leftNode)
        else:                                       # 在右子树中更新节点值
            if not node.rightNode:
                node.rightNode = TreeNode(node.mid + 1, node.right)
            self.__update_point(i, val, node.rightNode)
        self.__pushup(node)                         # 向上更新节点的区间值
        
    # 区间查询，查询区间为 [q_left, q_right] 的区间值
    def query_interval(self, q_left, q_right):
        return self.__query_interval(q_left, q_right, self.tree)
    
    # 区间查询，在线段树的 [left, right] 区间范围中搜索区间为 [q_left, q_right] 的区间值
    def __query_interval(self, q_left, q_right, node):
        if node.left >= q_left and node.right <= q_right:   # 节点所在区间被 [q_left, q_right] 所覆盖
            return node.val                         # 直接返回节点值
        if node.right < q_left or node.left > q_right:  # 节点所在区间与 [q_left, q_right] 无关
            return 0
                                  
        self.__pushdown(node)                       # 向下更新节点所在区间的左右子节点的值和懒惰标记
        
        res_left = 0                                # 左子树查询结果
        res_right = 0                               # 右子树查询结果
        if q_left <= node.mid:                      # 在左子树中查询
            if not node.leftNode:
                node.leftNode = TreeNode(node.left, node.mid)
            res_left = self.__query_interval(q_left, q_right, node.leftNode)
        if q_right > node.mid:                      # 在右子树中查询
            if not node.rightNode:
                node.rightNode = TreeNode(node.mid + 1, node.right)
            res_right = self.__query_interval(q_left, q_right, node.rightNode)
        return self.function(res_left, res_right)   # 返回左右子树元素值的聚合计算结果
    
    # 区间更新，将区间为 [q_left, q_right] 上的元素值修改为 val
    def update_interval(self, q_left, q_right, val):
        self.__update_interval(q_left, q_right, val, self.tree)
        
    # 区间更新
    def __update_interval(self, q_left, q_right, val, node):
        if node.left >= q_left and node.right <= q_right:  # 节点所在区间被 [q_left, q_right] 所覆盖
            if node.lazy_tag:
                node.lazy_tag += val                # 将当前节点的延迟标记增加 val
            else:
                node.lazy_tag = val                 # 将当前节点的延迟标记增加 val
            interval_size = (node.right - node.left + 1)    # 当前节点所在区间大小
            node.val += val * interval_size         # 当前节点所在区间每个元素值增加 val
            return
        if node.right < q_left or node.left > q_right:  # 节点所在区间与 [q_left, q_right] 无关
            return 0
    
        self.__pushdown(node)                       # 向下更新节点所在区间的左右子节点的值和懒惰标记
    
        if q_left <= node.mid:                      # 在左子树中更新区间值
            if not node.leftNode:
                node.leftNode = TreeNode(node.left, node.mid)
            self.__update_interval(q_left, q_right, val, node.leftNode)
        if q_right > node.mid:                      # 在右子树中更新区间值
            if not node.rightNode:
                node.rightNode = TreeNode(node.mid + 1, node.right)
            self.__update_interval(q_left, q_right, val, node.rightNode)
            
        self.__pushup(node)
    
    # 向下更新 node 节点所在区间的左右子节点的值和懒惰标记
    def __pushdown(self, node):
        lazy_tag = node.lazy_tag
        if not node.lazy_tag:
            return
        
        if not node.leftNode:
            node.leftNode = TreeNode(node.left, node.mid)
        if not node.rightNode:
            node.rightNode = TreeNode(node.mid + 1, node.right)
            
        if node.leftNode.lazy_tag:
            node.leftNode.lazy_tag += lazy_tag      # 更新左子节点懒惰标记
        else:
            node.leftNode.lazy_tag = lazy_tag       # 更新左子节点懒惰标记
        left_size = (node.leftNode.right - node.leftNode.left + 1)
        node.leftNode.val += lazy_tag * left_size   # 左子节点每个元素值增加 lazy_tag
        
        if node.rightNode.lazy_tag:
            node.rightNode.lazy_tag += lazy_tag     # 更新右子节点懒惰标记
        else:
            node.rightNode.lazy_tag = lazy_tag      # 更新右子节点懒惰标记
        right_size = (node.rightNode.right - node.rightNode.left + 1)
        node.rightNode.val += lazy_tag * right_size # 右子节点每个元素值增加 lazy_tag
        
        node.lazy_tag = None                        # 更新当前节点的懒惰标记

参考资料

【书籍】ACM-ICPC 程序设计系列 - 算法设计与实现 - 陈宇吴昊主编
【书籍】算法训练营陈小玉著
【博文】史上最详细的线段树教程 - 知乎
【博文】线段树 Segment Tree 实战 - halfrost
【博文】线段树 - OI Wiki
【博文】线段树的 python 实现 - 年糕的博客 - CSDN博客
【博文】线段树从入门到进阶 - Dijkstra·Liu - 博客园