7.2 递归算法

ITCharge大约 12 分钟

7.2 递归算法

---

1. 递归简介

递归（Recursion）：是一种将复杂问题分解为与原问题结构相同的子问题，并通过重复求解这些子问题来获得最终解答的方法。在大多数编程语言中，递归通常通过函数自身的调用来实现。

以阶乘为例，数学定义如下：

fact(n) = \begin{cases} 1 & \text{n = 0} \cr n \times fact(n - 1) & \text{n > 0} \end{cases}

我们可以直接用调用函数自身的方式实现阶乘函数 $fact(n)$ ，代码如下：

def fact(n):
    # 递归终止条件：当 n 等于 0 时，返回 1
    if n == 0:
        return 1
    # 递归调用：n 乘以 fact(n - 1)，将问题规模缩小
    return n * fact(n - 1)

以 $n = 6$ 为例，阶乘函数 $fact(6)$ 的递归计算步骤如下：

fact(6)
= 6 * fact(5)
= 6 * (5 * fact(4))
= 6 * (5 * (4 * fact(3)))
= 6 * (5 * (4 * (3 * fact(2))))
= 6 * (5 * (4 * (3 * (2 * fact(1)))))
= 6 * (5 * (4 * (3 * (2 * (1 * fact(0))))))
= 6 * (5 * (4 * (3 * (2 * (1 * 1)))))
= 6 * (5 * (4 * (3 * (2 * 1))))
= 6 * (5 * (4 * (3 * 2)))
= 6 * (5 * (4 * 6))
= 6 * (5 * 24)
= 6 * 120
= 720

上述例子可以用如下方式描述递归的执行过程：

从 $fact(6)$ 开始，函数不断递归调用自身，依次进入 $fact(5)$ 、 $fact(4)$ 、……，直到到达最底层的 $fact(0)$ 。
当 $n == 0$ 时， $fact(0)$ 满足终止条件，直接返回 $1$ ，递归不再继续向下。
返回阶段，从 $fact(0)$ $f a c t (0)$ 开始逐层向上，每一层利用下一层的返回值进行计算：
- $fact(1)$ ：通过 $fact(0)$ 的结果 $1$ ，计算 $fact(1) = 1 \times 1 = 1$ ，返回 $1$ 。
- $fact(2)$ ：通过 $fact(1)$ 的结果 $1$ ，计算 $fact(2) = 2 \times 1 = 2$ ，返回 $2$ 。
- $fact(3)$ ：通过 $fact(2)$ 的结果 $2$ ，计算 $fact(3) = 3 \times 2 = 6$ ，返回 $6$ 。
- $fact(4)$ ：通过 $fact(3)$ 的结果 $6$ ，计算 $fact(4) = 4 \times 6 = 24$ ，返回 $24$ 。
- $fact(5)$ ：通过 $fact(4)$ 的结果 $24$ ，计算 $fact(5) = 5 \times 24 = 120$ ，返回 $120$ 。
- $fact(6)$ ：通过 $fact(5)$ 的结果 $120$ ，计算 $fact(6) = 6 \times 120 = 720$ ，最终返回 $720$ 。

整个递归过程分为两步：

向下递推：不断分解问题，直到满足终止条件（ $n == 0$ ）。
向上回归：逐层返回结果，最终得到原问题的解（即返回 $fact(6) == 720$ ）。

如下图所示：

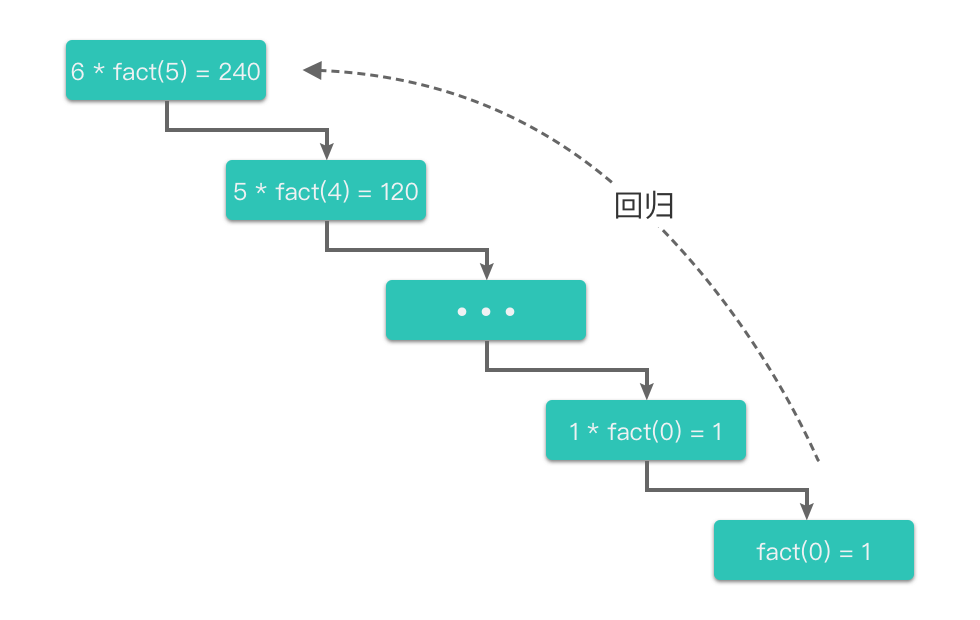
简而言之，递归包含「递推过程」和「回归过程」：

递推过程：将大问题逐步分解为更小的同类子问题，直到终止条件。
回归过程：从最小子问题开始，逐层返回结果，最终解决原问题。

递归的核心思想就是：把大问题拆解为小问题，逐步解决。 因为每一层的处理方式相同，所以递归函数会调用自身，这正是递归的本质。

2. 递归与数学归纳法

递归的本质与「数学归纳法」高度契合。我们先简要回顾数学归纳法的基本步骤：

基础情形：证明当 $n = b$ （ $b$ 通常为 $0$ 或 $1$ ）时，命题成立。
归纳步骤：假设当 $n = k$ 时命题成立，进一步证明 $n = k + 1$ 时命题也成立。这里的关键是利用 $n = k$ 成立的假设，推导出 $n = k + 1$ 也成立。

完成上述两步后，即可得出：对于所有 $n \ge b$ ，命题均成立。

将递归与数学归纳法对应起来，可以这样理解：

递归终止条件：对应于数学归纳法的基础情形（ $n = b$ ），此时直接给出结果。
递推过程：对应于归纳假设部分（假设 $n = k$ 时成立），即假设我们已经知道了规模更小的问题的解。
回归过程：对应于归纳推导部分（由 $n = k$ 推出 $n = k + 1$ ），即利用子问题的解，推导出当前问题的解。

正因为数学归纳法的推理方式与递归的分解和回归过程一致，所以在解决如阶乘、前 $n$ 项和、斐波那契数列等问题时，递归算法往往是最自然的选择。

3. 递归三步法

递归的核心思想是：把大问题拆解为小问题，逐步解决。写递归时，可以遵循以下三步：

写递推公式：找出原问题与子问题的关系，写出递推公式。
确定终止条件：明确递归何时结束，以及结束时的返回值。
翻译为代码：
- 定义递归函数（明确参数和返回值含义）
- 编写递归主体（递推公式对应的递归调用）
- 加入终止条件的判断和处理

3.1 写递推公式

递归的关键在于：将原问题拆解为更小、结构相同的子问题，并用递推公式加以表达。例如，阶乘问题的递推公式为 $fact(n) = n \times fact(n - 1)$ 。

在思考递归时，无需把每一层的递推和回归过程都在脑海中推演到底，否则容易陷入细节而感到困惑。以阶乘为例，它只需分解为一个子问题，因此递归的每一步都容易理解和实现。

但当一个问题需要分解为多个子问题时，逐层推演每一步的递推和回归过程就会变得复杂且难以理清。

此时，推荐的思考方式是：假设所有子问题（如 $B$ 、 $C$ 、 $D$ ）都已经解决，我们只需思考如何利用这些子问题的解来解决原问题 $A$ 。无需再深入每个子问题的内部递归细节，这样可以大大简化思考难度。

实际上，从原问题 $A$ 拆解为子问题 $B$ 、 $C$ 、 $D$ 的过程，就是递归的「递推过程」；而将子问题的解合并为原问题的解，则是「回归过程」。只要明确了如何划分子问题，以及如何通过子问题的解来解决原问题，就能顺利写出递推公式。

因此，编写递归时，重点关注原问题与子问题之间的关系，并据此写出递推公式即可。

3.2 明确终止条件

递归必须有终止条件（递归出口），否则会无限递归导致程序崩溃。终止条件通常是问题的边界值，并在此时直接给出答案。例如， $fact(0) = 1$ ， $f(1) = 1$ 。

3.3 翻译为代码

将递推公式和终止条件转化为代码，通常分为三步：

定义递归函数：明确参数和返回值的含义。
编写递归主体：根据递推公式递归调用自身。
加入终止条件：用条件语句判断并处理终止情况。

综合上述步骤，递归伪代码如下：

def recursion(大规模问题):
    if 递归终止条件:
        递归终止时的处理方法
    
    return recursion(小规模问题)

4. 递归的注意事项

4.1 避免栈溢出

递归在程序执行时依赖于调用栈。每递归调用一次，系统会为该调用分配一个新的栈帧；每当递归返回时，栈帧被销毁。由于系统栈空间有限，如果递归层数过深，极易导致栈溢出（Stack Overflow）。

为降低栈溢出的风险，可以在代码中人为设置递归的最大深度（如 100 层），超过后直接返回错误或采取其他处理措施。但这种方式并不能彻底杜绝栈溢出，因为系统允许的最大递归深度受限于当前可用栈空间，且难以精确预估。

如果递归深度不可控或递归算法难以避免栈溢出，建议将递归改写为非递归（迭代）算法，即用循环和显式栈模拟递归过程，从根本上解决栈空间受限的问题。

4.2 避免重复运算

递归算法常常会遇到重复计算的问题，尤其是在分治结构中多个子问题重叠时。例如，斐波那契数列的递归定义如下：

f(n) = \begin{cases} 0 & n = 0 \\ 1 & n = 1 \\ f(n-1) + f(n-2) & n > 1 \end{cases}

如下图所示，计算 $f(5)$ 时， $f(3)$ 会被多次递归计算， $f(2)$ 、 $f(1)$ 、 $f(0)$ 也会被重复计算，导致效率极低。

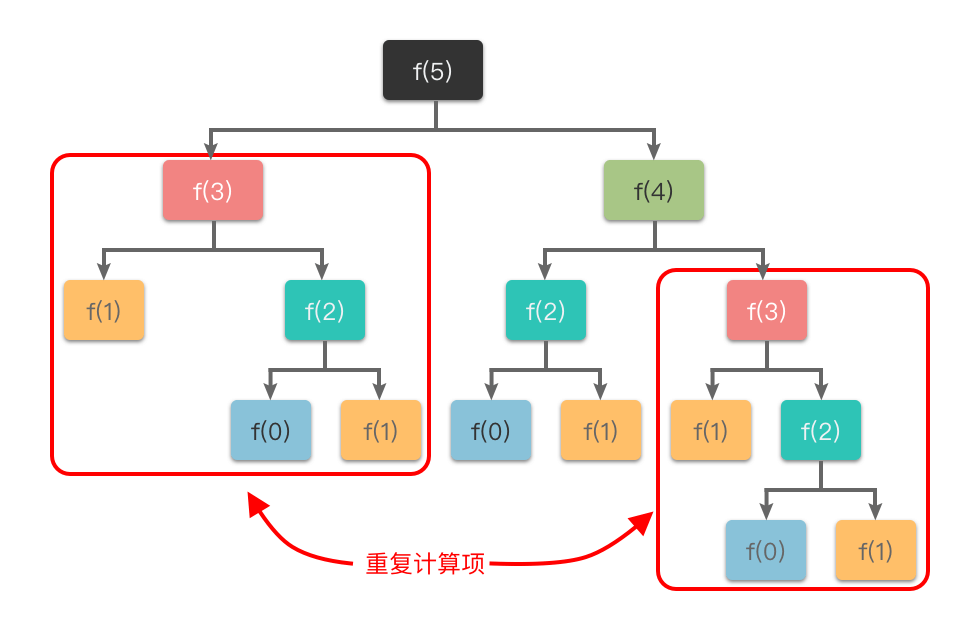
为避免重复运算，可以引入缓存机制（如哈希表、数组或集合）记录已经计算过的子问题结果。这种做法称为「记忆化递归」或「递归 + 备忘录」，也是动态规划的核心思想之一。每次递归调用前，先检查缓存中是否已有结果，若有则直接返回，无需再次递归，从而显著提升效率。

509. 斐波那契数 - 力扣（LeetCode）

5.1.2 题目大意

描述：给定一个整数 $n$ 。

要求：计算第 $n$ 个斐波那契数。

说明：

斐波那契数列的定义如下：
- $f(0) = 0, f(1) = 1$ 。
- $f(n) = f(n - 1) + f(n - 2)$ ，其中 $n > 1$ 。

示例：

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

5.1.3 解题思路

思路 1：递归算法

按照递归解题的「三步走」策略，可以将斐波那契数列问题的递归实现过程梳理如下：

写递推公式： $f(n) = f(n - 1) + f(n - 2)$ 。
确定终止条件： $f(0) = 0$ ， $f(1) = 1$ 。
翻译为代码：
1. 定义递归函数 fib(self, n)，其中 $n$ 表示问题规模，返回第 $n$ 个斐波那契数。
2. 递归主体为：return self.fib(n - 1) + self.fib(n - 2)。
3. 递归终止条件：
  - if n == 0: return 0
  - if n == 1: return 1

思路 1：代码

class Solution:
    def fib(self, n: int) -> int:
        if n == 0:
            return 0
        if n == 1:
            return 1
        return self.fib(n - 1) + self.fib(n - 2)

思路 1：复杂度分析

时间复杂度： $O((\frac{1 + \sqrt{5}}{2})^n)$ 。具体证明方法参考递归求斐波那契数列的时间复杂度，不要被网上的答案误导了 - 知乎。
空间复杂度： $O(n)$ 。每次递归的空间复杂度是 $O(1)$ ，调用栈的深度为 $n$ ，所以总的空间复杂度就是 $O(n)$ 。

5.2 经典例题：二叉树的最大深度

5.2.1 题目链接

104. 二叉树的最大深度 - 力扣（LeetCode）

5.2.2 题目大意

描述：给定一个二叉树的根节点 $root$ 。

要求：找出该二叉树的最大深度。

说明：

二叉树的深度：根节点到最远叶子节点的最长路径上的节点数。
叶子节点：没有子节点的节点。

示例：

示例 1：

输入：[3,9,20,null,null,15,7]
对应二叉树
            3
           / \
          9  20
            /  \
           15   7
输出：3
解释：该二叉树的最大深度为 3

5.2.3 解题思路

思路 1：递归算法

按照递归解题的「三步走」策略，整理递归解法如下：

写递推公式：当前二叉树的最大深度 = max(左子树最大深度, 右子树最大深度) + 1。
- 即：递归分别计算左右子树的深度，取较大值后加 1，得到当前节点的深度。
确定终止条件：当当前节点为空（即 root 为 None）时，返回 0。
翻译为代码：
1. 定义递归函数：maxDepth(self, root)，参数为二叉树根节点 $root$ ，返回该树的最大深度。
2. 递归主体：return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1。
3. 终止条件判断：if not root: return 0。

思路 1：代码

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        
        return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1

思路 1：复杂度分析

时间复杂度： $O(n)$ ，其中 $n$ 是二叉树的节点数目。
空间复杂度： $O(n)$ 。递归函数需要用到栈空间，栈空间取决于递归深度，最坏情况下递归深度为 $n$ ，所以空间复杂度为 $O(n)$ 。

6. 总结

递归的本质是将大问题拆成同结构的小问题，先「递推」到底，再「回归」向上合并结果。写递归时只需站在当前层思考：如果更小规模的子问题都已解决，我如何用它们的结果得到当前答案。

它与数学归纳法一一对应：终止条件对应基础情形，递推与回归对应「假设成立 → 推出更大规模成立」。因此，实践上先写清递推关系，再补充明确的递归出口，最后把思路直接翻译成代码即可。

实战中要特别注意两点：其一，递归层数过深可能导致栈溢出，可限制深度或改写为迭代；其二，子问题重叠会造成重复计算，可使用记忆化（缓存）或转为自底向上的动态规划来优化。

递归尤其适合链式、树形与分治类问题，如二叉树深度、DFS 等。建议先保证正确性，再视场景用缓存或迭代 / DP手段优化时间与空间开销。

练习题目

参考资料

【书籍】算法竞赛入门经典：训练指南 - 刘汝佳，陈锋著
【书籍】算法训练营陈小玉著
【书籍】挑战程序设计竞赛第 2 版 - 秋叶拓哉，岩田阳一，北川宜稔著，巫泽俊，庄俊元，李津羽译
【问答】对于递归有没有什么好的理解方法？ - 知乎 - 方应杭
【问答】对于递归有没有什么好的理解方法？ - 知乎 - 老刘
【博文】递归 & 分治 - OI Wiki
【博文】递归详解 - labuladong
【博文】递归 - 数据结构与算法之美 - 极客时间
【视频】清华学长带你从宏观角度看递归

7.2 递归算法

7.2 递归算法

1. 递归简介

2. 递归与数学归纳法

3. 递归三步法

3.1 写递推公式

3.2 明确终止条件

3.3 翻译为代码

4. 递归的注意事项

4.1 避免栈溢出

4.2 避免重复运算

5. 递归的应用

5.1 经典例题：斐波那契数

5.1.1 题目链接

5.1.2 题目大意

5.1.3 解题思路

思路 1：递归算法

思路 1：代码

思路 1：复杂度分析

5.2 经典例题：二叉树的最大深度

5.2.1 题目链接

5.2.2 题目大意

5.2.3 解题思路

思路 1：递归算法

思路 1：代码

思路 1：复杂度分析

6. 总结

练习题目

参考资料