7.3 分治算法

ITCharge大约 9 分钟

7.3 分治算法

---

1. 分治算法简介

1.1 分治算法的定义

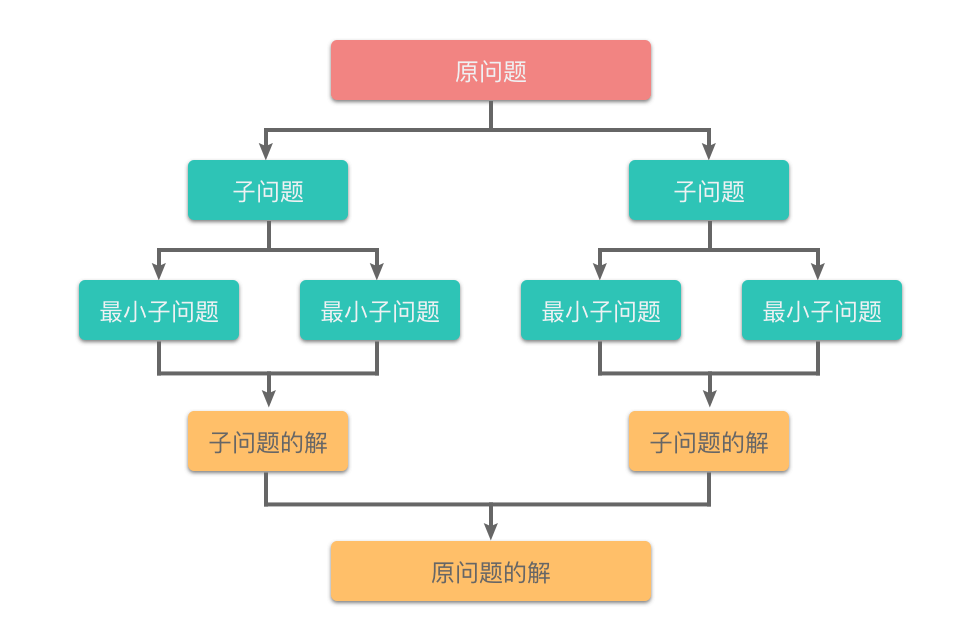
分治算法（Divide and Conquer）：即「分而治之」，把一个复杂问题拆分成多个相同或相似的子问题，递归分解，直到子问题足够简单可以直接解决，最后将子问题的解合并得到原问题的解。

简而言之，分治算法就是：把大问题不断拆小，直到可以直接求解，再合并结果。

1.2 分治算法与递归算法的关系

分治和递归都强调「拆分问题」。递归是一种实现方式，分治是一种思想。可以理解为： $\text{递归算法} \subset \text{分治算法}$ 。

分治算法常用递归实现，也可以用迭代实现。例如：快速傅里叶变换、二分查找、非递归归并排序等。

下面先介绍分治算法的适用条件，再讲基本步骤。

1.3 分治算法的适用条件

分治算法适用于满足以下 4 个条件的问题：

可分解：原问题能拆分为若干规模更小、结构相同的子问题。
子问题独立：各子问题互不影响，无重叠部分。
有终止条件：子问题足够小时可直接解决。
可合并：子问题的解能高效合并为原问题的解，且合并过程不能太复杂。

2. 分治算法的基本步骤

分治算法通常包括以下三个核心步骤：

分解：将原问题拆分为若干个规模更小、结构相同且相互独立的子问题。
求解：递归地解决每个子问题。
合并：将各子问题的解按照原问题的要求逐层合并，最终得到整体问题的解。

在第 $1$ 步分解时，建议将问题划分为规模尽量相等的 $k$ 个子问题，这样可以保持递归树的平衡，提升算法效率。实际应用中， $k = 2$ 是最常见的选择。子问题规模均衡，通常比不均衡的划分方式更优。

第 $2$ 步的递归求解，意味着对子问题继续应用相同的分治策略，直到子问题足够简单，可以直接用常数时间解决为止。

完成递归求解后，最小子问题的解可直接获得。随后，按照递归回归的顺序，自底向上逐步合并子问题的解，最终得到原问题的答案。

在实际编写分治算法时，代码结构也应严格遵循上述 $3$ 个步骤，便于理解和维护。伪代码如下：

def divide_and_conquer(problem_n):
    """
    分治算法通用模板
    :param problem_n: 问题规模
    :return: 原问题的解
    """
    # 1. 递归终止条件：当问题规模足够小时，直接解决
    if problem_n < d:  # d 为可直接求解的最小规模
        return solve(problem_n)  # 直接求解（注意：原代码有拼写错误，应为 solve）

    # 2. 分解：将原问题分解为 k 个子问题
    problems_k = divide(problem_n)  # divide 函数返回 k 个子问题的列表

    # 3. 递归求解每个子问题
    res = []
    for sub_problem in problems_k:
        sub_res = divide_and_conquer(sub_problem)  # 递归求解子问题
        res.append(sub_res)  # 收集每个子问题的解

    # 4. 合并：将 k 个子问题的解合并为原问题的解
    ans = merge(res)
    return ans  # 返回原问题的解

3. 分治算法分析

分治算法的核心在于：将大问题递归拆分为更小的子问题，直到子问题足够简单（通常可直接用常数时间解决），然后合并子问题的解。实际的时间复杂度主要由「分解」和「合并」两个过程决定。

一般情况下，分治算法会把原问题拆成 $a$ 个规模为 $n/b$ 的子问题，递归式为：

T(n) = \begin{cases} \Theta(1) & n = 1 \\ a \times T(n/b) + f(n) & n > 1 \end{cases}

其中， $a$ 表示子问题个数， $n/b$ 是每个子问题的规模， $f(n)$ 是分解和合并的总耗时。

求解分治算法复杂度，常用两种方法：递推法和递归树法。

3.1 递推法

以归并排序为例，其递归式为：

T(n) = \begin{cases} O(1) & n = 1 \\ 2T(n/2) + O(n) & n > 1 \end{cases}

递推展开如下：

\begin{aligned} T(n) &= 2T(n/2) + O(n) \\ &= 2[2T(n/4) + O(n/2)] + O(n) \\ &= 4T(n/4) + 2O(n/2) + O(n) \\ &= 4T(n/4) + O(n) + O(n) \\ &= 8T(n/8) + 3O(n) \\ &\dots \\ &= 2^x T(n/2^x) + xO(n) \end{aligned}

当 $n = 2^x$ ， $x = \log_2 n$ ，最终：

T(n) = n \cdot T(1) + \log_2 n \cdot O(n) = O(n \log n)

则归并排序的时间复杂度为 $O(n \log n)$ 。

3.2 递归树法

递归树法可以直观展示每层的分解和合并成本。以归并排序为例：

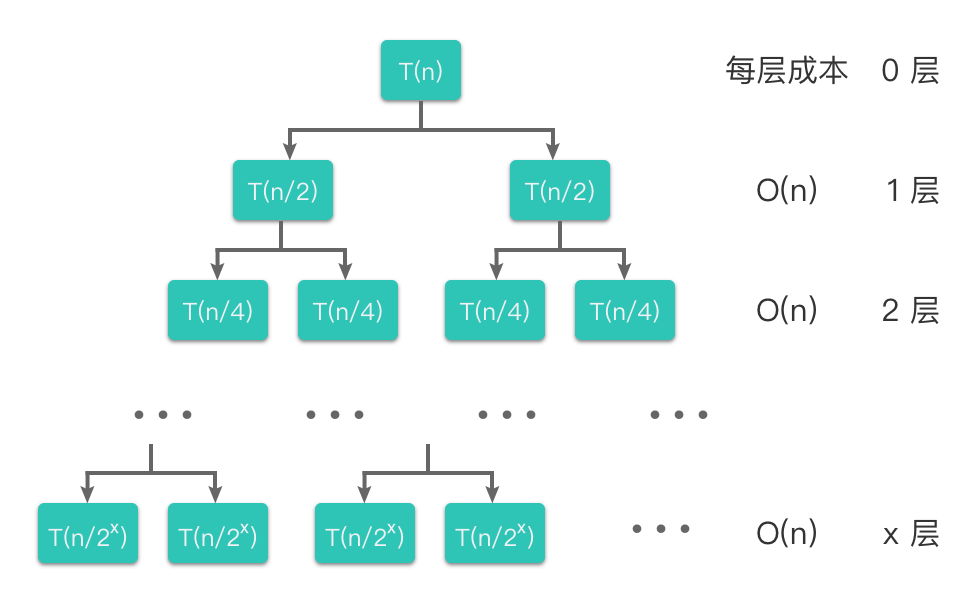
每层分解为 2 个子问题，总共 $\log_2 n$ 层。
每层合并的总耗时为 $O(n)$ 。

总复杂度为：

\begin{aligned} \text{总耗时} &= \underbrace{n \cdot O(1)}_{\text{叶子节点}} + \underbrace{O(n) \cdot \log_2 n}_{\text{每层合并}} \\ &= O(n) + O(n \log n) \\ &= O(n \log n) \end{aligned}

下图为归并排序的递归树示意：

4. 分治算法的应用

4.1 经典例题：归并排序

4.1.1 题目链接

912. 排序数组 - 力扣（LeetCode）

4.1.2 题目大意

描述：给定一个整数数组 $nums$ 。

要求：对该数组升序排列。

说明：

$1 \le nums.length \le 5 * 10^4$ 。
$-5 * 10^4 \le nums[i] \le 5 * 10^4$ 。

示例：

输入    nums = [5,2,3,1]
输出    [1,2,3,5]

4.1.3 解题思路

本题采用归并排序算法求解，其步骤如下：

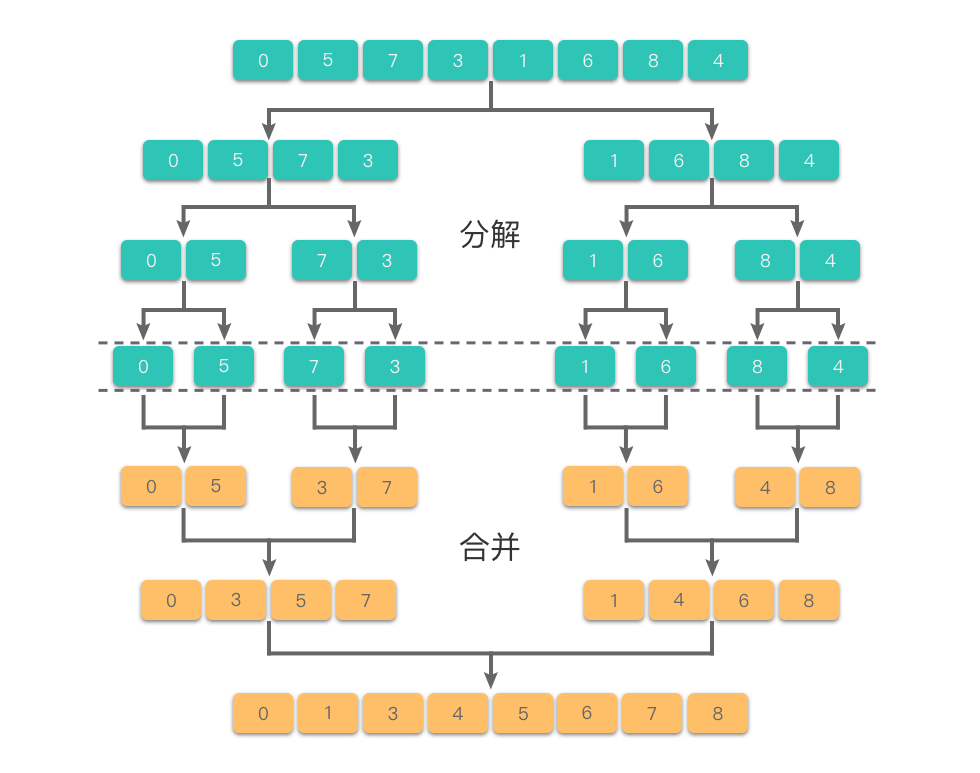
分解：将待排序数组递归地一分为二，分别划分为左右两个子数组，每个子数组大致包含 $\frac{n}{2}$ 个元素。
递归排序：对左右两个子数组分别递归进行归并排序，直到子数组长度为 $1$ ，此时视为有序。
合并：将两个有序子数组合并为一个有序数组，逐层向上合并，最终得到整体有序的结果。

下图展示了归并排序对数组排序的具体过程：

4.1.4 代码

class Solution:
    def merge(self, left_arr, right_arr):           # 合并
        arr = []
        while left_arr and right_arr:               # 将两个排序数组中较小元素依次插入到结果数组中
            if left_arr[0] <= right_arr[0]:
                arr.append(left_arr.pop(0))
            else:
                arr.append(right_arr.pop(0))
                
        while left_arr:                             # 如果左子序列有剩余元素，则将其插入到结果数组中
            arr.append(left_arr.pop(0))
        while right_arr:                            # 如果右子序列有剩余元素，则将其插入到结果数组中
            arr.append(right_arr.pop(0))
        return arr                                  # 返回排好序的结果数组

    def mergeSort(self, arr):                       # 分解
        if len(arr) <= 1:                           # 数组元素个数小于等于 1 时，直接返回原数组
            return arr
        
        mid = len(arr) // 2                         # 将数组从中间位置分为左右两个数组。
        left_arr = self.mergeSort(arr[0: mid])      # 递归将左子序列进行分解和排序
        right_arr =  self.mergeSort(arr[mid:])      # 递归将右子序列进行分解和排序
        return self.merge(left_arr, right_arr)      # 把当前序列组中有序子序列逐层向上，进行两两合并。

    def sortArray(self, nums: List[int]) -> List[int]:
        return self.mergeSort(nums)

4.2 经典例题：二分查找

4.2.1 题目链接

704. 二分查找 - 力扣（LeetCode）

4.2.2 题目大意

描述：给定一个含有 $n$ 个元素有序的（升序）整型数组 $nums$ 和一个目标值 $target$ 。

要求：返回 $target$ 在数组 $nums$ 中的位置，如果找不到，则返回 $-1$ 。

说明：

假设 $nums$ 中的所有元素是不重复的。
$n$ 将在 $[1, 10000]$ 之间。
$-9999 \le nums[i] \le 9999$ 。

示例：

输入    nums = [-1,0,3,5,9,12], target = 9
输出    4
解释    9 出现在 nums 中并且下标为 4

4.2.3 解题思路

本题采用分治思想进行求解。与典型的分治问题不同，二分查找无需对子问题的结果进行合并，最小子问题的解即为原问题的解。

具体步骤如下：

分解：将当前数组划分为左右两个子区间，每个子区间大致包含 $\frac{n}{2}$ 个元素。
处理：选取中间元素 $nums[mid]$ $n u m s [mi d]$ ，并与目标值 $target$ $t a r g e t$ 进行比较：
1. 如果 $nums[mid] == target$ ，则直接返回该元素下标；
2. 如果 $nums[mid] < target$ ，则在右侧子区间递归查找；
3. 如果 $nums[mid] > target$ ，则在左侧子区间递归查找。

下图展示了二分查找的分治过程。

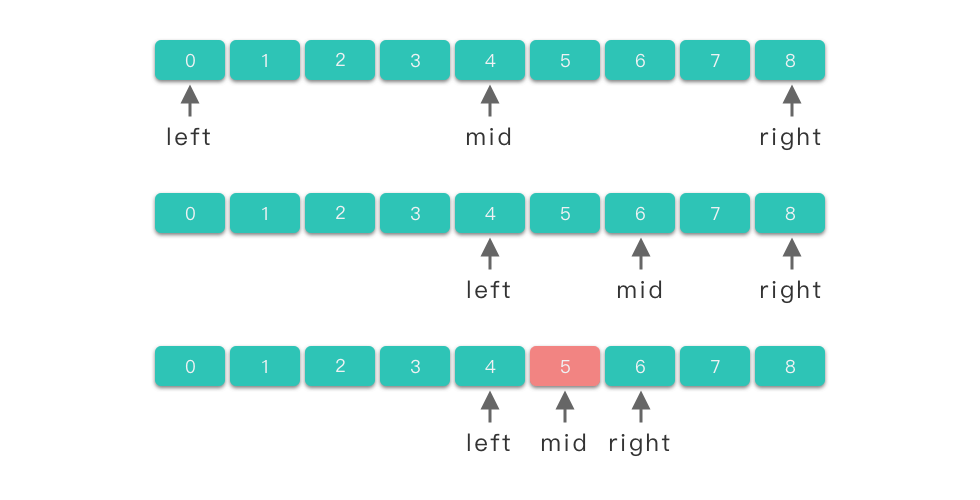
4.2.4 代码

二分查找问题的非递归实现的分治算法代码如下：

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left = 0
        right = len(nums) - 1
        # 在区间 [left, right] 内查找 target
        while left < right:
            # 取区间中间节点
            mid = left + (right - left) // 2
            # nums[mid] 小于目标值，排除掉不可能区间 [left, mid]，在 [mid + 1, right] 中继续搜索
            if nums[mid] < target:
                left = mid + 1 
            # nums[mid] 大于等于目标值，目标元素可能在 [left, mid] 中，在 [left, mid] 中继续搜索
            else:
                right = mid
        # 判断区间剩余元素是否为目标元素，不是则返回 -1
        return left if nums[left] == target else -1

5. 总结

分治是一种「拆分—求解—合并」的通用思维范式：将大问题拆为若干规模更小且相互独立的同构子问题，递归（或迭代）求解到足够小的基例，最后自底向上合并结果。是否适合分治，取决于子问题是否独立、规模能否尽量均衡、以及合并是否足够高效。

实践中要关注三个要点：

明确且正确的递归基与边界，避免无穷递归与越界；
尽量使子问题独立、规模均衡，必要时调整划分策略；
评估合并代价，若合并过重或子问题高度重叠，应考虑动态规划、记忆化或改用其他范式。

合理运用这些原则，分治能在排序、查找、几何与数值计算等领域提供简洁而高效的解法。

练习题目

参考资料

【书籍】趣学算法 - 陈小玉著
【书籍】算法之道 - 邹恒铭著
【书籍】算法图解 - 袁国忠译
【书籍】算法训练营陈小玉著
【博文】从合并排序算法看“分治法” - 船长&CAP - 博客园
【博文】递归、迭代、分治、回溯、动态规划、贪心算法 - 力扣
【博文】递归 & 分治 - OI Wiki
【博文】漫画：5分钟弄懂分治算法！它和递归算法的关系！